21

Лекция №3

Основные алгебраические операции над тензорами План

1. Линейные операции над тензорами, разложение по тензорным базисам.

2. Скалярное произведение тензоров одинаковых и различных рангов, свойства скалярного умножения, единичный тензор.

3. Тензор как линейный оператор, транспонированный тензор как сопряжённый оператор.

4. Билинейные и квадратичные формы симметричных тензоров.

1. Линейные операции над тензорами.

Рассматриваются две основные линейные операции – умножение тензоров на числа и сложение (вычитание) тензоров.

Умножение на число определяется как операция, при которой каждая из компонент тензора умножается на это число. Из определения следует, что данная операция инвариантна относительно изменения базиса. В результате данной операции ранг тензора не изменяется.

Для тензоров одинакового ранга вводится операция сложения (вычитания).

Тензор называется суммой (разностью) тензоров и , если его компоненты в некотором базисе равны сумме (разности) соответствующих (отнесённых к одной и той же базисной полиаде) компонент слагаемых тензоров. Например, для тензоров 2-го ранга, отнесённых к взаимному базису, связь между компонентами имеет следующий вид:

.

В инвариантной записи операция сложения определяется по формуле:

(3.1)

Очевидно, что операция сложения инвариантна относительно вектора базиса.

Наряду с операцией сложения тензоров рассмотрим операцию разложения по тензорным базисам. Ограничимся случаем тензоров 2-го ранга. Определим тензорный базис в : совокупность тензоров , где n 9, образует базис, если , не равных одновременно нулю выполняется следующее условие:

(3.2)

Множество тензоров , представляемое в виде

, n 9 (3.3)

образует n-мерное тензорное подпространство . Здесь - компоненты тензора .

Отметим, что в базис полного пространства тензоров 2-го ранга состоит по определению из девяти базисных диад - . Выражение (3.3) назовём разложением тензора по тензорному базису.

2. Скалярное умножение тензоров.

Ранее была введена операция скалярного умножения диад и полиад на вектор. Рассмотрим операцию скалярного умножения тензора на вектор. Пусть дан тензор 2-го ранга

(3.4)

Вводятся операции скалярного умножения тензора на вектор слева и справа. При правом умножении компоненты вектора скалярно умножаются на правые векторы базисных диад, входящих в сумму (3.4). Результат правого умножения имеет вид

(3.5)

Можно показать, что правая часть (3.5) есть вектор. Аналогичным образом определяется операция левого умножения

(3.6)

Из определений (3.5) и (3.6) следует, что векторы и в общем случае различны.

Отметим, что при скалярном умножении (3.5) и (3.6) перемножаются тензоры различных рангов, так как вектор есть тензор 1-го ранга. Операция скалярного умножения тензора ранга m на вектор определяется указанием номера векторов в базисных диадах, на которые скалярно умножаются вектора . Результат скалярного умножения тензора ранга m на вектор есть тензор ранга m-1.

Определим операцию скалярного умножения тензоров 2-го ранга. Будем называть тензор скалярным произведением тензора на тензор , если смешанные компоненты определяются следующими выражениями:

; (3.7)

; (3.8)

В диадном базисе представление (3.7) получается при скалярном умножении правых векторов взаимного диадного базиса тензора с базисными векторами тензора

(3.9)

Представлению (3.8) соответствует скалярное умножение правых векторов ковариантного базиса и левых векторов контравариантного базиса , тогда

(3.10)

Отметим, что представление одного из сомножителей в ковариантном, а другого в контравариантном базисах диктует простой способ записи конечного результата, так как . В общем случае можно относить перемножаемые тензоры и к другим базисам (основному, взаимному, смешанному), естественно, что результат при этом не изменяется. Например, относя оба вектора к основному базису, получим

(3.11)

Запись (3.11), в отличие от (3.9) и (3.10) включает компоненты метрического тензора.

Основным свойством скалярного умножения тензоров является его некоммутативность. То есть в общем случае

. (3.12)

Условие некоммутативности (3.12) получается непосредственно из сравнения компонент произведения. В частности, из (3.9) следует, что

.

Фундаментальную роль играет единичный тензор 2-го ранга - , который определяется из условия

(3.13)

Покажем, что единичный тензор совпадает с метрическим тензором. Представим тензоры и в смешанных базисах разложениями

; . (3.14)

Используя (3.14), условие (3.13) приводит к следующим уравнениям:

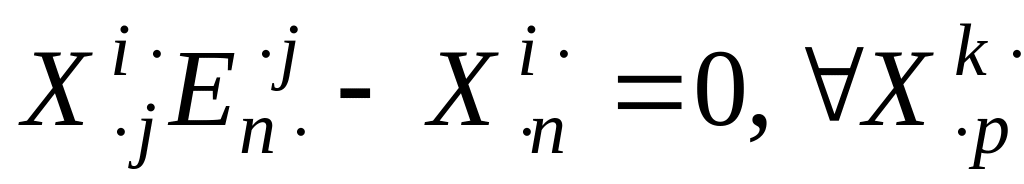(3.15)

Система (3.15) тождественно удовлетворяется, если

.

Таким образом, в смешанном базисе единичный тензор представляется единичной матрицей и его диадное разложение имеет вид

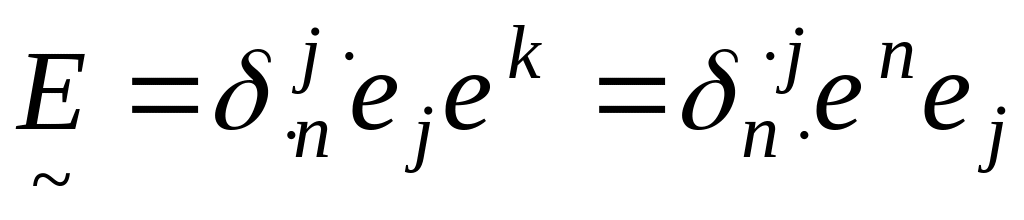(3.16)

Переходя на основании формул (1.7) и (1.8) к основному и взаимному базисам, получим

(3.17)

Из (3.17) следует, что единичный тензор совпадает с метрическим.

Непосредственной проверкой убеждаемся, что операция скалярного произведения ассоциативна и поэтому имеют место следующие выражения:

,

.