
- •15 Кафедра математического анализа
- •Глава 4. Элементы теории поля
- •§1. Скалярные и векторные поля. Поверхность уровня. Векторные линии
- •§2. Дивергенция и ротор векторного поля. Оператор Гамильтона
- •§3. Поток векторного поля
- •§4. Циркуляция векторного поля
- •§5. Потенциальные и соленоидальные поля
- •Задания для самостоятельного решения:
- •5. Вычислить поток векторного поля f через замкнутую поверхность в направлении внешней нормали, если:
- •6. Найти циркуляцию плоского векторного поля f вдоль кривой l (направление обхода – положительное):
- •7. Найти циркуляцию векторного поля f вдоль замкнутого контура l:
- •8. Являются ли следующие векторные поля потенциальными?
- •9. Показать, что следующие векторные поля потенциальны, и найти их потенциалы:
- •10. Являются ли следующие векторные поля соленоидальными?
§5. Потенциальные и соленоидальные поля
Векторное
поле F
называется потенциальным,
если оно является градиентом некоторого
скалярного поля U,
т.е. F
= grad
U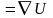 .
.
В случае если поле F потенциально, выполняются равенства
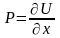 ,
,
 ,
,
 ,
,
что
равносильно тому, что выражение
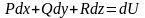 является полным дифференциалом некоторой
функции
.
Эта функция называется потенциалом
векторного поля F.
является полным дифференциалом некоторой
функции
.
Эта функция называется потенциалом
векторного поля F.
Теорема.
Пусть область
поверхностно односвязна и функции
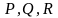 – непрерывно дифференцируемы в
.
Тогда векторное поле F
потенциально тогда и только тогда, когда
выполняются равенства:
– непрерывно дифференцируемы в
.
Тогда векторное поле F
потенциально тогда и только тогда, когда
выполняются равенства:
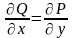 ,
,
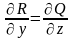 ,
,
 .
.
Приведенная теорема утверждает, что векторное поле F потенциально тогда и только тогда, когда rot F = 0, т.е. поле является безвихревым. Условие rot F = 0 является также необходимым и достаточным условием того, что криволинейный интеграл

не зависит от формы кривой, соединяющей точки А и В в области , а также того, что циркуляция поля F по любому замкнутому контуру равна нулю, т.е.
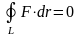 .
.
Если
поле F
потенциально, то его потенциал U
можно найти непосредственным
интегрированием по некоторому пути
 :
:
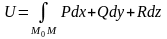 .
.
При
этом, в силу независимости этого интеграла
от формы пути, путь
выбирают в виде ломаной
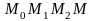 ,
вдоль каждого из звеньев которой
изменяется лишь одна координата, а
остальные остаются постоянными. В этом
случае два из трех дифференциалов в
криволинейном интеграле обращаются в
ноль, и потенциал вычисляется в виде
суммы:
,
вдоль каждого из звеньев которой
изменяется лишь одна координата, а
остальные остаются постоянными. В этом
случае два из трех дифференциалов в
криволинейном интеграле обращаются в
ноль, и потенциал вычисляется в виде
суммы:
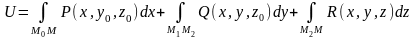 ,
,
где каждый из интегралов – есть обычный определенный интеграл по соответствующей переменной, а остальные переменные играют роль констант.
Если потенциал векторного поля F известен, то
 .
.
Векторное
поле F
называется соленоидальным,
если оно является ротором некоторого
векторного поля А,
т.е. F
rot
A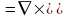 A.
Поле А
называется векторным
потенциалом
поля F.
A.
Поле А
называется векторным
потенциалом
поля F.
Теорема. Пусть область пространственно односвязна и координаты векторного поля непрерывно дифференцируемы в . Тогда векторное поле F соленоидально в том и только в том случае, когда
div
F
в каждой точке области .
Если векторное поле соленоидально, то его поток через любую замкнутую поверхность равен нулю.
Пример.
Показать, что поле F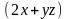 i
i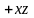 j
j k
потенциально и найти его потенциал.
k
потенциально и найти его потенциал.
Покажем, что rot F = 0.
rot
F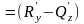 i
j
k
i
j
k i
i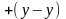 j
j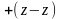 k
0.
k
0.
Следовательно, поле F потенциально. Найдем потенциал поля F непосредственным интегрированием.
Зафиксируем
точку
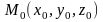 и рассмотрим произвольную точку
и рассмотрим произвольную точку
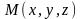 .
Тогда
.
Тогда
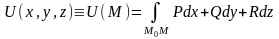 .
.
Линию
интегрирования (в силу независимости
такого интеграла от формы пути) выберем
в виде ломаной
,
где отрезок
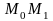 параллелен оси
,
отрезок
параллелен оси
,
отрезок
 – оси
,
а отрезок
– оси
,
а отрезок
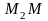 – оси
.
Вдоль
имеем
– оси
.
Вдоль
имеем
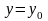 и
и
 ,
а, следовательно,
,
а, следовательно,
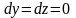 ,
вдоль
уже
,
вдоль
уже
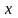 –
постоянно и
,
откуда
–
постоянно и
,
откуда
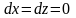 ,
а вдоль
обе переменные,
и
,
а вдоль
обе переменные,
и
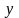 – постоянны, а, значит,
– постоянны, а, значит,
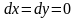 .
Тогда
.
Тогда
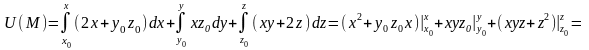
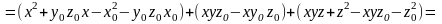
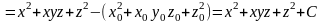 .
.
Контрольные вопросы:
Дайте определение потенциального векторного поля F.
Какие равенства выполняются, когда поле F потенциально?
Дайте определение соленоидального векторного поля F.
Приведите необходимое и достаточное условие того, что векторное поле F соленоидально.
