
§3. Поверхностный интеграл
Определение и вычисление поверхностного интеграла первого рода
Пусть
в точках некоторой гладкой поверхности
S
определена ограниченная функция
.
Разобьем поверхность S
произвольно на п
частей с площадями
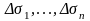 и диаметрами
и диаметрами
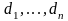 соответственно. Выбираем на каждой
частичной поверхности произвольную
точку
соответственно. Выбираем на каждой
частичной поверхности произвольную
точку
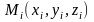 ,
составляем сумму
,
составляем сумму

которая называется интегральной суммой первого рода для функции .
Обозначим
через
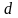 наибольший из диаметров частей
поверхностей. Если при
существует предел интегральных сумм,
который не зависит от способа разбиения
поверхности S
на части и выбора точек
,
то предел называется поверхностным
интегралом первого рода и
обозначается
наибольший из диаметров частей
поверхностей. Если при
существует предел интегральных сумм,
который не зависит от способа разбиения
поверхности S
на части и выбора точек
,
то предел называется поверхностным
интегралом первого рода и
обозначается
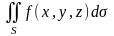 .
.
Если функция непрерывна, то интеграл
существует.
Определение поверхностного интеграла первого рода аналогично определению криволинейного интеграла первого рода. Свойства поверхностного интеграла первого рода (линейность, аддитивность) также аналогичны соответствующим свойствам криволинейного интеграла первого рода.
Если
поверхность S
задана на области
плоскости
функцией
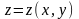 ,
причем
,
причем
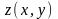 непрерывна вместе со своими частными
производными
непрерывна вместе со своими частными
производными
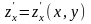 ,
,
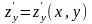 ,
то поверхностный интеграл сводится к
двойному с помощью формулы:
,
то поверхностный интеграл сводится к
двойному с помощью формулы:
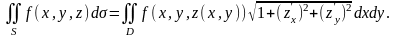
Если
поверхность S
задана параметрически в виде
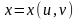 ,
,
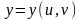 ,
,
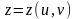 ,
где
,
где
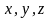 - непрерывно дифференцируемые функции
в некоторой области
- непрерывно дифференцируемые функции
в некоторой области
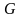 плоскости
плоскости
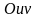 ,
то
,
то
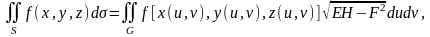
где
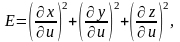

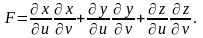
Приложения поверхностного интеграла первого рода
Пусть
S
– материальная поверхность с плотностью
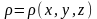 .
Тогда с помощью поверхностных интегралов
можно вычислить:
.
Тогда с помощью поверхностных интегралов
можно вычислить:
1) статические моменты этой поверхности относительно координатных плоскостей
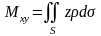 ,
,
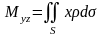 ,
,
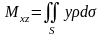 ;
;
2) координаты центра тяжести поверхности
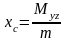 ,
,
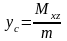 ,
,
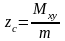 ,
где
,
где
 ;
;
3) моменты инерции относительно координатных осей и начала координат

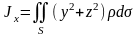 ,
,
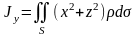 ,
,
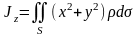 ,
,
 .
.
Определение и вычисление поверхностного интеграла второго рода
Пусть
- гладкая ориентированная поверхность,
на которой задана непрерывная функция
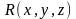 ,
и пусть в каждой точке
поверхности определено положительное
направление нормали
,
и пусть в каждой точке
поверхности определено положительное
направление нормали
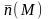 (
- непрерывная вектор – функция).
(
- непрерывная вектор – функция).
Выберем
ту сторону
 поверхности
,
для которой угол между единичной нормалью
поверхности
,
для которой угол между единичной нормалью
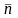 и осью
острый. Теперь разобьем поверхность
на части
и осью
острый. Теперь разобьем поверхность
на части
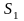 ,
…,
с диаметрами
,
…,
с диаметрами
![]() ,
…,
,
…,
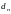 .
Обозначим через
.
Обозначим через
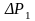 ,
…,
,
…,
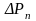 площади соответствующих проекций частей
,
…,
на плоскость
,
а через
- максимум из чисел
,
…,
площади соответствующих проекций частей
,
…,
на плоскость
,
а через
- максимум из чисел
,
…,
.
Выбрав в каждой части
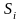 произвольную точку
,
составим сумму
произвольную точку
,
составим сумму

которая называется интегральной суммой второго рода для функции . Предел интегральных сумм (он существует в силу непрерывности ) при , не зависящий от способа разбиения поверхности на части и выбора точек , называется поверхностным интегралом второго рода от функции по поверхности и обозначается
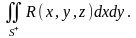
Аналогично определяются поверхностные интегралы второго рода
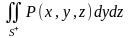 и
и
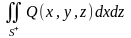
от
непрерывных функций
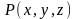 и
и
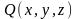 .
Сумма трех указанных поверхностных
интегралов второго рода называется
общим
поверхностным интегралом второго рода
и
обозначается
.
Сумма трех указанных поверхностных
интегралов второго рода называется
общим
поверхностным интегралом второго рода
и
обозначается

Пусть
теперь поверхность
имеет явно представление
,
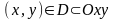 .
Тогда поверхностный интеграл второго
рода сводится к двойному интегралу по
области
.
Тогда поверхностный интеграл второго
рода сводится к двойному интегралу по
области
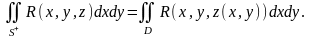
Если
выбрана противоположная сторона
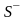 поверхности
,
то
поверхности
,
то
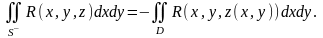
Аналогично вычисляются и поверхностные интегралы
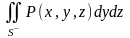 и
и
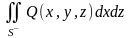 .
.
Связь поверхностных интегралов первого и второго рода
Если
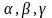 - углы, образованные соответственно с
положительными направлениями осей
,
и
,
единичной нормалью n
к выбранной стороне
поверхности S,
тогда связь поверхностных интегралов
первого и второго рода выражается
следующим равенством
- углы, образованные соответственно с
положительными направлениями осей
,
и
,
единичной нормалью n
к выбранной стороне
поверхности S,
тогда связь поверхностных интегралов
первого и второго рода выражается
следующим равенством

Поскольку
n
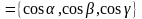 ,
то
поверхностный интеграл первого рода в
правой части этого равенства можно
записать компактно в векторной форме
,
то
поверхностный интеграл первого рода в
правой части этого равенства можно
записать компактно в векторной форме
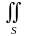 F·n
F·n
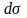 ,
,
где
F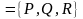 - векторное
поле, определенное на S.
- векторное
поле, определенное на S.
Векторное поле F можно ассоциировать с полем скоростей жидкости, протекающей через поверхность S. Тогда интеграл
F·n
можно истолковывать механически как общее количество жидкости, протекающее в единицу времени через поверхность в положительном направлении, т. е. вдоль n. Поэтому этот интеграл называется потоком векторного поля F через поверхность .
Пример 1. Вычислить поверхностный интеграл первого рода
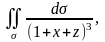
где
у – часть плоскости
 ,
заключенная в первом октанте.
,
заключенная в первом октанте.

Рис. 36.
Поверхность
у можно выразить явно:
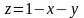 ,
,
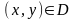 ,
где область
- треугольник, ограниченный прямыми
,
и
,
где область
- треугольник, ограниченный прямыми
,
и
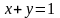 (рис. 36). При этом
(рис. 36). При этом
 Данный интеграл сводится к двойному
(при этом знаменатель подынтегральной
функции равен
Данный интеграл сводится к двойному
(при этом знаменатель подынтегральной
функции равен
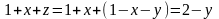 ):
):
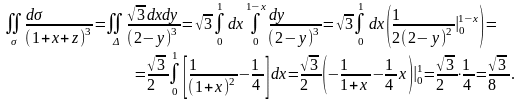
Пример 2. Вычислить поверхностный интеграл первого рода
 ,
,
где
у – сфера
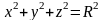 .
.
В
силу симметрии относительно координатных
плоскостей поверхности у и подынтегральной
функции ограничимся вычислением
интеграла при условии
,
,
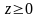 ,
а результат умножим на 8.
,
а результат умножим на 8.
Используя
сферические координаты, запишем
параметрические уравнения сферы
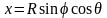 ,
,
 ,
,
 ,
учитывая, что
,
учитывая, что
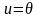 ,
,
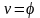 .
Тогда
.
Тогда
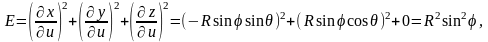
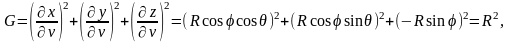
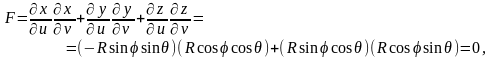
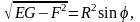
а
область интегрирования – четверть
круга
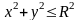 в параметрической форме имеет вид
в параметрической форме имеет вид
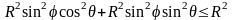 ,
,
,
,
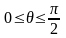 .
.
Остается
выразить через параметры подынтегральную
функцию
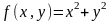 .
На сфере
имеем
.
На сфере
имеем
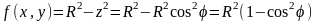 .
Таким образом данный интеграл равен
.
Таким образом данный интеграл равен

Пример 3. Вычислить поверхностный интеграл второго рода
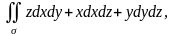
где у – внешняя поверхность плоскости , ограниченной координатными плоскостями.
Интеграл будем вычислять покомпонентно, проектируя у на разные координатные плоскости (рис. 37).
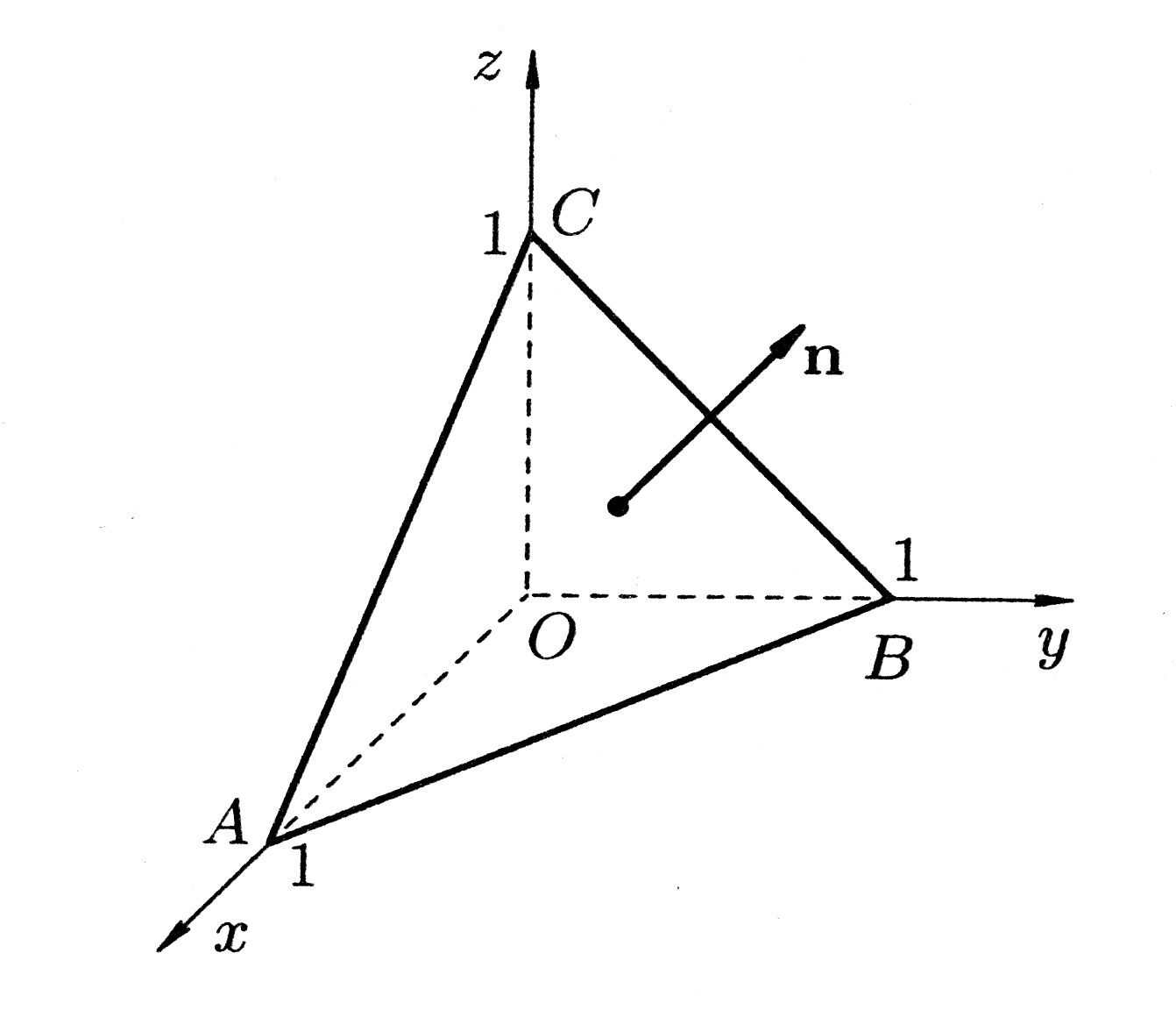
Рис. 37.
Вычислим

Выражая
явно
 через
и
через
и
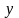 ,
сведем этот интеграл к двойному интегралу
по
,
сведем этот интеграл к двойному интегралу
по
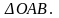 Подставляя
в подынтегральную функцию и учитывая,
что:
,
Подставляя
в подынтегральную функцию и учитывая,
что:
,
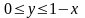 ,
получаем
,
получаем
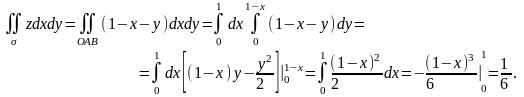
Остальные интегралы
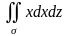 и
и
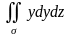
приводят
к такому же результату. Поэтому искомый
интеграл равен
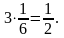
Пример
4.
Найти поток векторного поля F(x,
y,
z)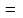 xi
+ yj
+zk
через часть поверхности эллипсоида
xi
+ yj
+zk
через часть поверхности эллипсоида
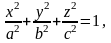
лежащую в первом октанте в направлении внешней нормали.
Искомый поток равен
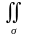 F·n
=
F·n
=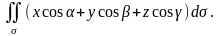
Последний интеграл сводится к поверхностным интегралам второго рода

где
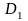 ,
,
 ,
,
 - проекции эллипсоида на соответствующие
координатные плоскости.
- проекции эллипсоида на соответствующие
координатные плоскости.
Рассмотрим, например,

где можно выразить через и из уравнения эллипсоида, - внутренность четверти эллипса
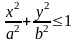 ,
,
.
,
,
.
Очевидно, что
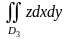
равен
объему восьмой части эллипсоида, которая,
как известно, равна
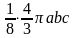 .
Аналогично находим и другие интегралы,
отсюда получаем, что исходный интеграл
первого рода, т. е. поток векторного
поля, равен
.
Аналогично находим и другие интегралы,
отсюда получаем, что исходный интеграл
первого рода, т. е. поток векторного
поля, равен
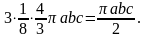
Пример
5.
Найти поток вектора F
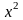 i
i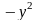 j
j![]() k
через поверхность тела, ограниченного
сферой
k
через поверхность тела, ограниченного
сферой
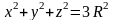 ,
плоскостью
и однополостным гиперболоидом
,
плоскостью
и однополостным гиперболоидом
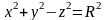 .
.
Имеем
F·n

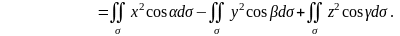
На плоскости и поверхность у проектируется дважды, с обеих сторон, к тому же поверхность у симметрична относительно этих плоскостей. Поэтому соответствующие интегралы получаются нулевыми:
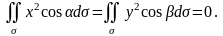
А теперь вычислим
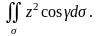
Поверхность у состоит из трех частей (рис. 38):

Рис. 38.
а)
сегмент сферы
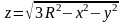 ,
для которого
,
для которого
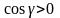 (внешняя нормаль образует с
острый угол); проекция этого сегмента
на
есть круг
(внешняя нормаль образует с
острый угол); проекция этого сегмента
на
есть круг
 (сегмент
сферы
пересекается
с гиперболоидом
по линии
(сегмент
сферы
пересекается
с гиперболоидом
по линии
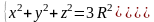 —
—
окружность
радиуса
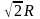 );
);
б)
сегмент параболоида проектируется на
в кольцо
 ,
,
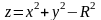 (из уравнения гиперболоида);
(из уравнения гиперболоида);
в)
третья часть – это круг
,
на котором
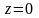 .
.
Поэтому
F·n
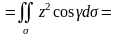
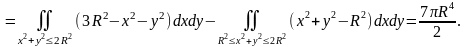
Пример
6. Найти
массу полусферы
,
радиуса
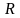 с поверхностной плотностью, равной
с поверхностной плотностью, равной
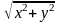 .
.
Имеем
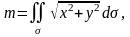
где
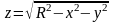 ,
,
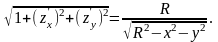
Следовательно,
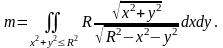
Переходя к полярным координатам в двойном интеграле, получаем

Контрольные вопросы:
Дайте определение поверхностного интеграла первого рода.
Дайте определение поверхностного интеграла второго рода.
Приведите формулу для вычисления статических моментов поверхности относительно координатных плоскостей.
Приведите формулу для вычисления моментов инерции относительно координатных осей и начала координат.
В чем заключается связь поверхностных интегралов первого и второго рода?
