
25 Кафедра математического анализа
Методические указания по математике для самостоятельной работы студентов специальности «Геология»
Глава 3. Криволинейные и поверхностные интегралы
§1. Криволинейный интеграл первого рода
Определение криволинейного интеграла первого рода
Рассмотрим
на плоскости
 некоторую гладкую кривую
некоторую гладкую кривую

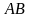 ,
предположим, что функция
,
предположим, что функция
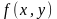 определена на кривой
.
Разобьем кривую
на п
произвольных частей точками
определена на кривой
.
Разобьем кривую
на п
произвольных частей точками
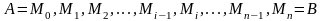 ,
выберем на каждой из частичных дуг
,
выберем на каждой из частичных дуг
 произвольную точку
произвольную точку
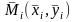 и составим сумму
и составим сумму

где
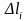 - длина дуги
.
Полученная сумма называется интегральной
суммой первого рода
для функции
,
заданной на кривой
.
- длина дуги
.
Полученная сумма называется интегральной
суммой первого рода
для функции
,
заданной на кривой
.
Обозначим
через d
наибольшую из длин дуг
,
т. е.
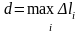 .
Если при
.
Если при
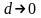 существует предел интегральных сумм
существует предел интегральных сумм
 (не зависящий от способа разбиения
кривой
на части и выбора точек
(не зависящий от способа разбиения
кривой
на части и выбора точек
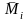 ),
то этот предел называется криволинейным
интегралом первого рода
от функции
по кривой
и обозначается
),
то этот предел называется криволинейным
интегралом первого рода
от функции
по кривой
и обозначается
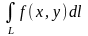 или
или
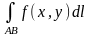 .
.
Криволинейный интеграл первого рода обладает теми же свойствами, что и определенный интеграл (аддитивность, линейность, оценка модуля, теорема о среднем). Но есть отличие:
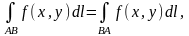
т. е. криволинейный интеграл первого рода не зависит от направления интегрирования.
Вычисление криволинейных интегралов первого рода
Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла. А именно:
1.
Если кривая
 задана непрерывно дифференцируемой
функцией
задана непрерывно дифференцируемой
функцией
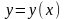 ,
,
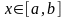 ,
то
,
то
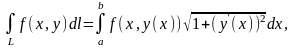
при
этом выражение
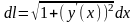 называется дифференциалом длины дуги.
называется дифференциалом длины дуги.
2.
Если кривая L
задана параметрически, т. е. в виде
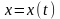 ,
,
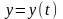 ,
где
,
где
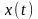 ,
,
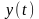 - непрерывно дифференцируемые функции
на некотором отрезке
- непрерывно дифференцируемые функции
на некотором отрезке
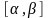 ,
то
,
то
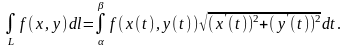
Это
равенство распространяется на случай
пространственной кривой
,
заданной параметрически:
,
,
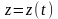 ,
,
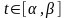 .
В этом случае, если
.
В этом случае, если
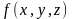 - непрерывная функция вдоль кривой
,
то
- непрерывная функция вдоль кривой
,
то
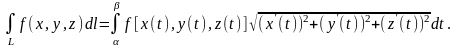
3.
Если плоская кривая
задана полярным уравнением
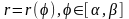 ,
то
,
то
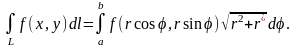
Приложения криволинейного интеграла первого рода
1. Если подынтегральная функция равна единице, то криволинейный интеграл
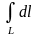
равен
длине
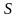 кривой
,
т. е.
кривой
,
т. е.
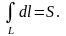
2.
Пусть в плоскости
задана гладкая кривая
,
на которой определена и непрерывна
функция двух переменных
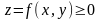 .
Тогда можно построить цилиндрическую
поверхность с направляющей
и образующей, параллельной оси
.
Тогда можно построить цилиндрическую
поверхность с направляющей
и образующей, параллельной оси
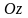 и заключенной между
и поверхностью
и заключенной между
и поверхностью
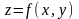 .
Площадь этой цилиндрической поверхности
можно вычислить по формуле
.
Площадь этой цилиндрической поверхности
можно вычислить по формуле
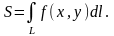
3.
Если
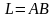 - материальная кривая с плотностью,
равной
- материальная кривая с плотностью,
равной
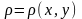 ,
то масса этой кривой вычисляется по
формуле
,
то масса этой кривой вычисляется по
формуле
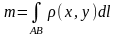 .
.
4.
Статические моменты материальной кривой
относительно координатных осей
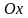 и
и
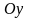 соответственно равны
соответственно равны
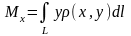 ,
,
 ,
,
где
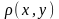 - плотность распределения кривой
,
а
- плотность распределения кривой
,
а
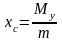 ,
,
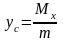 - координаты центра тяжести (центра
масс) кривой
.
- координаты центра тяжести (центра
масс) кривой
.
5. Интегралы
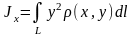 ,
,
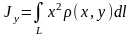 ,
,
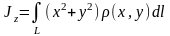
выражают моменты инерции кривой с линейной плотностью относительно осей , и начала координат соответственно.
Пример 1. Вычислить криволинейный интеграл
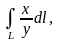
где
- дуга параболы
 ,
заключенная между точками
,
заключенная между точками
 и (8,4).
и (8,4).
Найдем
дифференциал дуги
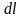 для кривой
для кривой
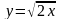 .
Имеем
.
Имеем
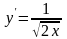 ,
,
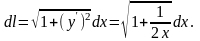
Следовательно, данный интеграл равен
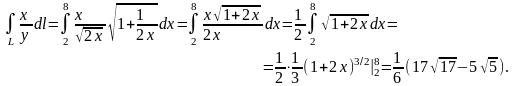
Пример 2. Вычислить криволинейный интеграл
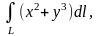
где
- контур треугольника
 с вершинами
с вершинами
 ,
,
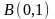 ,
,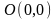 (рис. 30).
(рис. 30).
Поскольку
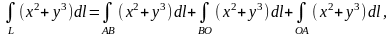
то
остается вычислить криволинейный
интеграл по каждому из отрезков
,
 и
и
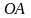 :
:
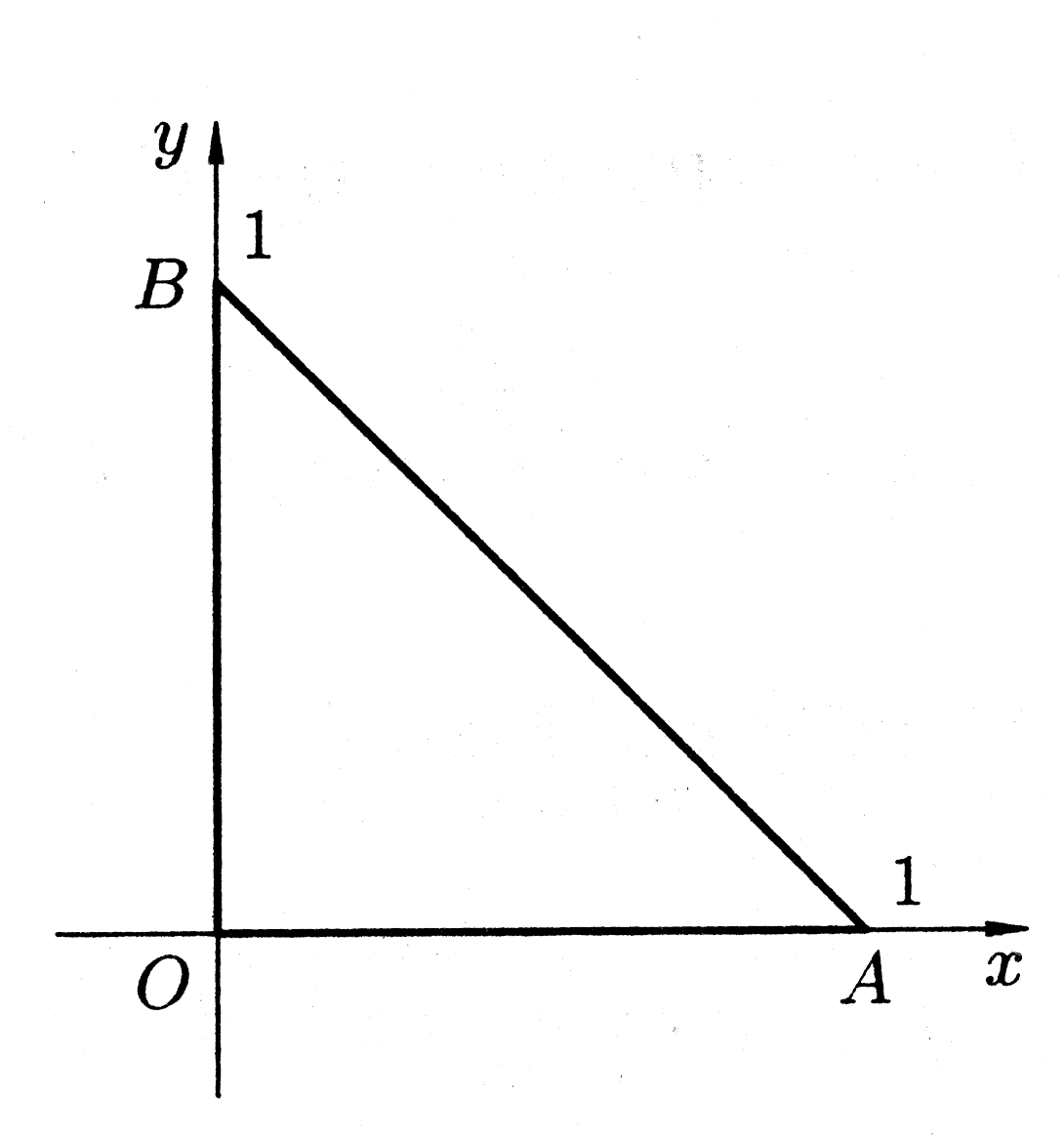
Рис. 30.
1)
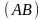 :
так как уравнение прямой
имеет вид
:
так как уравнение прямой
имеет вид
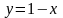 ,
то
,
то

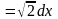 .
Учитывая, что
.
Учитывая, что меняется от 0 до 1, получим
меняется от 0 до 1, получим
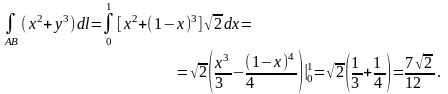
2)
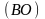 :
рассуждая аналогично, находим
:
рассуждая аналогично, находим
 ,
,
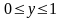 ,
,
![]() ,
откуда
,
откуда
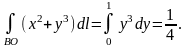
3)
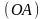 :
:
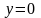 ,
,
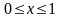 ,
,
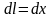 .
.
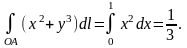
4) Окончательно
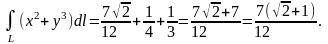
Пример 3. Вычислить криволинейный интеграл
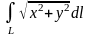 ,
,
где
- окружность
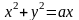 (а>0).
(а>0).
Введем
полярные координаты
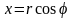 ,
,
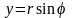 .
Тогда, поскольку
.
Тогда, поскольку
 ,
уравнение окружности примет вид
,
уравнение окружности примет вид
 ,
т.е.
,
т.е.
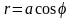 ,
а дифференциал дуги
,
а дифференциал дуги
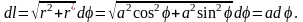
При
этом
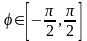 .
Следовательно,
.
Следовательно,
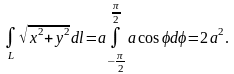
Пример 4. Вычислить криволинейный интеграл первого рода от функции с тремя переменными

где
- дуга кривой, заданной параметрически
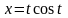 ,
,
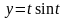 ,
,
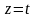 ,
,
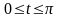 .
.
Перейдем
в подынтегральном выражении к переменной
 .
Имеем для подынтегральной функции:
.
Имеем для подынтегральной функции:
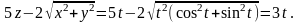
Теперь выразим через дифференциал :
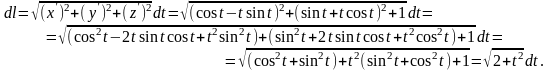
Таким образом,
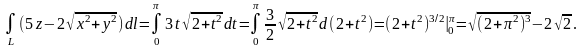
Пример
5.
Вычислить площадь части боковой
поверхности кругового цилиндра
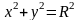 ,
ограниченной снизу плоскостью
,
а сверху поверхностью
,
ограниченной снизу плоскостью
,
а сверху поверхностью
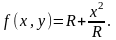
Искомая площадь вычисляется по формуле
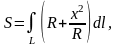
где
- окружность
.
Поверхность цилиндра и поверхность
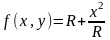 симметричны относительно координатных
плоскостей
симметричны относительно координатных
плоскостей
 и
и
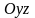 ,
поэтому можно ограничиться вычислением
интеграла при условиях
,
поэтому можно ограничиться вычислением
интеграла при условиях
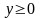 ,
,
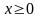 ,
т. е. вычислить четверть искомой площади.
Имеем
,
т. е. вычислить четверть искомой площади.
Имеем
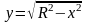 ,
,
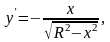
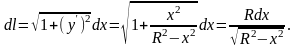
Следовательно,
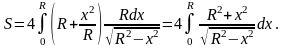
Получим
определенный интеграл, который вычисляем
с помощью подстановки
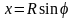 ,
откуда
,
откуда
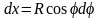 ,
,
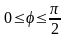 ,
,
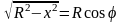 .
.
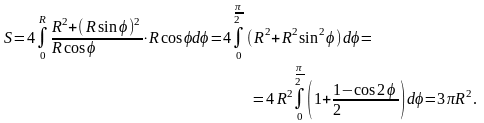
Пример
6. Вычислить
массу и координаты центра тяжести
однородной дуги циклоиды
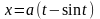 ,
,
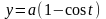 ,
,
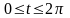 .
.
Имеем , , где
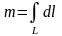 ,
,
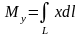 ,
,
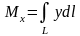 .
.
Находим
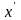 ,
,
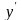 и
по отдельности:
и
по отдельности:
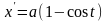 ,
,
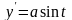 ,
,
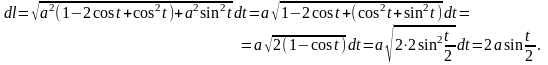
Следовательно,
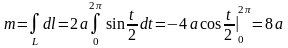 .
.
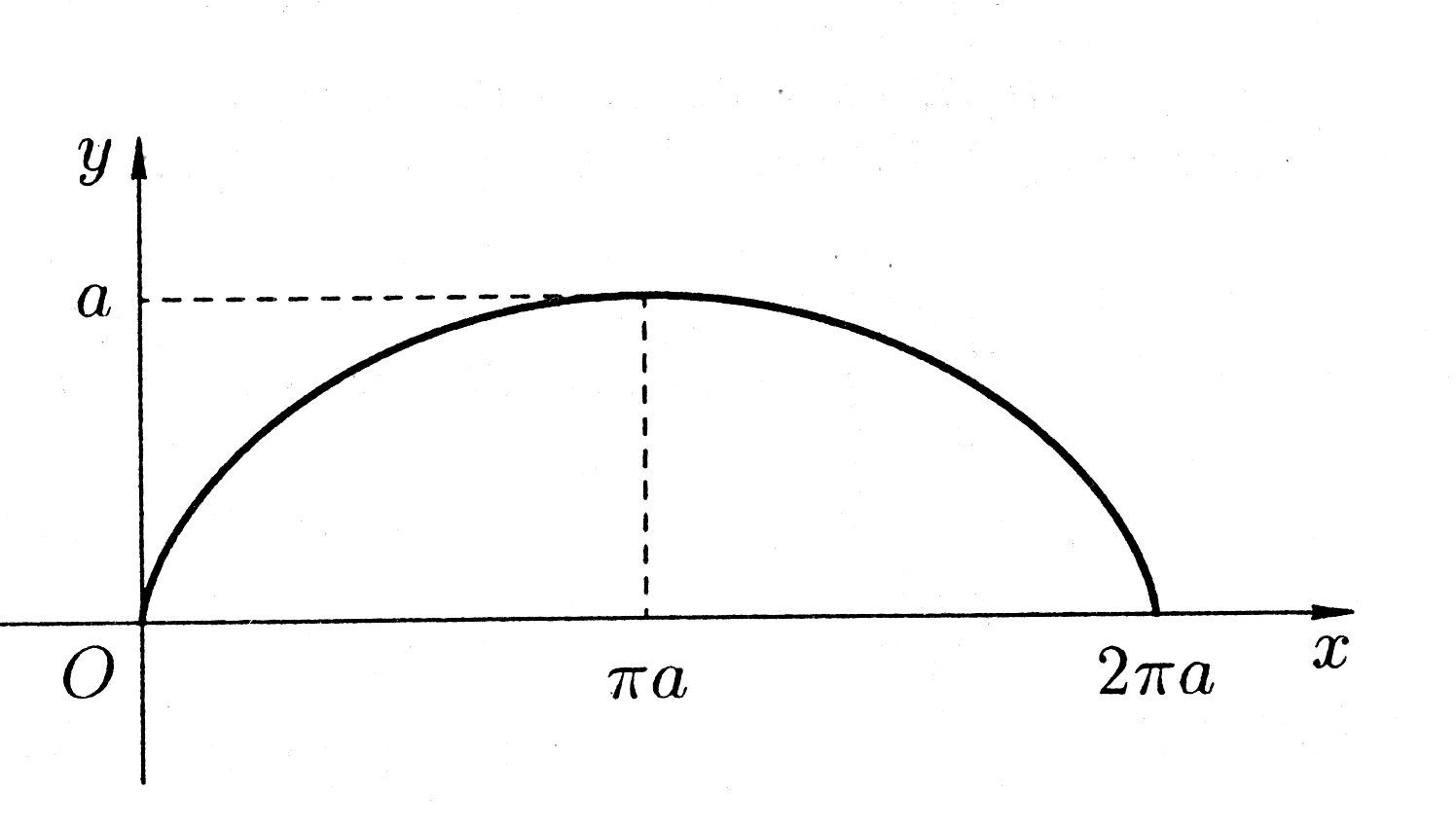
Рис. 31.
Из
рис. 31 видно, что циклоида симметрична
относительно прямой
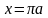 ,
поэтому
,
поэтому
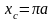 .
Таким образом, учитывая равенство
.
Таким образом, учитывая равенство
,
получаем,
что
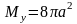 .
Вычислим теперь
.
Вычислим теперь
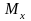 :
:

Окончательно получаем:
 ,
,
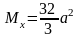 ,
,
,
,
,
,
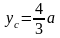 .
.
Пример
7.
Найти моменты инерции относительно
координатных осей и начала координат
четверти окружности
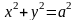 ,
,
.
Плотность распределения масс дуги
постоянна и равна
,
,
.
Плотность распределения масс дуги
постоянна и равна
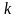 .
.
Данная
кривая (четверть окружности) симметрична
относительно биссектрисы
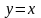 первого координатного угла. Тогда
первого координатного угла. Тогда
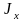 и
и
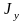 одинаковы, т.е.
одинаковы, т.е.
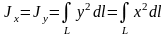 .
.
Переходя
к параметрическим уравнениям окружности
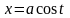 ,
,
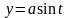 ,
,
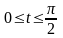 ,
откуда
,
откуда
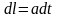 ,
получаем
,
получаем

Таким
образом
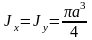 ,
,

Контрольная работа:
Дайте определение криволинейного интеграла первого рода от функции по кривой АВ.
Зависит ли криволинейный интеграл первого рода от пути интегрирования?
Приведите формулу для вычисления криволинейного интеграла по кривой, заданной параметрическими уравнениями?
Приведите формулу для вычисления массы кривой с плотностью .
Приведите формулу для вычисления статического момента кривой относительно оси Ох.
