§ 2.6 Целочисленное программирование. Графический метод. Метод Гомори Целочисленное программирование

Математическая задача целочисленного программирования в канонической форме формулируется следующим образом: найти такие целые неотрицательные значения х₁ , х₂ , х₃ , . . . , х_n , которые обеспечивают оптимальное (минимальное или максимальное) значение линейной функции (целевой функции)

W=

и удовлетворяют системе ограничений

Формулировка задачи совпадает с задачей линейного программирования, в которой добавлено ограничение на целочисленность оптимального решения.

Графический метод

Если математическая модель задачи целочисленного программирования имеет два параметра управления, и система ограничений представляет собой систему неравенств, то задача, аналогично задаче линейного программирования, может быть решена графически, с той особенностью, что областью допустимых решений будет не выпуклая область, а ее подмножество точек с целыми координатами.

Пример. Контейнер объемом 4,9м³ помещен на контейнеровоз грузоподъемностью 18т. Контейнер требуется заполнить грузом двух наименований. Масса единицы груза m_j (в тоннах), объем единицы груза V_j (в м³), стоимости с_j (в условных денежных единицах) приведены в таблице. Требуется загрузить контейнер таким образом, чтобы стоимость перевозимого груза была максимальной.

Вид груза j	mj	Vj	cj
1	4	0,7	10
2	3	1	11

Составим математическую модель задачи.

1. Критерием эффективности является стоимость перевозимого груза, стремящаяся к максимуму.

2. Параметрами управления являются х₁ – количество изделий первого типа; х₂ – количество изделий второго типа. Из условия следует, что параметры управления могут принимать только целые значения.

3. Составим систему ограничений: ограниченными являются грузоподъемность и объем контейнера. Из условия следует, что 4х₁ – масса всего груза первого типа, а 3х₂ – масса груза второго типа, тогда ограничение на грузоподъемность имеет вид:

.

Аналогично, ограничение на объем контейнера имеет вид:

.

Итак, система ограничений имеет вид:

4. Целевая функция – стоимость стремится к максимуму на системе ограничений.

5. Так как математическая модель содержит два параметра управления, задача может быть решена графически.

Найдем область допустимых решений системы ограничений, решив каждое из неравенств. В связи с целочисленностью решения впишем в ОДР «многоугольник» с углами в точках, имеющих целые координаты (рис. 3.8).

Построим градиент целевой функции gradW=(1,1;1) и опорную прямую L, приравняв целевую функцию к нулю:

Н

айдем точку «выхода» из области допустимых решений, если бы задача не требовала целого решения, то точкой «выхода» являлась бы точка А – пересечение границ (1) и (2) полуплоскостей. Однако, целочисленность изменяет вид ОДР, и точкой «выхода» из ступенчатой области допустимых решений будет точка В (3;2), которая не является соседней для точки А (рис. 3.8).

Найдем значение целевой функции в точке В(3;2):

W(3;2) = 1,13 + 2 = 5,3д.е.

Для сравнения найдем значения целевой функции в соседних точках (2; 3) и (1; 4).

W(2;3) = 1,12 + 3 = 5,2д.е.

W(1;4) = 1,11 + 4 = 5,1д.е.

Итак, для оптимального заполнения контейнера необходимо перевозить 3 единицы груза первого типа и две единицы второго.

Метод Гомори

В общем случае решения задач целочисленного программирования используют метод, называемый методом Гомори. Он является аналогом симплекс-метода, однако в нем добавляются дополнительные ограничения на целую и дробную части элементов матрицы системы.

Целой частью числа а называется наибольшее целое число, не превосходящее число а. Обозначают [a]. Например [1,5]=1; [–1,5]= –2.

Дробной частью числа называется разность между числом и его целой частью: {a}= a – [a]. Например, {2,1}= 2,1 – [2,1]=0,1;

{–2,1}= –2,1 – [–2,1]= –2,1– (–3) = 0,9.

Алгоритм решения задачи целочисленного программирования методом Гомори.

1. Задача решается симплекс-методом. Если решения получились целые, то никаких дополнительных ограничений не требуется.

2. Если же решение содержит хотя бы одну дробную компоненту, то в систему ограничений включается дополнительное ограничение для i-ой строки матрицы, в которой свободный член имеет наибольшую дробную часть:

(3.13)

здесь {a_ij} – дробные части всех элементов i-ой строки матрицы.

3. С новым ограничение задача продолжает решаться симплекс-методом, до нахождения оптимального решения, затем, если оно не целочисленное, повторяется п.2 и п.3 и т.д.

Покажем применение этого метода на примере.

Имеется достаточно большое количество бревен длиной 4м. Бревно следует распилить на заготовки двух видов 1,5 м и 1м, причем заготовок каждого типа должно быть получено не менее 50 и 90 шт. соответственно. Найдите наименьшее необходимое число бревен.

Составим математическую модель задачи.

1. Критерием эффективности является количество бревен, стремящееся к минимуму.

2. Бревно можно распилить несколькими способами:

Способ распилки	Бревно (4м)
	Заготовка 1,5м	Заготовка 1м
I	0	4
II	1	2
III	2	1
Необходимо всего	50	90

Примем за параметры управления количества бревен, распиленных тем или иным способом: х₁ – количество бревен, распиленных I способом; х₂ – II способом; х₃ – III способом. Параметры управления могут принимать только целые значения.

3. По таблице составим систему ограничений на количество заготовок: заготовка 1, 5 метра получается при распилке II и III способом.

.

Заготовка 1 метр получается при распилке всеми способами.

.

4. Целевая функция – количество бревен стремится к минимуму на системе ограничений.

5. Приведем систему к каноническому виду, так как оба неравенства содержат знак больше или равно, для того, чтобы заменить их на равенства, необходимо из левой части вычесть переменные х₄ и х₅, играющие роль излишков заготовок:

Решим задачу симплексным методом.

Составим матрицу системы и выберем базисные переменные.

.

В качестве первой базисной переменной можно выбрать либо х₂ либо х₃, так как соответствующие коэффициенты в первой строке положительны, составим соотношения (3.8) для этих столбцов:

.

Для третьего столбца минимум относится к первой строке, значит первая базисная переменная х₃.

Разделим первую строку на 2 и затем вычтем ее из второй строки. Второй базисной переменной выберем х₁.

Для приведения первого столбца к виду (0; 1) разделим вторую строку на 4.

.

Проверим, будет ли получившийся план оптимальным, составим симплекс таблицу.

CjСj	Б	1	1	1	0	0
		х1	х2	x3	х4	х5	bi
1	х3	0	0,5	1	–0,5	0	25
1	х1	1		0		–
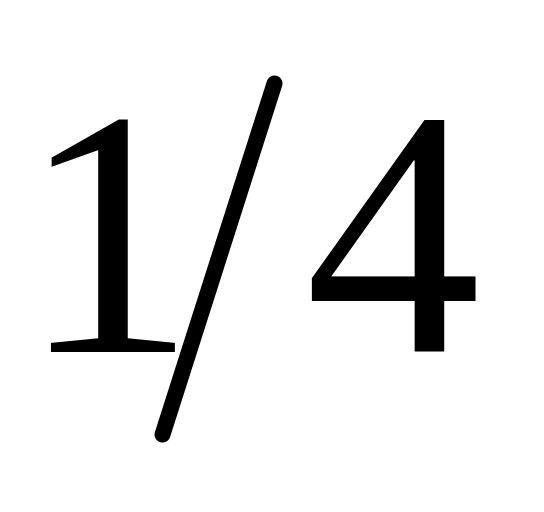
	j	0	–	0	–	–	41,25

Вычислим оценки получившегося плана, например,

.

План оптимальный, так как для нахождения минимума целевой функции все оценки должны быть отрицательны. Однако он не является целочисленным, составим неравенство (3.13) для второй строки расширенной матрицы

,

.

Приведем это неравенство к каноническому виду и составим матрицу новой системы

 ,

.

Число строк увеличилось, необходимо выбрать третью базисную переменную либо х₂, либо х₄, либо х₅. Для каждой из них соотношение (3.8) выполнено в третьей строке. Пусть это будет х₄.

Разделим третью строку на 0,125, затем, умножив ее на –0,125, прибавим ко второй строке и, умножив на 0,5, прибавим к первой строке.

.

План получился целочисленным, составив по расширенной матрице систему уравнений, найдем базисное решение (16; 0; 26; 2; 0; 0). Учитывая, что в исходной системе три неизвестные, оптимальным целочисленным планом будет вектор (16; 0; 26).

W(16; 0; 26) = 16+26 = 42.

Итак, для получения необходимого числа заготовок нужно 42 бревна, 16 из них распилить на 4 части по 1 м и 26 на три части 1,5, 1,5 и 1 м.

Если бы вместо последней базисной переменной выбрали бы не х₄, а х₂ либо х₅, то план получился бы нецелочисленным и необходимо было бы составлять следующее ограничение (2.13) на вновь получившиеся дробные части и т.д., но решение в итоге получилось бы таким же.

40