Глава 2 Линейные методы оптимального управления

§ 2.1. Математические оптимизационные модели.

Общая постановка задачи линейного программирования.

Графический метод решения задачи линейного

Программирования

Математические оптимизационные модели.

Современная экономическая теория включает в себя как необходимый элемент исследования метод математического моделирования.

Математической моделью объекта или явления называется его отображение в виде совокупности разного рода уравнений, неравенств, логических отношений, графиков.

Использование математики позволяет выделить и формально описать наиболее важные, существенные связи экономических переменных и объектов и получить из них новые знания об объекте, используя абстрактные математические методы исследования.

Существуют различные типы моделей.

Оптимизационные модели – модели, преследующие цель выбора наименьшего или наибольшего значения некоторого критерия при условии выполнения системы ограничений. Подобные микромодели могут использоваться в теории управления, для обоснования принятия того или иного решения. В следующих параграфах мы будем изучать оптимизационные математические модели.

Раздел математики, занимающийся методами оптимизации, называется теорией оптимального управления. Она включает в себя такие подразделы как линейное программирование, нелинейное программирование, динамическое программирование и другие.

Основные этапы построения оптимизационной математической модели на примере линейных методов можно представить следующим образом.

1 Этап. Выбор критерия эффективности.

Целью задачи является принятие решения, при котором некоторый параметр примет наибольшее или наименьшее значение. Функция, которая выражает значение этого параметра, является критерием эффективности принятого решения и называется целевой функцией.

Например, критерием эффективности некоторого предприятия может служить прибыль, стремящаяся принять наибольшее значение, или расходы на организацию предприятия, которые должны быть минимальными.

2 Этап. Определение параметров условия.

Параметры условия – постоянные величины, значение которых нельзя изменить в условиях данной задачи.

3 Этап. Выбор параметров управления.

Переменные величины, изменяя значения которых, можно изменить значение критерия эффективности, называют параметрами управлениия. Набор параметров управления называют планом. Всякий набор значений переменных х₁ , х₂ , . . . , х_n удовлетворяющий системе ограничений, называют допустимым планом.

Тот допустимый план, при котором целевая функция принимает максимальное (или минимальное) значение, называют оптимальным планом (стратегией, управлением).

4 Этап. Составление системы ограничений.

Система ограничений  совокупности соотношений (уравнений или неравенств), которые связывают параметры управления и параметры условия.

5 Этап. Выражение целевой функции через параметры условия и параметры управления.

Пример. Составить математическую модель задачи:

Мебельная фабрика для сборки столов и стульев привлекает к работе на 10 дней четырех столяров. Каждый столяр затрачивает на сборку стола 2 часа и 30 минут на сборку стула. Обычно покупатели приобретают вместе со столом от четырех до шести стульев. Доход от одного стола составляет 135 ден. ед. и 50 ден. ед.– от одного стула. Сколько надо произвести за 10 дней стульев и столов, чтобы прибыль от их производства была максимальной. На фабрике установлен 8-часовой рабочий день.

1 этап. Критерием эффективности F является прибыль от производства столов и стульев одним столяром.

2 этап. Представим параметры условия в табличном виде.

	Время	Доход
Столы	2	135
Стулья	0,5	50

3 этап. Параметрами управления являются переменные:

х₁ число производимых столов и х₂ число производимых стульев за 10 дней одним мастером.

4 этап. Ограниченным ресурсом является время. 2х₁ – время, затрачиваемое одним мастером на производство всех столов, 0,5х₂ – время, затрачиваемое одним мастером на производство всех стульев.

Следовательно, 2х₁ +0,5х₂80,

так как время работы мастера ограничено 80 часами за 10 дней.

Кроме этого ограничением является предположение о количестве продаваемых стульев по отношению к продаваемым столам:

4х₁  х₂ 6х₁.

Так же ограничением является неотрицательность переменных х₁ и х₂:

х₁ 0, х₂  0.

Итак, система ограничений имеет вид:

(2.1)

5 этап. Функция прибыли является сумой доходов за все произведенные столы и все произведенные стулья. F выражается через х₁ и х₂ и стремится принять наибольшее значение:

.

Общая постановка задачи линейного программирования

В зависимости от вида целевой функции и системы ограничений выбираются различные методы нахождения оптимального плана.

Рассмотрим математические модели изучаемых процессов, представленных в виде совокупности линейных соотношений.

В этом случае оптимальное решение будет находиться методами линейного программирования.

Термин “линейное программирование” впервые появился в 1951г. в работах американских ученых Дж. Данцига и Т. Кумпанса, а первые работы по линейному программированию были выполнены в конце 30-х годов в Ленинградском государственном университете Л. В. Канторовичем. Употребление слова “программирование” связано с тем, что при решении задач находят такой набор переменных, который является программой (планом) при выполнении поставленной задачи.

Математическая задача линейного программирования в канонической форме формулируется следующим образом:

Найти такие неотрицательные значения х₁ , х₂ , х₃ , . . . , х_n, которые обеспечивают оптимальное (минимальное или максимальное) значение линейной функции (целевой функции)

F= +с

и удовлетворяют системе ограничений

(2.2)

Коэффициенты , с известные постоянные, характеризующие условия задачи (параметры условия).

Система уравнения (2.2) должна быть неопределенной, так как только в этом случае возможен выбор решения из множества возможных.

Задача линейного программирования может не иметь решений в следующих случаях:

1) если система ограничений несовместна, в том числе, если только не выполняется условие неотрицательности переменных x_i;

2) система ограничений совместна, есть допустимые решения, но среди них нет оптимального решения.

От системы ограничений, заданной в виде неравенств, при необходимости всегда можно перейти к канонической системе ограничений, добавив или отняв, дополнительные неотрицательные переменные. Эти переменные имеют вполне определенный экономический смысл. Так, если в ограничениях задачи отражается расход и наличие производственных ресурсов, то дополнительные переменные в оптимальном плане будут характеризовать объем неиспользованных ресурсов.

Пример. Приведите к каноническому виду систему ограничений (2.1) из задачи о производстве столов и стульев.

Введем неотрицательные переменные х₄ , х₅ , х₆.

Перепишем систему неравенств в виде:

Так как левая часть первого неравенства меньше правой, то, добавив к ней положительную переменную х₄, можем вместо неравенства записать уравнение: 2х₁ +0,5х₂+ х₄ = 80. Переменная х₄ играет роль неизрасходованных часов рабочего времени. Аналогично, так как левая часть второго неравенства больше правой, то, отняв он нее положительную переменную х₅, можем вместо неравенства записать уравнение: х₂ – 4х₁– х₅=0. Переменная х₅ показывает, на сколько количество проданных стульев больше учетверенного количества столов и т.д.

Система (2.1) в каноническом виде имеет вид:

Графический метод решения задачи линейного программирования

Если математическая модель задачи линейного программирования имеет два параметра управления, и система ограничений представляет собой систему неравенств, то задача может быть решена графическим методом.

Графический метод основан на геометрической интерпретации области решений системы ограничений и выборе из нее точки, в которой целевая функция принимает оптимальное значение.

Как говорилось ранее, решением системы неравенств с двумя переменными является выпуклая область – пересечение полуплоскостей, представляющих собой решение каждого неравенства. Эту область называют областью допустимых решений (ОДР) или многоугольником решений.

Каждое значение целевой функции F₀ = c₁x₁+c₂x₂ задает на плоскости прямую, называемую опорной. Все эти прямые параллельны между собой и перпендикулярны вектору, называемому градиентом функции и имеющему координаты:

grad F = (c₁; c₂).

Особенностью задачи линейного программирования является то, что с перемещением любой опорной прямой параллельно в одну сторону значение целевой функции либо только растет, либо только убывает. Градиент показывает направление, в котором значение целевой функции будет возрастать. Поэтому, перемещая опорную прямую до «выхода» из ОДР в направлении градиента, будем получать все большие значения целевой функции на каждой из прямых. Наибольшее же будет достигаться в точке «выхода», соответствующей обычно одному из углов многоугольника.

Это рассуждение иллюстрирует теорему линейного программирования:

Оптимальное решение задачи, если оно существует и единственное, достигается в одной из угловых точек многоугольника решений системы ограничений.

Покажем на примере алгоритм решения задачи графическим методом.

Алгоритм решения задачи графическим методом.

Пример. Найдите наибольшее значение функции

F = 2 x₁ + 3 x₂ – 3 при следующих ограничениях

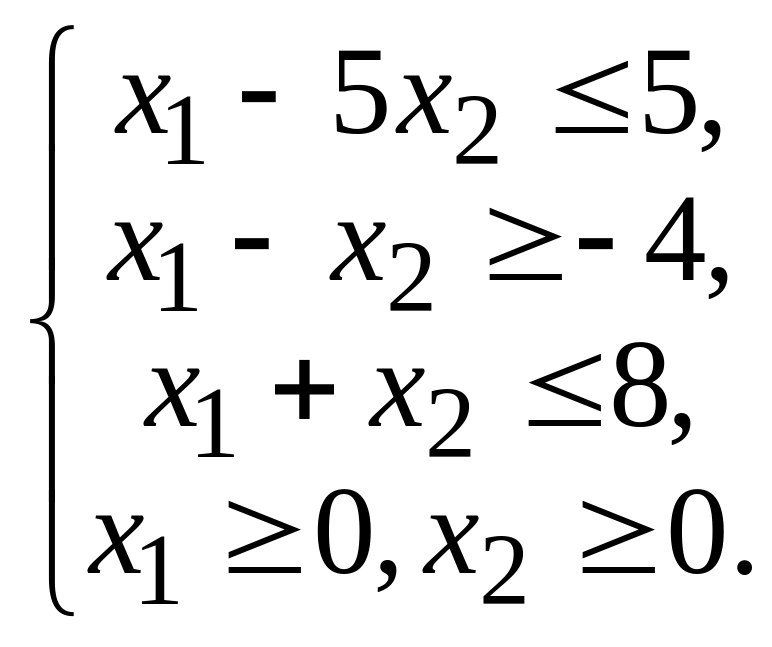(2.3)

1. Найдем область допустимых решений. Для этого построим прямые:

(1)

(2)

(3)

(4)

(5)

отметим штриховкой «допустимые» полуплоскости – решения каждого из неравенств системы (3). Многоугольник ОАВСД (рис.2.1) и есть область допустимых решений (ОДР).

Среди этих решений требуется найти оптимальное, т.е. среди всех точек выпуклого многоугольника ОАВСД, надо найти такую точку, координаты которой обращают в максимум линейную функцию

F = 2 x₁ + 3 x₂ – 3.

2. Построим опорную прямую. Для этого придадим F определенное числовое значение, например, возьмем F = 0, получим линейное уравнение с двумя неизвестными 2 x₁ + 3 x₂ – 3 = 0 , график которого есть прямая линия на плоскости, на рис.2.1 она обозначена L.

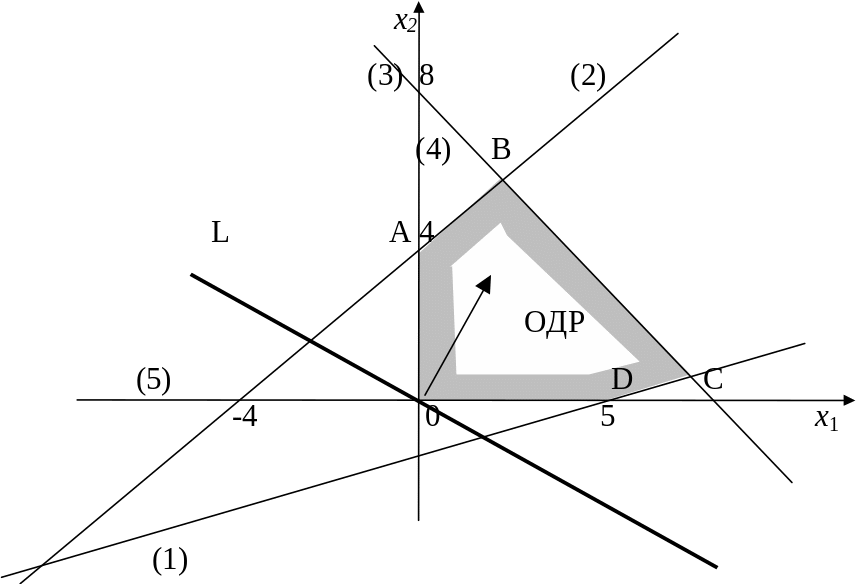
Рис. 2.1

3. Построим вектор градиент функции z:

grad F = (2; 3).

4. Переместим прямую L параллельно самой себе в направлении градиента до выхода из ОДР. Функция F достигнет своего оптимального (максимального) значения в точке В  «точке выхода» из области допустимых решений.

5. Определим координаты точки В. Точка В является точкой пересечения прямых (1) и (3), следовательно, ее координаты находятся из системы уравнений

Решая эту систему, получим: х₁ = 2; х₂ = 6.

Теперь вычислим значение целевой функции z = 2 x₁ + 3 x₂ – 3 при этих значениях неизвестных: z = 2  2 + 3  6 – 3 = 19.

Итак, наибольшее значение функции z = 2 x₁ + 3 x₂ – 3 равно 19, и оно достигается при х₁ = 2; х₂ = 6 .

Если же передвигать опорную прямую в противоположную сторону, то можно найти точку «входа», точку в которой достигается минимальное значение целевой функции. В последнем примере это точка О(0;0).