22

Вопрос №1 Вектор . Линейные операции над веторами.

Вектор – это направленный отрезок, т.е. отрезок с указание точек начала и конца. Вектор обозначается AB или а . Линейные операции над векторами: сложение, вычитание векторов, и умножение вектора на число. По правилу многоугольника(«треугольник» для большего кол-ва чем два вектора):

Начало каждого следующего вектора совмещаю с концом предыдущего. Суммой этих векторов, будет вектор, соединяющий начало первого вектора с концом последнего вектора.

При умножении С и А сонаправлены, если число на которое умножаем больше нуля.

С и А противоположно направлены , если число меньше нуля.

Если С равен нулю, то число равно нулю. Разность векторов – это сумма вектора А и вектора, противоположному вектору В, т.е. А-В=А+(-В).

Вопрос №2 Линейно зависимая и линейно независимая с-ма координат.

Векторы Е₁ Е₂ Е_n называются линейно зависимыми, если существуют числа L₁ L₂ L_n, не равные нулю, такие, что

E₁*L₁+E₂*L₂+….+E_n*L_n

Если это соотношение возможно только при числах равных нулю, то векторы называются линейно зависимыми. Два вектора линейно независимы, тогда и только тогда, когда они неколлинеарны.

Вопрос №3 Проекция вектора на ось.

Проекцией вектора АВ на ось L называется число Пр_LАВ, равно +- |A1В1|, где А1, В1 – проекции точек А, В соответственно; знак «+» берётся, если направление A1В1 совпадает с направлением оси, знак «-» берётся, если эти направления противоположны.

Св-во 1:

Если векторы равны, то равны и их проекции

Св-во 2:

Пр_LА=|А|*cos(a), где а – угол между вектором а и осью L.

Вопрос №4

Базис в пространстве — любые три некомпланарных вектора, взятых в определенном порядке.

Ортонормированный базис – это базис, состоящий из перпендикулярных друг другу векторов, длина которых равна 1.

Прямоугольная декартова система координат на плоскости определяется точкой О(началом координат) и ортонормированным базисом I,j. Прямые, проходящие через начало координат в направление базисных векторов называются координатными осями(соответственно ОХ –ось абцисс, OY – ось ординат).

Любой вектор можно разложить по базису А=[число]*i+[число]*j.

Например, если у вектора А первая координата 2, а вторая 3, то можно записать:

А=2i+3j или А=(2,3).

Вопрос №5

Коллинеарность векторов. Векторы коллинеарны тогда, когда их координаты пропорциональны.

Вопрос №6

Длина вектора- это его модуль, модуль равен корню из суммы квадратов координат.

Направление вектора А удобно задавать с помощью углов альфа, бета, гамма, которые образуют вектор с осями OX,OY,OZ соответственно. Косинусы этих углов называют направляющими косинусами вектора А. По свойству проекций имеем:

Сos(вставить название угла)=соответствующая координата(x,y,z) / модуль самого вектора.

Пусть A и B - две точки координатной плоскости. Их координаты соответственно (x1 ; y1 ) и (x2 ; y2 ). Тогда координаты вектора таковы: (x2 - x1 ; y2 - y1 ). Они получаются вычитанием из координат конца вектора координат его начала .

Понятно, что в какой бы точке плоскости мы ни поместили начало вектора, его координаты будут одними и теми же.

Вопрос №7

Скалярное произведение – это число равное произведению длин этих векторов на косинус угла между ними.

Вектор а*b=|a|*|b|*cos (a,b);

Свойства скалярного произведения.

Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a ^b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а¹ 0 ¹b, то а ^ b.

Вопрос №8 Векторное произведение

Векторное произведение – это вектор, обозначается так [А]x[В] такой, что равен произведению модулей соответствующих векторов(А,В) на синус угла q, где q наименьший из углов между векторами.

Свойства: вектор [А]x[В] перпендикулярен к А и В.

Вектор [А]x[В] направлен так, что кратчайший поворот от А к В виден с его конца как поворот против часовой стрелки, то есть векторы А и В + А x В образуют правую тройку.

Модуль векторного произведения равен площади параллограмма, построенного на этих векторах.

Вопрос № 9

Сме́шанное произведе́ние векторов  — скалярное произведение вектора а на векторное произведение векторов и :

• Смешанное произведение кососимметрично по отношению ко всем своим аргументам:

т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что

• Смешанное произведение в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и :

• Смешанное произведение в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и , взятому со знаком "минус":

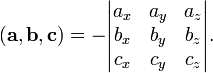р

В частности,

• Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.

• Геометрический смысл — Смешанное произведение по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами и ; знак зависит от того, является ли эта тройка векторов правой или левой.

Вопрос №10 Общее уравнение прямой на плоскости Ах+By+C=0

Если А=0 ,то прямая параллельна оси Ох.

Если В=0 , то пряма парраллельна оси Оу.

С=0 , то прямая проходит через начало координат.

А,В- Координаты нормального вектора(n) и он перпендикулярен.

С является просто координатой.

Расстояние точки A(x1, y1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле

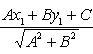
Вопрос№11 Каноническое уравнение прямой на плоскости.

Уравнение прямой, проходящей через две различные точки М0(x0, y0) и М1(x1, y1), имеет вид

Это следует из того, что вектор является направляющим вектором прямой.

Вопрос №12. Уравнение прямой с угловым коэффициентом.

Вопрос №13. Общее уравнение плоскости. Взаимное расположение плоскостей. Расстояние от точки до плоскости.

Плоскостью называеться поверхность все точки которой удовлетворяют общему уравнению. Общее уравнение плоскости: Ax + By + Cz + D = 0

где А, В, С – координаты вектора -вектор нормали к плоскости.

Взаимное расположение плоскостей:

Параллельные плоскости

Получим условия параллельности или совпадения двух плоскостей и заданных общими уравнениями:

( 4.23)

Необходимым и достаточным условием параллельности или совпадения плоскостей (4.23) является условие коллинеарности их нормалей Следовательно, если плоскости (4.23) параллельны или совпадают, то т.е. существует такое число что

и наоборот.

Таким образом, плоскости (4.23) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число что но Плоскости (4.23) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны:

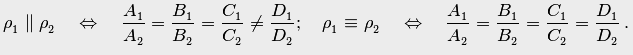
Пересекающиеся плоскости

Необходимым и достаточным условием пересечения двух плоскостей (4.22) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:

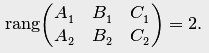
(4.25)

При этом условии система уравнений