
45)Линейная зависимость и линейная независимость векторов. Примеры.
О пределение
С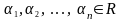 овокупность
векторов называется
линейно
зависимой (ЛЗС),
овокупность
векторов называется
линейно
зависимой (ЛЗС),
е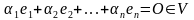 сли
найдутся числа ,
не равные нулю одновременно, такие, что
выполняется равенство:
сли
найдутся числа ,
не равные нулю одновременно, такие, что
выполняется равенство:

В противном случае совокупность называется линейно независимой (ЛНС).
П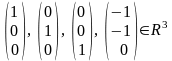 окажем,
что система столбцов
окажем,
что система столбцов
линейно зависима.
Д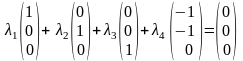 ействительно,
ействительно,
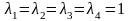
О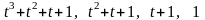 чевидно,
что полученная СЛУ имеет нетривиальные
решения (например,
).
чевидно,
что полученная СЛУ имеет нетривиальные
решения (например,
).
П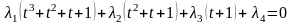 окажем,
что система многочленов
линейно
независима.
окажем,
что система многочленов
линейно
независима.
Д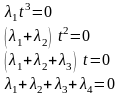 ействительно,
ействительно,
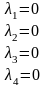
46)Евклидово пространство. Определение и простейшие свойства скалярного пространства.
О пределение.
пределение.
Д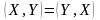 ействительное
линейное пространство E
называется
евклидовым
пространством
,
если каждой паре векторов X
и Y
из E
поставлено
в соответствие действительное число
, называемое скалярным
произведением
векторов X
и Y,
причем выполнены следующие условия:
ействительное
линейное пространство E
называется
евклидовым
пространством
,
если каждой паре векторов X
и Y
из E
поставлено
в соответствие действительное число
, называемое скалярным
произведением
векторов X
и Y,
причем выполнены следующие условия:
1 )
;
)
;
2 )
;
)
;
3)
47)Длина вектора. Угол между векторами. Ортогональность векторов.
О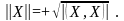 пределение.
пределение.
Д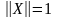 линой
вектора
X
называется число
линой
вектора
X
называется число
Если , то вектор X называется нормированным.
А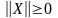 лгебраические
свойства длины вектора:
лгебраические
свойства длины вектора:
1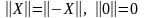 )
;
)
;
2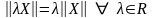 )
;
)
;
3) .
Угол между векторами.
Углом
между векторами
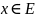 и
и
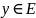 называют угол
называют угол
 ,для
которого
,для
которого
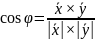 ,
,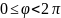
Ортогональные векторы.
Векторы
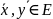 ортогональны, если
ортогональны, если
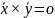
4 8)Скалярное
произведение в Rn.
Длина вектора и угол между векторами в
Rn.
8)Скалярное
произведение в Rn.
Длина вектора и угол между векторами в
Rn.
Определение.
Скалярным произведением векторов
н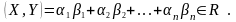 азывается
число
азывается
число
С войства скалярного произведения выполнены:
1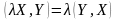 )
;
)
;
2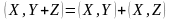 )
;
)
;
3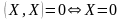
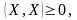 )
;
)
;
4) причем
Д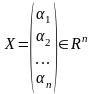 лина
вектора.
лина
вектора.
Определение.
Длиной вектора называется число
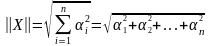
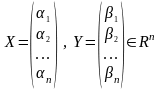
Угол между векторами.
Угол между ненулевыми векторами
в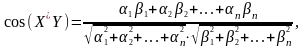 пространстве Rn
:
пространстве Rn
:
У словие
ортогональности векторов:
словие
ортогональности векторов:
49)Неравенство Коши-Буняковского.
Д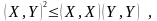 ля
любых векторов X
и Y
евклидова пространства E
справедливо
неравенство
Коши-Буняковского
ля
любых векторов X
и Y
евклидова пространства E
справедливо
неравенство
Коши-Буняковского
к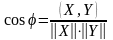 оторое
позволяет следующим образом определить
угол между ненулевыми векторами:
оторое
позволяет следующим образом определить
угол между ненулевыми векторами:
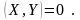
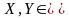
Ненулевые векторы E называются ортогональными, если
50)Построение ортогональго базиса в Rn.
Задача.
П роверить
ортогональность системы векторов
роверить
ортогональность системы векторов
и дополнить ее до ортогонального базиса.
Р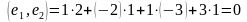
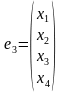 ешение.
ешение.
Д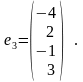 ля
определения достаточно
найти какое-либо
ля
определения достаточно
найти какое-либо
р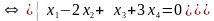
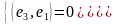 ешение
системы
ешение
системы
Д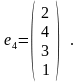
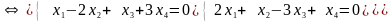
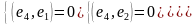 ля
определения e4
ля
определения e4
51) Ортонормированный базис.
О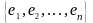 пределение.
пределение.
Б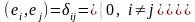 азис
n-мерного
евклидова пространства называется
ортонормированным,
если
азис
n-мерного
евклидова пространства называется
ортонормированным,
если
Другими словами, ортонормированным базисом называется базис, состоящий из попарно ортогональных векторов, каждый из которых имеет длину, равную единице
52)Процесс ортогонализации Шмидта.
Теорема (об ортогонализации)
В любом подпространстве евклидова пространства E
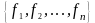 можно
выбрать ортонормированный базис.
можно
выбрать ортонормированный базис.
Е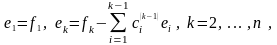 сли
задан произвольный базис
, то векторы
сли
задан произвольный базис
, то векторы

где , образуют ортогональный базис,
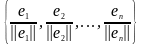
а - ортонормированный базис.
53)Ортогональное дополнение подпространства Rn. Определение и свойства.
Определение
О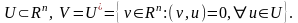 ртогональным
дополнением
подпространства
U
из
Rn
называется подпространство, состоящее
из векторов, ортогональных любому
вектору из U.
ртогональным
дополнением
подпространства
U
из
Rn
называется подпространство, состоящее
из векторов, ортогональных любому
вектору из U.
С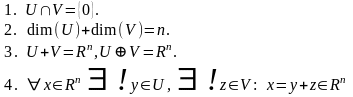 войства
ортогонального дополнения:
войства
ортогонального дополнения:
5 4)Расстояние
и угол между вектором и подпространством.
4)Расстояние
и угол между вектором и подпространством.
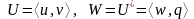
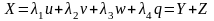
Ортогональная составляющая
Проекция
Д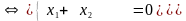
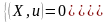 ля
нахождения w
и q
достаточно найти какие-либо два решения
системы
ля
нахождения w
и q
достаточно найти какие-либо два решения
системы
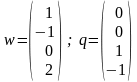
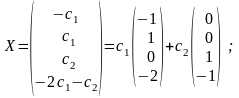

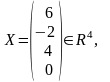
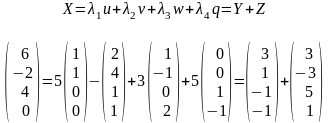
Z
Y
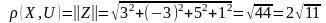
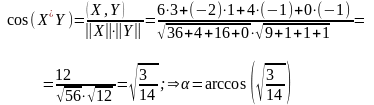
5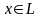 5)
Определение линейного оператора. Пример.
5)
Определение линейного оператора. Пример.
Л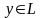 инейным
оператором в линейном пространстве
L
называется всякое отображение A
: L
→ L
пространства
в себя, ставящее каждому
инейным
оператором в линейном пространстве
L
называется всякое отображение A
: L
→ L
пространства
в себя, ставящее каждому
е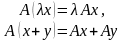 динственный
элемент , и обладающее
динственный
элемент , и обладающее
свойствами
Пример 1.
Я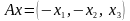 вляется
ли отображение A:
R3→
R3
вляется
ли отображение A:
R3→
R3
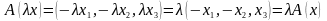 —
поворот
пространства R3
на
угол p
относительно вектора k=(0,0,1)
— линейным оператором?
—
поворот
пространства R3
на
угол p
относительно вектора k=(0,0,1)
— линейным оператором?
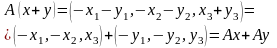
Отображение A является линейным оператором.
Пример 2.
Я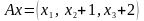 вляется
ли отображение A
: R3→
R3
вляется
ли отображение A
: R3→
R3
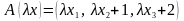 л
инейным
оператором?
л
инейным
оператором?
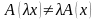
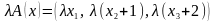
Отображение A не является линейным оператором.
5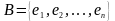 6)Матрица
линейного оператора. Определение и
пример.Пусть A
– линейный оператор в конечномерном
6)Матрица
линейного оператора. Определение и
пример.Пусть A
– линейный оператор в конечномерном
пространстве Ln и – некоторый фиксированный базис.
Р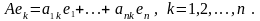 азложим
векторы Aek
по базису B:
азложим
векторы Aek
по базису B:
Т огда матрица
называется матрицей оператора A в базисе B.
Пример 3.
Оператор A: R3→ R3 поворота пространства R3
на угол p относительно вектора k=(0,0,1)
является линейным оператором.
Е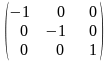
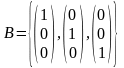 го
матрица в ортонормированном базисе
го
матрица в ортонормированном базисе
имеет вид
Пример 4.
Л инейные
операторы A и B действуют
в R3
инейные
операторы A и B действуют
в R3
следующим образом:
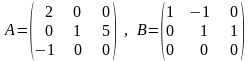 для
всех x из
R3
для
всех x из
R3
57)Ядро и образ линейного оператора. Определение и пример.
Ядром линейного оператора называется множество элементов из L , образом которых является нулевой элемент.
Я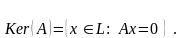 дро
оператора обозначают Ker(A) :
дро
оператора обозначают Ker(A) :
Ядро линейного оператора - линейное пространство.
Рассмотрим линейный оператор A , действующий в конечномерном линейном пространстве L .
О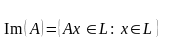 бразом
линейного оператора
называется
бразом
линейного оператора
называется
П ример(о.п.):
ример(о.п.):
П роверить, принадлежат ли векторы u и v образу оператора.
Е
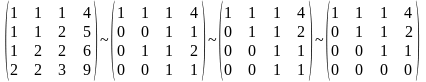 сли
базисные столбцы матрицы оператора и
рассматриваемый вектор образуют
линейно зависимую систему, то вектор
принадлежит Im(A). В противном случае
вектор не прина-длежит Im(A) .
сли
базисные столбцы матрицы оператора и
рассматриваемый вектор образуют
линейно зависимую систему, то вектор
принадлежит Im(A). В противном случае
вектор не прина-длежит Im(A) .
1.
В
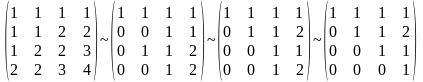 ектор
u принадлежит Im(A) .
ектор
u принадлежит Im(A) .
2.
Вектор v не принадлежит Im(A) .
П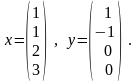 ример(я.о):
ример(я.о):
П
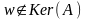
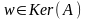 роверить,
принадлежат ли векторы x и y
ядру оператора A.
роверить,
принадлежат ли векторы x и y
ядру оператора A.
Е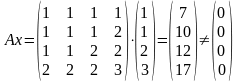 сли
для рассматриваемого вектора w
Aw=O
,то . В противном случае
сли
для рассматриваемого вектора w
Aw=O
,то . В противном случае
1.
В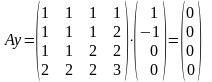 ектор
x
не принадлежит Ker(A)
.
ектор
x
не принадлежит Ker(A)
.
2.
Вектор y принадлежит Ker(A) .
58)Преобразование матрицы линейного оператора при преобразовании базиса.
О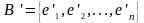
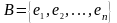 пределение.
пределение.
М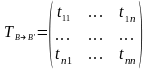 атрицей
перехода от базиса
к базису
называется
матрица
атрицей
перехода от базиса
к базису
называется
матрица
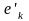 ,
,
k-й столбец которой есть столбец координат вектора в базисе B.
59)Приведение матрицы оператора к диагональному виду.
Пусть A и A’ – матрицы оператора A в базисахB и B’, а T = TB→B’ – матрица перехода от базисаB к базису B’.
Т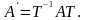 огда
формула преобразования матрицы
оператора при преобразовании базиса
имеет вид
огда
формула преобразования матрицы
оператора при преобразовании базиса
имеет вид
Если оператор A, действующий в пространстве Ln , имеет n линейно независимых собственных векторов e1, e2, … , en , соответствующих собственным числам
λ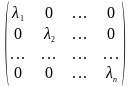 1,
λ2,
… , λn
,
то в базисе из этих векторов матрица
оператора A
имеет диагональный вид
1,
λ2,
… , λn
,
то в базисе из этих векторов матрица
оператора A
имеет диагональный вид
60)Квадратичная формула. Определение и пример.
К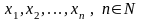 вадратичной
формой
называется однородный многочлен второй
степени от нескольких переменных над
полем вещественных чисел.
вадратичной
формой
называется однородный многочлен второй
степени от нескольких переменных над
полем вещественных чисел.
П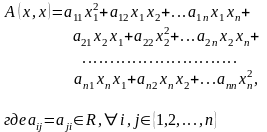 усть
- переменные.
Тогда
усть
- переменные.
Тогда
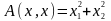
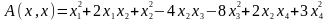 - квадратичная
форма в R2.
- квадратичная
форма в R2.
- квадратичная форма в R4.
61)Матрица квадратичной формы. Определение и пример.
М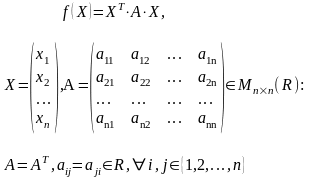 атричной
записью квадратичной формы
называется следующее выражение:
атричной
записью квадратичной формы
называется следующее выражение:
6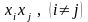 2)Канонический
и нормальный вид квадратичной формы.
Определение и пример.
2)Канонический
и нормальный вид квадратичной формы.
Определение и пример.
П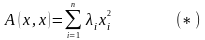 усть
в некотором базисе выражение квадратичной
формы не содержит произведений
, т.е.
усть
в некотором базисе выражение квадратичной
формы не содержит произведений
, т.е.
Т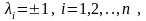 огда
выражение (*) называется каноническим
видом
квадратичной формы.
огда
выражение (*) называется каноническим
видом
квадратичной формы.
В частности, если
то получаем нормальный вид квадратичной формы.
63) Методы приведения квадратичной формы к каноническому виду. Идея метода Лагранжа. Пример.
Любую вещественную квадратичную форму невырожденным линейным преобразованием переменных можно привести к диагональному виду, т.е. преобразованная квадратичная форма состоит только из квадратов новых переменных с некоторыми коэффициентами.
Пример:
К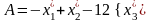 вадратичная
форма принимает канонический(диагональный)
вид
вадратичная
форма принимает канонический(диагональный)
вид
П ри
этом
ри
этом
64) Методы приведения квадратичной формы к каноническому виду. Идея метода собственных векторов. Пример.
65) Теоремы об ортогональном преобразовании вещественных квадратичных форм.
Л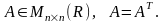
 юбую
вещественную квадратичную форму можно
привести к диагональному виду при помощи
линейного преобразования переменных
с ортогональной матрицей.
юбую
вещественную квадратичную форму можно
привести к диагональному виду при помощи
линейного преобразования переменных
с ортогональной матрицей.
П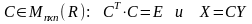 усть
, где
усть
, где
Т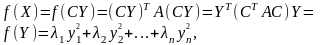 огда
существует
огда
существует
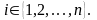
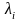
где – собственные числа матрицы А, а столбцы матрицы С – собственные векторы,
