
- •16)Характеристическое уравнение матрицы
- •18) Норма — структура длины векторов на линейном пространстве.
- •Для всех (неравенство треугольника);
- •19) Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы.
- •20)Евклидово пространство
6 ) Свойства и признаки
Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны
Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну
Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны
Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях
7) Две плоскости пересекаются по прямой линии. Для построения линии их пересечения необходимо найти две точки, принадлежащие этой линии. Задача упрощается, если одна из пересекающихся плоскостей занимает частное положение. В этом случае ее вырожденная проекция включает в себя проекцию линии пересечения плоскостей.
8) Пусть плоскости и заданы соответственно уравнениями и . Требуется найти угол между этими плоскостями. Плоскости, пересекаясь, образуют четыре двугранных угла (рис. 11.6): два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой.
Двугранный угол, линейный угол двугранного угла, угол между двумя пересекающимися плоскостями. Для нахождения угла между пересекающимися плоскостями α и β выбирают какую-нибудь точку С, принадлежащую линии с их пересечения, и восстанавливают перпендикуляры a и b к линии c, лежащие в плоскостях α и β соответственно. Угол между прямыми a и b будет искомым углом между плоскостями α и β.
Если линия пересечения плоскостей α и β, указанных в задаче, не дана или находится вне данного рисунка, то для нахождения угла между плоскостями α и β выбирают какие-нибудь плоскости α’ и β’ соответственно параллельные α и β, линия пересечения которых расположена на рисунке. При этом одна из плоскостей α’ и β’ может совпадать соответственно с α или β. После этого находят угол между плоскостями α’ и β’.
9)§ 1. Каноническое уравнение плоскости в пространстве
Пусть в декартовой системе координат дан вектор n={A,B,C} и точка М0=(x0,y0,z0).
Построим плоскость Π, проходящую через т. М0, перпендикулярную вектору n (этот вектор называют нормальным вектором или нормалью плоскости).
Каноническое уравнение плоскости в пространстве:
Аx+By+Cz+D=0, где D = -Ax0-By0-Cz0.
16)Условия параллельности двух прямых:
а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
k1 = k2.
б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
А/А1= B/B1
18) Две прямые в трёхмерном евклидовом пространстве скрещиваются, если не существует плоскости, их содержащей. Иначе говоря, две прямые в пространстве, не имеющие общих точек, но не являющиеся параллельными.
1) Линейное, или векторное пространство над полем P — это непустое множество L, на котором введены операции
1.сложения, то есть каждой паре элементов множества ставится в соответствие элемент того же множества, обозначаемый и
2.умножения на скаляр (то есть элемент поля P), то есть любому элементу и любому элементу ставится в соответствие единственный элемент из , обозначаемый .
При этом на операции накладываются следующие условия:
1., для любых (коммутативность сложения);
2., для любых (ассоциативность сложения);
3.существует такой элемент , что для любого (существование нейтрального элемента относительно сложения), в частности L не пусто;
4.для любого существует такой элемент , что (существование противоположного элемента относительно сложения).
5. (ассоциативность умножения на скаляр);
6. (унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).
7. (дистрибутивность умножения на вектор относительно сложения скаляров);
8.(дистрибутивность умножения на скаляр относительно сложения векторов).
Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомамиабелевойгруппы.
2) В математике слово «пространство» употребляется в большом наборе сложных терминов. Примеры:
Аффинное пространство
Банахово пространство
Вероятностное пространство
Гильбертово пространство
Евклидово пространство
Нормированное пространство
Векторное пространство
Метрическое пространство
Топологическоепространство
Пространство с мерой
ПространствоLp
3) ЛИНЕЙНАЯ ОБОЛОЧКА ВЕКТОРОВ [linearhull] — множество линейных комбинаций этих векторов ∑αiai со всеми возможными коэффициентами (α1, ..., αn).
4) В линейной алгебре линейная зависимость — это свойство, которое может иметь подмножество линейного пространства. Для этого должна существовать нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу. Если такой комбинации нет, то есть коэффициенты единственной такой линейной комбинации равны нулю, множество называется линейно независимым.
5) Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов.
8)Преобразование координат при переходе к новому базису
1)
Дано:
![]()
Записать
вектор
![]() в
базисе векторов
в
базисе векторов
![]() .
Решение:
Чтобы
векторы образовывали базис нужно, чтобы
они были некомпланарны, т.е. их векторное
произведение (объем параллелепипеда
на векторах) не равнялось нулю.
.
Решение:
Чтобы
векторы образовывали базис нужно, чтобы
они были некомпланарны, т.е. их векторное
произведение (объем параллелепипеда
на векторах) не равнялось нулю.
 Вектор
в старом базисе:
Вектор
в старом базисе:
![]() В
новом:
В
новом:
![]() Старые
координаты связаны с новыми
Старые
координаты связаны с новыми
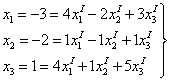 Решив
эту систему с помощью обратной матрицы,
найду координаты вектора
в
новом базисе
Решив
эту систему с помощью обратной матрицы,
найду координаты вектора
в
новом базисе
![]() Матрица,
связывающая старые и новые координаты:
Матрица,
связывающая старые и новые координаты:
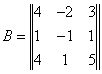 Новые
и старые координаты связаны
отношением:
b=BbI
b
– матрица старых координат;
B –
матрица, связывающая координаты старые
и новые;
BI
– матрица новых координат.
Отсюда:
bI=B-1b
Найду
обратную матрицу B-1.
Новые
и старые координаты связаны
отношением:
b=BbI
b
– матрица старых координат;
B –
матрица, связывающая координаты старые
и новые;
BI
– матрица новых координат.
Отсюда:
bI=B-1b
Найду
обратную матрицу B-1.
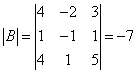 Определитель
≠0 , значит обратная матрица существует.
Найду
алгебраические дополнения:
Определитель
≠0 , значит обратная матрица существует.
Найду
алгебраические дополнения:
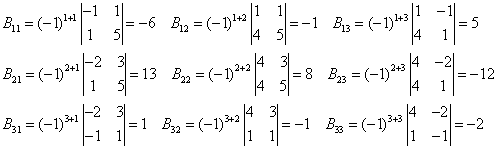
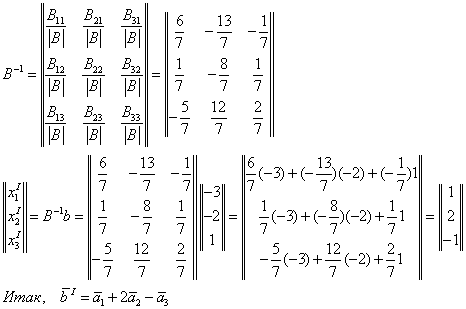
9)Определение
1.Суммой1)
подпространств
![]() и
и
![]() называется
наименьшее подпространство в
называется
наименьшее подпространство в
![]() ,
содержащее
и
,
то есть
,
содержащее
и
,
то есть
![]() .
.
Вообще говоря, можно определить сумму любого конечного числа подпространств:
Определение
1'.
Сумма подпространств
![]() в
—
это наименьшее подпространство,
содержащее все
в
—
это наименьшее подпространство,
содержащее все
![]() ,
то есть
,
то есть
![]() .
.
10)Пусть
и
—
подпространствавекторного
пространства
над
полем![]() .
.
Предложение
1.Пересечение![]() подпространств
и
является
векторным пространством.
подпространств
и
является
векторным пространством.
Замечание
1.Объединение![]() пространств
и
не
обязано быть векторным пространством,
как показано в следующем примере.
пространств
и
не
обязано быть векторным пространством,
как показано в следующем примере.
Пример
1.
Пусть
![]() ,
то есть множество векторов вида
,
то есть множество векторов вида
![]() ,
где
,
где
![]() .
Базисом
этого пространства служат вектора
.
Базисом
этого пространства служат вектора
![]() и
и
![]() .
Положим
.
Положим
![]() и
и
![]() —
линейные
оболочки
векторов
—
линейные
оболочки
векторов
![]() и
и
![]() ,
соответственно. Сумма векторов
,
соответственно. Сумма векторов
![]() не
содержится в
не
содержится в![]() .
.
Определение 1.Суммой1) подпространств и называется наименьшее подпространство в , содержащее и , то есть
.
Вообще говоря, можно определить сумму любого конечного числа подпространств:
Определение 1'. Сумма подпространств в — это наименьшее подпространство, содержащее все , то есть
.
Предложение 2. Пусть и — подпространства конечномерного векторного пространства . Тогда
![]() .
.
Внутренняя прямая сумма
Определение
2.
Пространство
называется
прямой
суммой2)
своих векторных подпространств
,
если каждый вектор
![]() может
быть представлен одним и только одним
способом в виде суммы
может
быть представлен одним и только одним
способом в виде суммы
![]() где
где
![]() .
.
Прямая
сумма векторных пространств обозначается
через![]() .
.
Замечание 2. Определенная таким образом прямая сумма называется внутренней.
Пример
2.
Пусть
и
подпространства
![]() и
и
![]() определены
также, как в примере 1. Тогда сумма
определены
также, как в примере 1. Тогда сумма
![]() является
прямой, то есть
является
прямой, то есть
![]() .
.
Предложение
3.
Сумма
![]() является
прямой тогда и только тогда, когда
выполнено любое из следующих двух
условий:
является
прямой тогда и только тогда, когда
выполнено любое из следующих двух
условий:
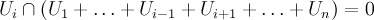 для
для
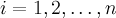 ,
, .
.
Следствие
1.
Если
![]() ,
то сумма
,
то сумма
![]() является
прямой тогда и только тогда, когда
является
прямой тогда и только тогда, когда
![]() .
.
Предложение
4.
Для любого
![]() -мерного
подпространства
векторного
пространства
размерности
-мерного
подпространства
векторного
пространства
размерности
![]() найдется
такое
найдется
такое
![]() -мерное
подпространство
,
что
-мерное
подпространство
,
что
![]() .
.
Внешняя прямая сумма
Пусть и — векторные пространства над полем .
Определение
3.Прямой
суммой
векторных пространств
и
называется
декартово
произведение![]() с
операциями сложения
векторов и умножения
их на скаляр,
определенными следующей формулой:
с
операциями сложения
векторов и умножения
их на скаляр,
определенными следующей формулой:
![]() .
.
Замечание 3. Определенная таким образом прямая сумма называется внешней. Непосредственной проверкой можно убедиться, что внешняя прямая сумма векторных пространств является векторным пространством.
Предложение
5.
Внешняя прямая сумма
![]() пространств
и
обладает
следующим свойством: если
пространств
и
обладает
следующим свойством: если
![]() и
и
![]() —
линейные отображения, определенные
условиями
—
линейные отображения, определенные
условиями
![]() ,
,
![]() ,
то
является
внутренней прямой суммой подпространств
,
то
является
внутренней прямой суммой подпространств
![]() и
и
![]() .
Таким образом,
.
Таким образом,
![]() .
.
12)Определение линейного оператора.Примеры
Определение1.
Пусть
ExиEy 1–линейные пространства над полем
комплексных(или действительных)чисел.
Отображение А: Ex®Eyназываетсялинейнымоператором,если
для любых элементов х1и х2пространстваExи
любого комплексного(действительного)числа
![]() выполняются
следующие равенства 2:
выполняются
следующие равенства 2:
А(х1+х2) = Ах1 + Ах2;
А( х) = А(х);
Примеры линейных операторов:
1) Пусть Е = Е1– линейное топологическое пространство.Оператор А задан формулой:
Ax
= xдля всех x![]() Е.
Е.
Такой оператор,переводящий каждый элемент пространства в себя является линейным и называется единичным оператором.
2) РассмотримD[a,b]– пространство дифференцируемых функций, оператор дифференцирования Д в пространствеD[a,b]задан формулой:
Дf(x) = f/(x).
Где f(x) D[a, b], f/(x) C[a, b].
Оператор Д определен не на всем пространствеC[a, b], а лишь на множестве функций имеющих непрерывную производную.Еголинейность,очевидно, следует из свойств производной.
3)
Рассмотрим пространство С[-![]() ,
+
]–
пространство непрерывных и ограниченных
функций, оператор А сдвигает функцию
наconst a:
,
+
]–
пространство непрерывных и ограниченных
функций, оператор А сдвигает функцию
наconst a:
Аf(x) = f(x+a).
Проверим линейность оператора А:
1) А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g).
Исходя из определения суммы функции,аксиомааддитивности выполняется.
2) A(kf(x)) = kf(x+a) = kA(f(x)).
Верна аксиома однородности.
Можно сделать вывод, что А –линейный оператор.
4)Пусть
![]()
![]()
![]() (пространство
непрерывных функций на отрезке [0,1], и
дано отображение
(пространство
непрерывных функций на отрезке [0,1], и
дано отображение![]() 1,заданное
формулой:
1,заданное
формулой:
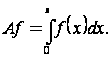
Так
как интеграл с переменным верхним
пределом от непрерывной функции является
функцией дифференцируемой,а,
следовательно,непрерывной,то![]() .В
силу линейности определенного интеграла
данное отображение является линейным
оператором
.В
силу линейности определенного интеграла
данное отображение является линейным
оператором
13)Связь между матрицами одного и того же линейного оператора в разных базисах
Если
в базисе
![]() линейный
оператор
линейный
оператор
![]() имеет
матрицу A,
в базисе
имеет
матрицу A,
в базисе
![]() -
матрицу B,
а S
- матрица перехода от первого базиса ко
второму, то
-
матрицу B,
а S
- матрица перехода от первого базиса ко
второму, то
![]()
14)Преобразование матрицы линейного оператора при переходе к новому базису
Пусть линейный оператор
^ |
A |
: Xn → Xn в базисе e имеет матрицу Ae . Найдем матрицу этого оператора Af в базисе f . Пусть C — матрица перехода от базиса e к базису f .
Теорема.Преобразование матрицы оператора
^ |
A |
при переходе от "старого" базиса e к "новому" базису f определяется формулой:
|
|
(1) |
Доказательство.
Рассмотрим произвольный вектор x и его образ y =
^ |
A |
x . Обозначим координатные столбцы этих векторов: Xe и Ye — в "старом" базисе e ;Xf и Yf — в "новом" базисе f .
Тогда
|
|
|
и
|
|
|
Отсюда, используя формулы преобразования вектора, получаем
|
|
|
Сравнивая с выражением Yf = Af · Xf , приходим к формуле (1), которую требовалось доказать.
15)Собственные числа и собственные векторы линейного оператора
Наиболее
просто устроены матрицы диагонального
вида
 .
Возникает вопрос, нельзя ли найти базис,
в котором матрица линейного оператора
имела бы диагональный вид. Такой базис
существует.
.
Возникает вопрос, нельзя ли найти базис,
в котором матрица линейного оператора
имела бы диагональный вид. Такой базис
существует.
Пусть дано линейное пространство Rn и действующий в нем линейный оператор A; в этом случае оператор A переводит Rn в себя, то есть A:Rn → Rn.
Определение.
Ненулевой вектор
![]() называется
собственным вектором оператора A, если
оператор A переводит
в
коллинеарный ему вектор, то есть
называется
собственным вектором оператора A, если
оператор A переводит
в
коллинеарный ему вектор, то есть
![]() .
Число λ называется собственным значением
или собственным числом оператора A,
соответствующим собственному вектору
.
.
Число λ называется собственным значением
или собственным числом оператора A,
соответствующим собственному вектору
.
Отметим некоторые свойства собственных чисел и собственных векторов.
16)Характеристическое уравнение матрицы
Характеристическим уравнением матрицы
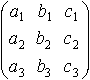
называется уравнение
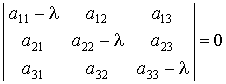
Корни этого уравнения l1, l2, l3 называются характеристическими числами матрицы; они всегда вещественны, если исходная матрица была симметрической. Система уравнений
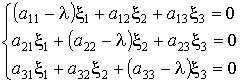
в которой l имеет одно из значений l1, l2, l3 и определитель которой в силу этого равен нулю, определяет тройку чисел (x1, x2, x3), соответствующую данному характеристическому числу. Эта совокупность трех чисел (x1, x2, x3) определяет вектор r=x1i+x2j+x3k, называемый собственным вектором матрицы.
17) Евкли́довопростра́нство (также Эвкли́довопростра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомамиевклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.
В
современном понимании, в более общем
смысле, может обозначать один из сходных
и тесно связанных объектов, определённых
ниже. Обычно n-мерное
евклидово пространство обозначается
![]() ,
хотя часто используется не вполне
приемлемое обозначение
,
хотя часто используется не вполне
приемлемое обозначение
![]()
Примеры
Наглядными примерами евклидовых пространств могут служить пространства:
 размерности
1 (вещественная
прямая)
размерности
1 (вещественная
прямая)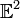 размерности
2 (евклидова
плоскость)
размерности
2 (евклидова
плоскость)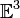 размерности
3 (евклидово
трехмерное пространство)
размерности
3 (евклидово
трехмерное пространство)Евклидово пространство можно считать современной интерпретацией и обобщением (так как оно допускает размерности больше трех) классической (Евклидовой) геометрии.
Более абстрактный пример:
пространство вещественных многочленовp(x) степени, не превосходящей n, со скалярным произведением, определенным как интеграл произведения по конечному отрезку (или по всей прямой, но с быстро спадающей весовой функцией, например
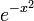 )
)
18) Норма — структура длины векторов на линейном пространстве.
Норма
в векторномлинейном
пространстве![]() над
полемвещественных
или комплексных
чисел
есть функция
над
полемвещественных
или комплексных
чисел
есть функция![]() ,
удовлетворяющая следующим условиям
(аксиомы нормы):
,
удовлетворяющая следующим условиям
(аксиомы нормы):
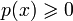 ,
причём p(x)
= 0 только при
,
причём p(x)
= 0 только при
 ;
;Для всех (неравенство треугольника);
p(αx) = | α | p(x) для любого скаляра α.
Норма
![]() обычно
обозначается
обычно
обозначается
![]() .
Линейное пространство с нормой называется
нормированным
пространством,
а условия (1-3) — также аксиомами
нормированного пространства.
.
Линейное пространство с нормой называется
нормированным
пространством,
а условия (1-3) — также аксиомами
нормированного пространства.
Ортогона́льность — понятие, являющееся обобщением перпендикулярности для линейных пространств с введённым скалярным произведением.
Если скалярное произведение двух элементов пространства равно нулю, то они называются ортогональными друг другу.
Важной особенностью понятия является его привязка к конкретному используемому скалярному произведению: при смене произведения ортогональные элементы могут стать неортогональными, и наоборот.
Термин используется в других сложных терминах.
19) Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы.
Неравенство Коши — Буняковского иногда, особенно в иностранной литературе, называют неравенством Шварца и неравенством Коши — Буняковского — Шварца («неравенство КБШ»), хотя работы Шварца на эту тему появились только спустя 25 лет после работ Буняковского[1]. Конечномерный случай этого неравенства называется неравенством Коши и был доказан Коши в 1821 году.
Формулировка
Пусть
дано линейное пространство L
со скалярным произведением
![]() .
Пусть
—
норма, порождённая скалярным произведением,
то есть
.
Пусть
—
норма, порождённая скалярным произведением,
то есть
![]() .
Тогда для любых
.
Тогда для любых
![]() имеем:
имеем:
![]()
причём равенство достигается тогда и только тогда, когда векторы x и y пропорциональны (коллинеарны).
