
- •Понятие марковского случайного процесса. Марковское свойство.
- •Процесс случайного блуждания.
- •Понятие выборки. Вариационный ряд. Гистограмма, полигон частот.
- •Построение доверительного интервала.
- •Свойства оценок неизвестных параметров. Классификация оценок. Оценка методом моментов.
- •Классификация состояний цепей маркова. Уравнение колмогорова.
Понятие выборки. Вариационный ряд. Гистограмма, полигон частот.
Выборка
– совокупность значений, принимаемых
с.в. при измерении. Пусть при измерении
с.в.
имеет значения
 .
Объем такой выборки равен
.
Объем такой выборки равен
 .
.
Имея значения выборки строим вариационный ряд – размещение выборочных значений по возрастанию или убыванию.
Размах
выборки определяется из вариационного
ряда, как
 .
.
Для
определения частот выполняется
группировка. Если имеется выборка
объемом
,
то количество интервалов для значений
с.в. находится из формулы Стерджеса как
 .
.
Зная
размах выборки и количество интервалов
можно найти ширину каждого интервала
как
 .
Частота
.
Частота
 равна количеству значений, попавших на
интервал ширины
равна количеству значений, попавших на
интервал ширины
 .
.

Здесь
 —
— называется полигоном
частот,
а ломаная пунктирная – гистограммой.
С уменьшением интервалов ломаная
превращается в гладкую (аналогично
плотности распределения).
называется полигоном
частот,
а ломаная пунктирная – гистограммой.
С уменьшением интервалов ломаная
превращается в гладкую (аналогично
плотности распределения).
ГИСТОГРАММА И ПОЛИГОН ЧАСТОТ.
Для определения частот выполняется группировка. Если имеется выборка объемом , то количество интервалов для значений с.в. находится из формулы Стерджеса как .
З ная
количество интервалов можно найти
ширину каждого интервала как
,
где
размах выборки. Частота
равна количеству значений, попавших на
интервал ширины
.
ная
количество интервалов можно найти
ширину каждого интервала как
,
где
размах выборки. Частота
равна количеству значений, попавших на
интервал ширины
.
Здесь — называется полигоном частот, а ломаная пунктирная – гистограммой. С уменьшением интервалов ломаная превращается в гладкую (аналогично плотности распределения).
ПУАССОНОВСКИЙ ПРОЦЕСС.
Постулаты:
1)
Вероятность того, что в интервале времени
произойдет изменение состояния равна
 ,
где
,
где
 – интенсивность процесса.
– интенсивность процесса.
2)
Вероятность того, что в интервале времени
не произойдет изменения состояния равна
 .
.
3)
Вероятность
того, что в интервале времени
произойдет более одного изменения
состояния равна
 .
.
Предположим,
что произошло
изменений в момент времени
 ,
тогда
,
тогда

Отсюда
 Разделив обе части на
Разделив обе части на
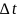 есть
есть
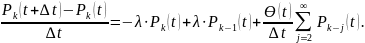 Учитывая, что
Учитывая, что
 и
и
 запишем систему дифференциальных
уравнений Колмогорова
запишем систему дифференциальных
уравнений Колмогорова
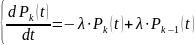 ,
где
При
решении системы все
,
где
При
решении системы все
 выражаются через
выражаются через
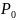 , а
находится из условия нормировки.
, а
находится из условия нормировки.
СИСТЕМА M|Er|1.
 – поток
Эрланга с числом степеней свободы
– поток
Эрланга с числом степеней свободы
 .
Каждая поступившая заявка получает
обслуживание на
этапах. Из-за этого рассматриваемый
процесс в СМО не будет марковским, а
значит, не может решаться через систему
ДУ Колмогорова.
.
Каждая поступившая заявка получает
обслуживание на
этапах. Из-за этого рассматриваемый
процесс в СМО не будет марковским, а
значит, не может решаться через систему
ДУ Колмогорова.
Пусть
имеется СО с
последовательными этапами. Время
обслуживание на одном этапе имеет
экспоненциальное распределение с
параметром
 .
.

Вероятность
того, что
 это
это
 .
.


 –
свертка
функции.
–
свертка
функции.

А налогично
находим
налогично
находим

Пусть
в систему поступило
заявок и принесло
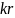 работы. Если обслуживаемая заявка
находится на -том этапе обслуживания,
то число этапов, которые предстоит
пройти всем заявкам системы равно
работы. Если обслуживаемая заявка
находится на -том этапе обслуживания,
то число этапов, которые предстоит
пройти всем заявкам системы равно
 — связь числа заявок с количеством
этапов обслуживания. Зная вероятность
того, что в системе имеется
— связь числа заявок с количеством
этапов обслуживания. Зная вероятность
того, что в системе имеется
 этапов
этапов
 можем вычислить вероятность наличия
заявок в системе
можем вычислить вероятность наличия
заявок в системе
 .
.
СИСТЕМА M|M|1.
В
момент времени
 поступает заявка на обслуживание. Если
система обслуживает заявки, то вновь
пришедшие становятся в очередь.
поступает заявка на обслуживание. Если
система обслуживает заявки, то вновь
пришедшие становятся в очередь.

Далее по графу состояний строим систему ДУ Колмогорова.



Найдем
решения системы, приняв
 .
Имеем
.
Имеем

 откуда
следует, что
откуда
следует, что
 .
По условию нормировки
.
По условию нормировки
 рассмотрим ряд
рассмотрим ряд
 ,
который для
,
который для
 сходится. А значит
сходится. А значит
 .
.
В
результате имеем
 .
.
МО
числа заявок, находящихся в очереди

 ,
для
.
,
для
.
МО
длины очереди

 .
Заметим, что
.
Заметим, что
 .
.
СИСТЕМА M|M|C.
 - число каналов обслуживания. Построим
граф переходов состояний системы.
Сочтоянием системы является число
заявок системы.
- число каналов обслуживания. Построим
граф переходов состояний системы.
Сочтоянием системы является число
заявок системы.

Если в системе нет очереди, то граф оканчивается на состоянии .
Запишем систему ДУ Колмогорова.



Для
стационарного режима, т.е.
 ,
вычисляем все вероятности
,
вычисляем все вероятности
 .
.


Находим из условия нормировки.
Среднее
число заявок системы равно

 ;
;
Средняя
длина очереди равна
 .
.
СИСТЕМА M|M|1|K : КОНЕЧНЫЙ НАКОПИТЕЛЬ.
В
этой системе фиксировано число ожидающих
заявок, и
 обозначает ёмкость накопителя (буфера),
поэтому любая поступившая заявка
получает отказ, если в накопителе нет
мест.
обозначает ёмкость накопителя (буфера),
поэтому любая поступившая заявка
получает отказ, если в накопителе нет
мест.
З аметим,
что
аметим,
что


Так
как по условию нормировки, то
по условию нормировки, то
 ;
;
Следовательно
 , а значит
, а значит
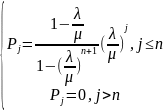 .
.
Примечание:
рассмотреть случай для
 .
.
СИСТЕМА С ПЕРЕПОЛНЯЮЩИМ ПОТОКОМ.
Время обслуживания экспоненциально, и один канал обслуживания. Входящий поток переполняет систему, т.е. заявок в системе становится все больше и больше, следовательно, возрастает очередь. Выбор интенсивности входящего потока обусловлен тем, что интенсивность поступающих заявок характеризуется гармоническим рядом в зависимости от числа заявок, находящихся в системе.


По
условию нормировки
 откуда
следует
откуда
следует
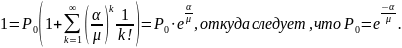

Среднее
число заявок системы равно

 ;
;
Среднее
время пребывания заявки в системе
вычислим при помощи формулы Литтла
 , где
, где
 – среднее число заявок в системе,
– обратная величина времени между
поступлением двух заявок. В результате
получим
– среднее число заявок в системе,
– обратная величина времени между
поступлением двух заявок. В результате
получим
 .
.
ПОСТРОЕНИЕ ЭМПИРИЧЕСКОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ. ОЦЕНКА ЭМПИРИЧЕСКОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ. ПОЛИГОН ЧАСТОТ.
Эмпирическая
функция распределения определяется по
формуле

 .С
другой стороны,
.С
другой стороны,
 .
.
В ысота
прямоугольников равна накопленной
относительной частоте. Ломаная,
соединяющая середины прямоугольников
называется гистограммой.
ысота
прямоугольников равна накопленной
относительной частоте. Ломаная,
соединяющая середины прямоугольников
называется гистограммой.
На
практике часто бывает известно, что
функция распределения принадлежит
определенному классу распределений,
зависящих от одного или нескольких
параметров
 ; В
этом случае становится задача определения
оценок неизвестных параметров по
выборке.
; В
этом случае становится задача определения
оценок неизвестных параметров по
выборке.
Если
имеется выборка
 ,
то число
,
то число
 – это количество выборочных значений,
попавших левее
– это количество выборочных значений,
попавших левее
 .
Тогда
.
Тогда
 и будет оценкой эмпирических значений,
где
– объем выборки. По закону больших чисел
и будет оценкой эмпирических значений,
где
– объем выборки. По закону больших чисел
 ;
;
