
- •Закон Кулона. Полевая трактовка закона Кулона.
- •Напряженность электрического поля.
- •Правила Кирхгофа.
- •Теорема Гаусса.
- •Применение теоремы Гаусса для расчета напряженности полей. Поле бесконечной заряженной плоскости.
- •Электрический ток в электролитах.
- •Теорема Био-Савара-Лапласа
- •Закон Ома для полной цепи.
- •Диэлектрики в электрическом поле. Вектор смещения.
- •Электрический ток. Закон Ома для однородного и неоднородного участков цепи.
- •Энергия электрического поля
- •Закон преломления. Абсолютный и относительный показатели преломления. Ход лучей в призме.
- •Ферромагнетики в магнитном поле. Гистерезис.
- •Линза. Формула тонкой линзы. Построение изображений в тонкой линзе.
- •Поляризация света. Закон Малюса.
- •Мощность в цепи переменного тока.
- •Работа и мощность тока.
- •Емкость уединенного проводника. Конденсаторы.
- •Электрический ток в газах.
- •Магнитное поле. Вектор индукции магнитного поля.
- •Индукция. Взаимоиндукция.
- •Магнитное поле в веществе. Вектор намагничения. Теорема о циркуляции вектора намагничения.
- •Вектор напряженности магнитного поля. Теорема и циркуляции вектора напряженности.
- •Классическая теория электропроводности.
- •Диамагнетики. Лармова прецессия.
- •Основы зонной теории проводимости.
- •Полное внутренне отражение. Предельный угол полного внутреннего отражения. Рефрактометр.
- •Поглощение света. Закон Бугера-Ламберта.
- •Дисперсия света.Спектроскоп.
- •Сила Лоренца. Масс-спектрометр. Синхрометр.
- •Глаз. Лупа. Микроскоп. Телескоп.
- •Дифракция света. Дифракционная решетка.
- •Интерференция.
Энергия электрического поля
По
современным представлениям, электрическая
энергия конденсатора локализована в
пространстве между обкладками
конденсатора, то есть в электрическом
поле. Поэтому ее называют энергией
электрического поля. Напряженность
однородного поля в плоском конденсаторе
равна E = U/d,
а его емкость
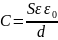 .
Поэтому
.
Поэтому
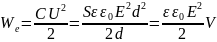
где
V = Sd
– объем пространства между обкладками,
занятый электрическим полем. Из этого
соотношения следует, что физическая
величина
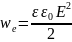 является
электрической (потенциальной) энергией
единицы объема пространства, в котором
создано электрическое поле. Ее называют
объемной
плотностью электрической энергии.
является
электрической (потенциальной) энергией
единицы объема пространства, в котором
создано электрическое поле. Ее называют
объемной
плотностью электрической энергии.
Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности wе по всему объему, в котором создано электрическое поле.
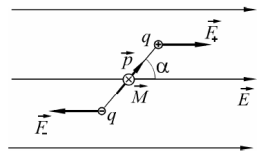
Диполь в электрическом поле. Дипольный момент.
Электрический
диполь представляет собой нейтральную
систему, состоящую из двух разноименных
по знаку равных зарядов +q
и –q,
расположенных на расстоянии l,
называемом плечом диполя. Диполь
характеризуется векторной величиной
– дипольным моментом:
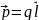 .
Вектор
.
Вектор
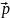 направлен отрицательного заряда к
положительному.
направлен отрицательного заряда к
положительному.
В
однородном электрическом поле
напряженностью
на диполь действует вращающий момент
пары сил
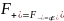 ,
который стремится повернуть диполь по
направлению внешнего поля:
,
который стремится повернуть диполь по
направлению внешнего поля:
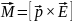 .
Модуль вращающего момента равен:
.
Модуль вращающего момента равен:
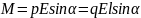 ,
где α-угол между векторами
и
.
,
где α-угол между векторами
и
.
Теорема о циркуляции вектора индукции.
Расчеты магнитного поля часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае можно пользоваться теоремой о циркуляции вектора магнитной индукции, которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике.
Поясним
понятие циркуляции вектора
 .
Пусть в пространстве, где создано
магнитное поле, выбран некоторый
условный замкнутый контур (не обязательно
плоский) и указано положительное
направление его обхода. На каждом
отдельном малом участке dl
этого контура можно определить
касательную составляющую
.
Пусть в пространстве, где создано
магнитное поле, выбран некоторый
условный замкнутый контур (не обязательно
плоский) и указано положительное
направление его обхода. На каждом
отдельном малом участке dl
этого контура можно определить
касательную составляющую
 вектора
в данном месте, то есть определить
проекцию вектора
на направление касательной к данному
участку контура.
вектора
в данном месте, то есть определить
проекцию вектора
на направление касательной к данному
участку контура.
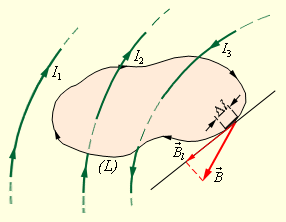
Циркуляцией
вектора
называют сумму произведений
dl,
взятую по всему контуру L:
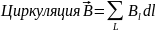
Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур L в то время, как другие токи могут находиться в стороне от контура.
Теорема
о циркуляции утверждает, что циркуляция
вектора
магнитного поля постоянных токов по
любому контуру L
всегда равна произведению магнитной
постоянной μ0
на сумму всех токов, пронизывающих
контур:
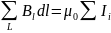
Энергия магнитного поля.
Энергия
магнитного поля, создаваемого контуром
индуктивностью L
, по которому протекает ток I
вычисляют по формуле: W=LI2/2.
Объемная плотность энергии магнитного
поля определяется из выражения
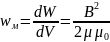 .
.
Применение теоремы о циркуляции вектора индукции.
Простейшим
примером применения теоремы о циркуляции
является вывод формулы для магнитной
индукции поля прямолинейного проводника
с током. Учитывая симметрию в данной
задаче, контур L
целесообразно выбрать в виде окружности
некоторого радиуса R,
лежащей в перпендикулярной проводнику
плоскости. Центр окружности находится
в некоторой точке проводника. В силу
симметрии вектор
направлен по касательной, а его модуль
одинаков во всех точках окружности.
Применение теоремы о циркуляции приводит
к соотношению:
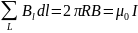 .
.
откуда следует формула для модуля магнитной индукции поля прямолинейного проводника с током.
Этот пример показывает, что теорема о циркуляции вектора магнитной индукции может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля.
Имеется немало практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является задача вычисления поля тороидальной катушки.
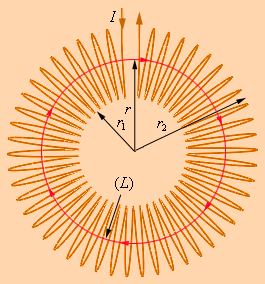
Предполагается,
что катушка плотно, то есть виток к
витку, намотана на немагнитный
тороидальный сердечник. В такой катушке
линии магнитной индукции замыкаются
внутри катушки и представляют собой
концентрические окружности. Они
направлены так, что глядя вдоль них, мы
увидели бы ток в витках, циркулирующим
по часовой стрелке. Одна из линий
индукции некоторого радиуса r1 ≤ r < r2
изображена на рис. Применим теорему о
циркуляции к контуру L
в виде окружности, совпадающей с
изображенной на рис. линией индукции
магнитного поля. Из соображений симметрии
ясно, что модуль вектора
одинаков вдоль всей этой линии. По
теореме о циркуляции можно записать:
B ∙
2πr
= μ0IN,
где N
– полное число витков, а I
– ток, текущий по виткам катушки.
Следовательно,
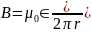 .
.
Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, то есть r2 – r1 << r, то магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае B = μ 0I n.
В это выражение не входит радиус тора, поэтому оно справедливо и в предельном случае r → ∞. Но в пределе каждую часть тороидальной катушки можно рассматривать как длинную прямолинейную катушку. Такие катушки называют соленоидами. Вдали от торцов соленоида модуль магнитной индукции выражается тем же соотношением, что и в случае тороидальной катушки.
