
- •Понятие высказывания. Простые и составные высказывания. Равные высказывания. Таблица истинности и их применения.
- •Операции над высказываниями : дизъюнкция, конъюнкция, отрицание, импликация, эквиваленция, разделительная дизъюнкция, штрих Шеффера, стрелка Пирса. Свойства.
- •Виды теорем и связь между ними. Примеры.
- •Логические задачи и логические парадоксы (антиномии).
- •Решение
- •Понятие и примеры множеств. Равные множества. Конечные и бесконечные множества. Числовые множества. Диаграммы Эйлера и их применения. Способы задания множеств.
- •Подмножества. Свойства отношения включения. Понятие булеана.
- •Операции над множествами : объединение, пересечение, вычитание, дополнение, симметрическое вычитание, декартово умножение.
- •Равномощность множеств. Примеры. Счётные множества и множества мощности континуум.
- •Бинарные отношения на множестве. Примеры. Частные виды. Особенности графов и матриц.*)
- •Отношение эквивалентности. Примеры. Класса эквивалентности.
- •Отношения порядка. Примеры.
- •Б ао как отображение МxМ м. Свойства и примеры бао.
Подмножества. Свойства отношения включения. Понятие булеана.
Множество (неопределяемое понятие) – совокупность предметов, объединенных в одну какую-л группу (прописными буквами латинского алфавита: А, В, С, ... , Z).
Множество В явл-ся подмн-вом мн-ва А, если кажд эл-т мн-ва В является также эл-том мн-ва А. Пустое мн-во считают подм-вом любого мн-ва. Любое мн-во – подмн-во самого себя. (ВА).
В: «Мн-во учеников в классе»
А: «Мн-во учеников в этом классе с короткой стрижкой». АВ.
Теорема о cв-вах отношения включения ().
1º А
2ºАА
3º Если АВ и ВС, то АС (транзитивность)
Док-во 3º: Условие: АВ, ВС.
Возьмем аА Т.к. АВ, аВ (явл-ся Эл-том мн-ва В)
Т.к. ВС, аС. Значит АС.
4º критерий (необходимый и достаточный признак) равенства мн-в А=В iff АВ и ВА.
Док-во обратного утв-я от противного. Если бы АВ, то например, в А есть эл-т а, который не явл-ся эл-том В. Но это не противоречит условию АВ.
Если АВ, то в В есть Эл-т, которого нет в А.
Буль Джордж (1815-1864)
Опр.: Булеан множества А – это множ-во ß(А), состоящее изо всех подмножеств множ-ва А.
Exx:
1)Для А=![]() его численность |A|=0, а булеан ß(А)={
}-
состоит из 1 эл-та –пустого множества
его численность |A|=0, а булеан ß(А)={
}-
состоит из 1 эл-та –пустого множества
2) Для А={1}, |A|=1, ß(А)={ , {1}} , 3) Для А={1,2}, |A|=2, ß(А)={ , {1}, {2}, {1,2}} , 4) Для А={1,2, 3}, |A|=3, ß(А)={ , {1}, {2},{3},{1,2}, {2,3}, {1,3},{1,2,3}} состоит из 8 эл-ов.
Теорема
о числ-ти булеана: | ß(А)|=2 в степени |А|
, Док-во: Пусть |А| =n. Введем описание
подмножества в виде поломки из n клеточек
![]() (В
кажд. клетке либо 1 либо 2. 3 кл-ки-2 в
3-ейстепени=8 способов заполнения)
(В
кажд. клетке либо 1 либо 2. 3 кл-ки-2 в
3-ейстепени=8 способов заполнения)
При помощи нулей и единиц можно описать любое подмножество. Например: все нули-это пустое подмножество, все единицы- само множ-во А. Единица но 1-ом месте, остальные нули – это {a с индексом 1}. Ск-ко описаний, столько и подмножеств, а их число (описаний) равно 2в степени n, т. к. каждую клеточку можно заполнить 2-мя способами.
Операции над множествами : объединение, пересечение, вычитание, дополнение, симметрическое вычитание, декартово умножение.
Множество (неопределяемое понятие) – сов-ть предметов, объединенных в одну какую-л группу.
Мн-во В явл-ся подмн-вом мн-ва А, если кажд эл-т мн-ва В явл-ся также эл-ом мн-ва А. считают подм-вом любого мн-ва. Любое мн-во – подмн-во самого себя. (ВА).В: «На 4 и 5» А: «с коротк стрижкой».
Пересеченuем мн-в А u В наз мн-во, содержащее те u только те эл-ты, кот прuнадлежат мн-ву А u мн В.
А В = {х I х Е А и х Е В}.Если изобраз мн-ва А и В с пом кругов Эйлера, то -ем дан мн-в явл заштрих обл.
![]() в
том случ, когда мн-ва А
и
В
не
им общих эл-тов, говорят, что их -е
пусто: А
В
=
.
в
том случ, когда мн-ва А
и
В
не
им общих эл-тов, говорят, что их -е
пусто: А
В
=
.
А – мн-во четн натур чисел В – мн-во двузн чисел.
Характеристическое св-во эл-тов мн-ва А-«быть четн натур числом»,В - «быть двузн числом».Т.О, мн-во
А В сост из четн двузн чисел. Полученное мн-во не пусто.Н-р, 24 АВ, п.ч. число 24 четн и двузн.
А-мн-во всех ромбов, В –прямоуг. АВ-квадратов.
Теорема о cв-вах пересечения.
1ºАВ=ВА (коммутат) 2º(АВ)С=А(ВС) (асс)
3º АА=А (идемпотентность) 4º А=
5ºЕсли АВ, то АВ=А (меньшему из них)
6º (АВ) С=(АС)(ВС) (дистрибутивность -я отн-но объединения) 7º (АВ) С=(АС) (ВС)
8º(АВ) А=А 9º (АВ) В=А }з-ны поглощения
Объединением мн-в А и В наз мн-во, содержащее те и только те эл-ты, кот принадл хотя бы 1 из этих мн-в.
![]() А=
{1,2,3} В={3,4,5}
А=
{1,2,3} В={3,4,5}
АВ={1,2,3,4,5}Эл-т не может встречаться дважды.
А=N, В={0} АВ= N0 -мн-во целых неотриц чисел.
Теорема о cв-вах объединения.
1ºАВ= ВА (коммут) 2º(АВ) С=А(ВС) (асс)
3º АА=А (идемпотентность) 4º А=А
5º Если АВ, то АВ=В (большему из них)
Док-во 5º: Усл: АВ Док-ть АВ=В Докажем сначала, что В АВ – это очевидно (по опр.),
Докажем обратное вкл-е: АВВ. Пусть х АВ, тогда хА или хВ. Если хА, то с учетом дано хВ.
Если хВ, то хВ. Во всех случаях х явл-ся эл-том В (хВ) ч.т.д.По критерию равенства мн-в АВ=В ч.т.д.
Разностью (А\В) мн-в А и В наз А\В состоящая из тех и только тех эл-тов мн-ва А, кот. не явл-ся эл-тами В.
![]()
![]()
Теорема о cв-вах вычитания.
1º А\ =А ( – прав нейтральный эл-т вычитания)
2º \ А= 3º А\А= 4ºА\В=А\(АВ)
5ºА\ (АВ)= 6º А\ (А\В)= АВ=В\ (В\А)
7º А\ (В\А)=А 8º (А\ В) А, (А\В) В=АВ.
Симметрической разностью мн-в А и В наз мн-во АВ, состоящее из тех и только тех эл-тов, которые или мн-ву А или мн-ву В.
![]() Теорема
о cв-вах симм. вычит.
Теорема
о cв-вах симм. вычит.
1ºАВ=ВА 2º(АВ)С=А(ВС) (ассоц)
3ºАА= 4ºА=А 5ºА (АВ)=В
6º АВ = (АВ)\ (АВ)=(А\ В) (В\ А)
Дополнением мн-ва В до мн-ва А наз мн-во, содерж те и только те эл-ты мн-ва А, кот не принадлеж мн-ву В.
![]() Дополнение
мн-ва
до универсального.
Дополнение
мн-ва
до универсального.
Пусть U- универсальное мн-во. Все мн-ва его подмн-ва. Тогда для подмн-ва универсального мн-ва U его дополнением Ā наз Ā= U\А.
Теорема о cв-вах дополнения.
1º двойное отрицание А=А (инволютивность)
2º отрицание АВ= Ā отрицание В }з-ны
3º А В= Ā отрицание В де Моргана
4º А Ā = U 5º = U 6º отрицание U =
Декартовым умножением мн-в А и В наз мн-во АВ, состоящее из всех упорядоченных пар (а,b), где а А, bВ. Можно перечислить пары или взять 2 мн-ва.
А={2,3,5} В = {-1, 0,4,6} АВ = {(2,-1), (2,0), (2,4), (2,6), (3,-1), (3,0), (3,4), (3,6), (5,-1), (5,0), (5,4), (5,6) }.
Изображение декартова произведения числовых множеств.
Из фотографий лекций – рис 27
Теоремы о численности множеств. Задачи.
Т еорема:
(для 2-х множеств) | AUB|+ |AUB|=|A|+|B|. Док-во:
Если сложитьA| и |B|, то сумма будет больше
| AUB| на | AUB|, т.к. эл-ты пересечения были
сосчитаны дважды.
еорема:
(для 2-х множеств) | AUB|+ |AUB|=|A|+|B|. Док-во:
Если сложитьA| и |B|, то сумма будет больше
| AUB| на | AUB|, т.к. эл-ты пересечения были
сосчитаны дважды.
Теорема
для 3-х множеств: |AUBUC|=|A|+|B|+|C|-
|A![]() B|-|B
C|-|C
A|+|A
B
C|
B|-|B
C|-|C
A|+|A
B
C|
Д оказательство:Если
сложить ||A|, |B|, |C|, то сумма будет больше
модуля |AUBUC| на |A
B|+|B
C|+|C
A|
поэтому эту сумму надо вычесть. Однако
при этом элементы из А
B
C
не будут учтены ни разу(сначала их
трижды сосчитали, а потом вычли), поэтому
надо прибавить ||A
B
C|,
тогда получим |AUBUC|.
оказательство:Если
сложить ||A|, |B|, |C|, то сумма будет больше
модуля |AUBUC| на |A
B|+|B
C|+|C
A|
поэтому эту сумму надо вычесть. Однако
при этом элементы из А
B
C
не будут учтены ни разу(сначала их
трижды сосчитали, а потом вычли), поэтому
надо прибавить ||A
B
C|,
тогда получим |AUBUC|.
Задача: В группе 30 человек, кот-е изучают английский, немецкий, французский и китайский языки. 15 чел. изучают англ. яз., 14 –нем., 13-французский. Англ. и нем. изучают 9, нем. и фр.-8, фр. и англ. -7 чел. , 3-е изучают 3 эти языка (англ., нем., фр.) Есть ли студенты, изучающие только немецкий? Только китайский язык? Сколько их? А также изучающих по одному или по 2 европейских языка? По одному языку? Решение: 30.
Замечание: можно понимать, что 9 человек изучают англ. и нем. без фр. , а можно с францезским.
В 1-ом случае (рис. выше): 9,8,7,3. Во 2-м случае-
что же делать?(будем писать в центре 3,
а дальше 6, 5, 4). Мы заметим, что 1-ый случай
не может иметь места.(условие можно
понимать только как 2-ой случай). Т.о.
Т.к. |E
D|=9,то
|E
D
не
F|=9-3=6(чел. изучают англ. и нем. и не изучают
французский).
1-ом случае (рис. выше): 9,8,7,3. Во 2-м случае-
что же делать?(будем писать в центре 3,
а дальше 6, 5, 4). Мы заметим, что 1-ый случай
не может иметь места.(условие можно
понимать только как 2-ой случай). Т.о.
Т.к. |E
D|=9,то
|E
D
не
F|=9-3=6(чел. изучают англ. и нем. и не изучают
французский).
Аналогично |D F не Е|=8-3=5(изуч. нем. и фр. но не изуч. англ. яз.), |F E не D|=7-3=4(не изуч. нем.)
После этого ищем тех, кто изучает только английский: |E неD не F|=15-(6+4+3) = 2, только немецкий язык:
|D не F не Е|=14-6-5-3=0-таких студентов нет. Изучающие только французский: | F не D не Е|=13-4-5-3=1.
После этого находим: |не E неD не F|=30-15-1-0-5=9- они изучают китайский язык. Только нем. не изучает никто.
Тождественные преобразования в алгебре множеств.
Основные понятия. Примеры.
Говорят, что между мно-вами А и В задано соответствие f, если хотя бы одному элементу из А соответствует что-то из В.
a f b (b=f(a), a→b). элементу а из А по закону f соответствует b из В.
Множество всех преобразований называется областью определения соответствия f и обозначается D(f).
Г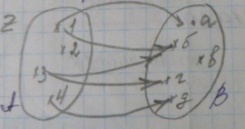 раф
соответствия f
– это
раф
соответствия f
– это
Мы видим, что 1 f a, 1 →б, б=f(3), 3fг, 4fд, а также, что D(f) = {1,3,4}, E(f) = {а, б, г, д}.
Понятно, что (область определения часть) D(f) c A, E(f) c B.
График соответствия f – это множество G(f) всех пар вида (a.b), где a f b. Понятно, что G(f) c AxB
У нас G(f) = {(1,a), (2, б), (3, г), (4, д)}
Частные виды соответствий: всюду определённые, сюръекции, функции, инъекции (а также отображения и биекции). Особенности графов и матриц.
Обратные соответствие f -1 и его свойства.
О композиции f о g соответствий f и g. Ассоциативность композиций.
Примеры биекций . свойства биекций.
Определения. 1) Если f одновременно всюду определено и функция, то f – отображением A в B. (На графе: из каждой точки A только одна стрелка. f – всюду определенное (D(f)=A. На графе: из каждой точки A должна выходить хотя бы одна стрелка.)).
2) Соответствие f – биекция (f одновременно сюръекция, функция и инъекция (равночисленность множеств). f – сюръекция (E(f)=B. На графе: к каждой точке B должна подходить хотя бы одна стрелка). f – функция (у каждого элемента из A не более одного образа в B (1 или 0). На графе: из каждой точки A выходит не более 1 стрелки). f – инъекция (у каждого элемента из B не более 1 прообраза в A. На графе: к каждой точке B подходит не более 1 стрелки).).
Примеры биекции: 1) Если f – биекция между конечными множествами A и B, то можно понять, что эти множества должны быть равночисленными (|A|=|B|).
2) N: 1, 2, 3, 4, 5, …; N0: 0, 1, 2, 3, 4, …; f(n)=n-1 (биекция) не трудно убедиться, что f – биекция, проверяем является ли оно сюръекцией, функцией и инъекцией).
3) N: 1, 2, 3, 4, 5, …; N2: 2, 4, 6, 8, 10, …; f(n)=2n (биекция)
4) N и веревка с узлами. Биекция между N и узлами этой веревки устанавливается легко.
