16

ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ (МКТ) СТРОЕНИЯ ВЕЩЕСТВА. Лекция II.

«РАВНОВЕСНЫЕ РАСПРЕДЕЛЕНИЯ МОЛЕКУЛ»

#1 Понятие распределения молекул.

В предыдущей лекции говорилось о распределениях микросостояний макросистемы. При этом средняя скорость одной конкретной молекулы, например, первой, при данном распределении равна

,

где i  индекс микросостояния, _i – вероятность его появления. Но если все молекулы физически равноправны, то, найдя среднюю скорость одной молекулы, мы найдем средние скорости каждой из молекул. Поэтому должен существовать способ выражения без ссылок на конкретную микрочастицу. Иными словами, мы должны научиться выражать через вероятности _i механических состояний всей системы вероятности одночастичных характеристик.

Записывая выражение , мы как бы «примеряли» различные векторы скорости частицы на частицу №1. Но ведь можно сделать наоборот, заняться «примеркой» различных частиц на данный вектор скорости . Т.е. вместо вопроса, «какой вектор скорости у частицы №1 в микросостоянии i?» можно задать вопрос: «как много частиц обладает скоростью в микросостоянии i?». Ответом будет так называемое число заполнения вектора в i-ом микросостоянии: . Более того, зная, что механическое состояние одной частицы определяется не только скоростью, но и положением, можно задать вопрос: «каково число заполнения одночастичного механического состояния в данном микросостоянии, т.е. чему равно ?». Абсолютно очевидно, что числа заполнения являются механическими характеристиками микросостояний и их можно усреднять. Тогда среднее число заполнения одночастичного состояния в данном макросостоянии

.

С другой стороны, в случае равновесного ТД состояния изолированной системы по эргодической теореме:

.

Если количество частиц в системе N  как бы общее число граней игральных костей, то число частиц в состоянии в данный момент времени - как бы число «нужных» граней игральной кости, выпавших «в этот раз». Тогда - эмпирически измеренная вероятность того, что произвольная частица будет находиться в состоянии . Т.е. по закону игральных костей, бросаемых бесконечное количество раз, - это, как раз, та вероятность , выражение которой мы и искали. Следовательно, ответом на вопрос о средней скорости любой частицы в равновесном ТД состоянии является формула:

.

Но эта формула имеет натяжку: в правой части стоит знак дискретного суммирования, применяемого тогда, когда индекс, по которому оно производится, является дискретным. В формуле роль индекса играет сочетание векторов , ни один из которых не является дискретным. Значит, правильно будет суммирование заменить интегрированием, а вместо дискретной вероятности иметь дело с дифференциалом вероятности , в котором среднее число заполнения одночастичного состояния заменяется на среднее число заполнения окрестности одночастичного состояния . В случае непрерывного аргумента появление у произвольной частицы точного состояния не может быть событием с ненулевой вероятностью. Таким событием оказывается появление у произвольной частицы состояния в окрестности , и эта окрестность имеет вид , где в случае декартовой системы координат  малый объём «реального» пространства вблизи точки ,

а является малым объёмом пространства скоростей вблизи вектора .

Тогда вероятностью произвольной частице системы находиться вблизи одночастичного состояния , является малая величина

,

где функция называется функцией плотности вероятности того, что произвольная частица находится в механическом состоянии . При этом среднее число заполнения окрестностей имеет вид:

.

Функция называется функцией распределения частиц системы по механическим состояниям .

Естественно, можно ввести функцию распределения частиц по положениям:

,

где интегрирование ведётся по всему пространству скоростей. Очевидно, что связана с функцией плотности вероятности того, что произвольная частица находится в положении :

.

И точно также можно определить функцию плотности вероятности того, что произвольная частица будет обладать скоростью . Здесь интегрирование ведётся по всему объёму, занятому макротелом. А через эту функцию можно выразить функцию распределения частиц по скоростям:

.

Подведём итог. Дифференциал вероятности появления какой-либо микрочастицы системы вблизи данного одночастичного механического состояния известным образом выражается через условные вероятности микросостояний всей системы, о которых нам известно только то, что они связаны с равновесным макросостоянием. С другой стороны, дифференциал вероятности выражается с помощью плотности вероятности по одночастичным состояниям или по их составным частям (положениям или скоростям). Эти плотности вероятности, таким образом, определяются макросостоянием системы, но пока неизвестно как. Зато мы знаем, что с их помощью находятся функции распределения частиц данной макросистемы.

#2 Вывод уравнения состояния идеального газа.

Теперь, вооружившись аппаратом классической статистической физики, мы применим его для решения наиболее простого вопроса: описания идеального газа. Нас будет интересовать вопрос выражения его внутреннего параметра – давления. Как известно, давление р равно , где - нормальная составляющая силы , действующей на площадь . Но, может быть, не всем известно, что является скоростью передачи импульса элементу поверхности , т.е. равно отношению количества импульса , переданного элементу в течение времени , к этому промежутку времени:

.

Если стенка, которой принадлежит , «бомбардируется» частицами газа, то импульс передаётся в отдельных актах соударений частиц со стенкой. Мы будем считать, что удар упругий о гладкую поверхность. И тогда порция импульса, переданная в одном акте соударения частицей, имеющей скорость и обладающей массой т₀ будет иметь вид:

,

где  - угол падения.

Количество частиц, имеющих скорость и попадающих на поверхность в единицу времени называется элементарным потоком частиц:

,

где - вектор плотности потока частиц, обладающих скоростью , а - концентрация таких частиц. Тогда

.

С элементарным потоком частиц связан элементарный поток нормального импульса

.

Это – количество нормального импульса, переданного поверхности со стороны частиц, обладающих скоростью , в единицу времени. Следовательно,

.

Исходя из #1

.

Таким образом,

.

Полный поток импульса связан со всеми скоростями , направленными к поверхности под острым углом :

(интегрирование по полупространству пространства скоростей). В силу изотропности распределения частиц по скоростям в состоянии теплового равновесия интеграл по полупространству равен половине интеграла по пространству:

,

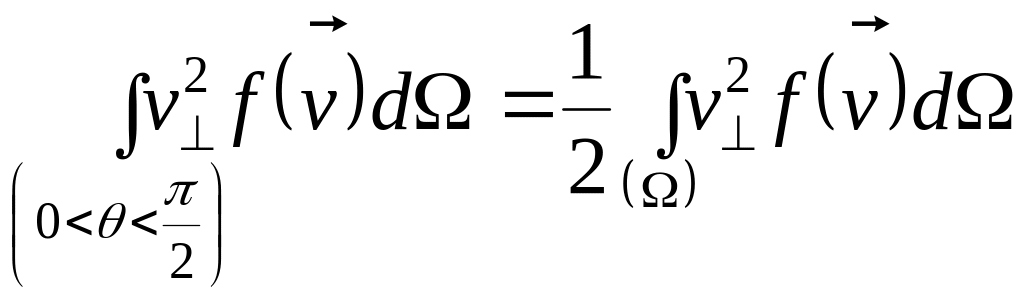а последний интеграл равен - среднему квадрату составляющей скорости, перпендикулярной . Следовательно,

.

Направим ось z перпендикулярно поверхности dS (т.е. параллельно ). Тогда = , но из-за изотропности распределения по скоростям оси z,y,x равноправны (y,x лежат в плоскости ). Следовательно,

.

Тогда

,

следовательно,

Мы рассмотрели ситуацию в одной точке пространства, заполненного газом: вблизи элемента поверхности (не обязательно оболочки). Но в силу однородности идеального газа по всему объёму, заполненному им, в состоянии ТД-равновесия концентрация п и средний квадрат скорости одинаковы по всему объёму, следовательно, в любой точке идеального газа

.

Это - основное уравнение МКТ идеального газа.

По теореме о равном распределении:

,

следовательно, , т.е.

Вывод уравнения состояния идеального газа на основе МКТ явился основным аргументом в пользу её справедливости, предложенным физиками.

#3 Распределение Максвелла

Это – распределение молекул идеального газа по скоростям. Понятно, что вопрос сводится к определению плотности вероятности скорости произвольной частицы .

Максвелл догадался о том, каков вид этой функции, исходя из следующих соображений.

1. Предположение о независимости распределений молекул по проекциям скоростей:

2. Изотропность распределения. Из неё следует:

.

Из 1,2 получаем

.

Такое соотношение возможно, только если

;

;

.

При этом коэффициенты положительны, т.к. иначе расходятся, а нужно, чтобы эти интегралы по смыслу плотности вероятности были равны 1. Тогда

,

где С=С₁³, =₁ в силу равноправия осей. Это, собственно, и есть закон распределения Максвелла по скоростям. Для полного его описания необходимо знать С и .

Возвратимся к функциям распределения по проекциям:

По определению плотности распределения, её интеграл по всем проекциям скорости должен быть равен 1:

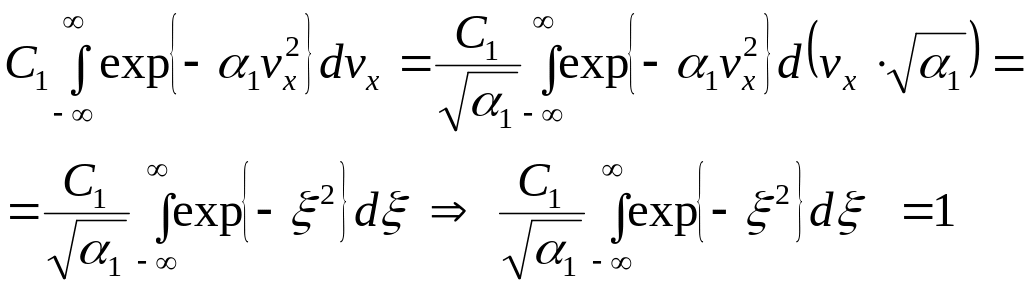
Входящий сюда интеграл называется интегралом Пуассона. Он равен . Следовательно,

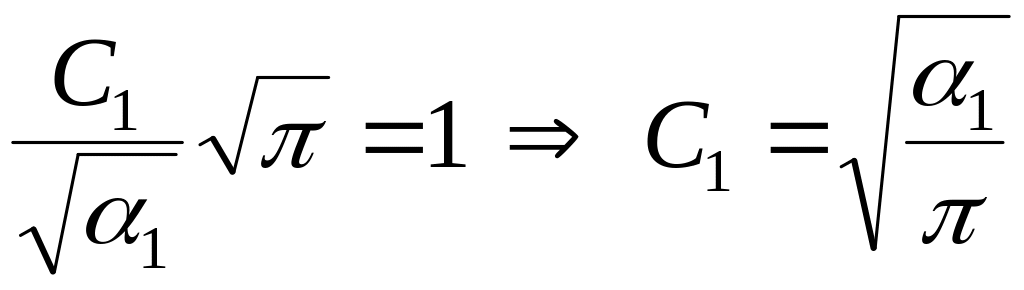т.е.

Средняя кинетическая энергия вдоль оси х:

Подинтегральное выражение можно преобразовать:

.

Следовательно, интеграл можно взять по частям:

.

Первое слагаемое равно 0, а второе , следовательно,

.

С другой стороны по теореме о равнораспределении:

.

В результате получается:

;

Следовательно,

.

Очевидно, что

,

где - кинетическая энергия молекулы.

#4. Следствия из распределения Максвелла

• Распределение по величинам скоростей.

Вероятность того, что величина скорости произвольной молекулы имеет значение в интервале (v, v+dv) связано со сложением вероятностей по тонкому шаровому слою пространства скоростей радиусом v и толщиной dv.

• Наиболее вероятная скорость.

Функция распределения по величинам скоростей имеет максимум т.к. она положительна, и , .

Решим уравнение :



• Средняя скорость.

Понятно, что здесь вся трудность – во взятии интеграла.

Так же, как делали раньше: преобразуем подинтегральное выражение:

.

Следовательно, интеграл можно взять по частям:

Теперь, если собрать всё, получим:



• Среднеквадратичная скорость.

По определению:

.

Понятно, что



• Распределение по энергиям.

Вернемся к выражению дифференциала вероятности по величине скорости:



#5. Распределение Больцмана.

5.1 Распределение молекул по классическим одночастичным состояниям.

Как следует из предыдущего параграфа, функция плотности вероятности того, что молекула идеального газа имеет определённую скорость, связана с кинетической энергией, соответствующей этой скорости:

,

где множитель перед экспонентой не зависит от данного одночастичного состояния, а определяется характеристиками системы в целом: массой молекулы и температурой системы.

Больцман, ознакомившись с видом функции , предложенной Максвеллом для идеального газа, сделал обобщение: если распределение по скоростям связано с распределением по кинетическим энергиям, то распределение по одночастичным механическим состояниям должно определяться распределением по механическим энергиям, аналогичным распределению Максвелла:

,

где механическая энергия одной молекулы

.

Постоянный множитель, стоящий перед экспонентой не зависит от одночастичного состояния, а определяется свойствами макросистемы в целом и её ТД-состоянием.

5.2 Барометрическая формула.

Если верно предположение Больцмана, то

.

Следовательно, распределение по одночастичным механическим состояниям , где

.

Самый простой случай, когда потенциальная энергия линейно зависит от одной координаты частицы, реализуется в поле тяжести Земли:

,

где z – высота над нулевым уровнем. Тогда плотность вероятности будет иметь вид:

.

Среднее число молекул газа, находящееся на данной высоте относительно нулевого уровня:

.

Обозначив постоянный множитель перед экспонентой через С и поделив на объём dV получим

выражение концентрации молекул на высоте z.

При z=0 имеем равенство: С=п(0)=п₀ – концентрация молекул на 0-й высоте. Следовательно, зависимость концентрации молекул от высоты над нулевым уровнем (уровнем моря):



 барометрическая формула Больцмана.

Соответствует ли она действительности? Подойдём к проблеме зависимости концентрации молекул идеального газа от высоты с гидростатической точки зрения. Рассмотрим столб идеального газа в поле тяжести Земли при одинаковой температуре. Выделим один элемент столба высотой dz и рассмотрим его динамическое состояние:

,

и, сократив на dS, получим:

.

Учтём связь между концентрацией и давлением идеального газа:

.

Т.е. гидростатика полностью подтверждает гипотезу Больцмана. Для произвольной зависимости распределение концентрации по Больцману имеет вид:

,

где п₀ – концентрация в точке начало отсчета потенциальной энергии.

5.3.Обобщение распределения Больцмана на случай произвольной подсистемы, являющейся частью равновесной макросистемы.

В этом пункте нам необходимо опять поменять взгляд «со стороны одночастичного состояния» на взгляд со стороны конкретной частицы. Т.е. опять заняться «примеркой» различных механических состояний на конкретные частицы.

Из распределения Больцмана следует, что вероятность реализации определённого одночастичного механического состояния в равновесном газе определяется механической энергией одночастичного состояния и температурой газа т.к. пропорциональна . Но это значит, что у конкретной молекулы то или иное одночастичное состояние появляется с вероятностью также пропорциональной этой величине (чем чаще молекулы попадают в одночастичное состояние, тем чаще это состояние реализуется на конкретной молекуле).

Любая молекула газа является частью макротела «газ». Положение о пропорциональности вероятности данной молекуле находиться в одночастичном состоянии величине можно обобщить на произвольную механическую систему, являющуюся составной частью макросистемы. Тогда вероятность появления того или иного механического состояния подсистемы в данном равновесном макросостоянии

.

Здесь Е_мех – механическая энергия подсистемы, определяемая совокупностью её динамических переменных; – «окрестность» совокупного пространства динамических переменных вблизи того их набора, который определяет Е_мех. В дальнейшем я буду называть такое пространство фазовым пространством подсистемы, а – элементарным объёмом фазового пространства. Для одной молекулы, например, фазовым пространством будет 6-ти мерное пространство . Если ввести коэффициент пропорциональности, не зависящий от механического состояния подсистемы, то последнее соотношение превратиться в равенство:

.

Интегрирование равенства по всему фазовому пространству подсистемы в левой части даёт единицу:

.

Интеграл, стоящий в знаменателе называется статистической суммой подсистемы:

.

Следовательно,

.

Например, для молекулы полярного диэлектрика в электрическом поле фазовым пространством будет совокупность возможных ориентаций дипольного момента , а W_мех – энергия ориентации относительно напряжённости электрического поля : , как было в курсе электромагнетизма. Аналогичная ситуация магнитного момента атома парамагнетика в магнитном поле, чья энергия ориентации относительно магнитной индукции определяется формулой:

На самом деле мы, таким образом, получили выражение вероятности реализации механического состояния произвольной макросистемы:

.

Последняя формула является ответом на вопрос, поставленный в #1: так определяются условные вероятности реализации того или иного микросостояния в данном равновесном макросостоянии.

#6. Статистический смысл энтропии.

Если до сих пор речь шла об условных вероятностях , то в данном параграфе мы будем иметь дело с безусловной вероятностью реализации микросостояния, т.е. с вероятностью попадания системы в определённую точку фазового пространства безотносительно к её макросостоянию. Статистическая физика постулирует безусловную равновероятность всех микросостояний данной системы.

Каждое макросостояние реализуется через совокупность микросостояний. Одни макросостояния «поддерживаются» большим количеством микросостояний, другие  малым.