
Ограниченные и неограниченные последовательности
Поскольку последовательности являются числовыми множествами, то естественно ввести понятие их ограниченности, как это было сделано для множеств в параграфе 1.4.
■ Определение
2. Последовательность
называется
ограниченной
сверху
(снизу), если
существует такое число М
(число
т),
что
любой элемент
этой
последовательности удовлетворяет
неравенству
 ).
).
■ Определение
3. Последовательность
называется
ограниченной,
если
она ограничена и сверху и снизу, т.е.
существуют такие числа т
и
М,
что
любой элемент
этой
последовательности удовлетворяет
неравенствам
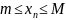 .
.
Пусть
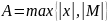 ,
тогда
условие ограниченности последовательности
можно записать в форме
,
тогда
условие ограниченности последовательности
можно записать в форме
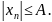
■ Определение
4.
Последовательность
называется неограниченной,
если
для любого положительного числа А
существует
элемент
,
этой
последовательности, удовлетворяющий
неравенству
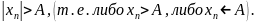
Из
определений 2—4 следует, что все элементы
ограниченной сверху
последовательности принадлежат
промежутку
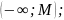 а
ограниченной
снизу — лежат на промежутке
а
ограниченной
снизу — лежат на промежутке
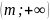 .
Неограниченная последовательность
может быть ограничена сверху (снизу).
Все элементы ограниченной
последовательности принадлежат отрезку
.
Неограниченная последовательность
может быть ограничена сверху (снизу).
Все элементы ограниченной
последовательности принадлежат отрезку
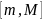 .
.
Рассмотрим несколько примеров последовательностей.
Последовательность
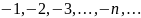 не
ограничена снизу, но
ограничена сверху.
не
ограничена снизу, но
ограничена сверху.Последовательность
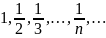 ограничена, так как любой
элемент
этой
последовательности удовлетворяет
неравенствам
ограничена, так как любой
элемент
этой
последовательности удовлетворяет
неравенствам
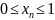 .
.
3) Последовательность
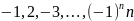 неограниченная. Действительно, каково
бы ни было число
неограниченная. Действительно, каково
бы ни было число
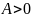 ,
среди элементов
этой
последовательности
найдутся элементы, для которых будет
выполняться
неравенство
,
среди элементов
этой
последовательности
найдутся элементы, для которых будет
выполняться
неравенство
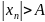 .
.
Бесконечно большие и бесконечно малые последовательности
■ Определение
5. Последовательность
называется
бесконечно
большой,
если
для любого положительного числа А
существует
такой номер
N,
что при
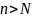 (для
всех элементов последовательности с
номерами
выполняется неравенство
.
(для
всех элементов последовательности с
номерами
выполняется неравенство
.
Очевидно,
что любая бесконечно большая
последовательность является
неограниченной. Обратное утверждение
неверно: неограниченная последовательность
может и не быть бесконечно большой.
Например, неограниченная
последовательность 1, 2, 1, 3, 1, 4, ..., 1, n,
...
не
является
бесконечно большой, так как при
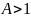 неравенство
не выполняется
для всех элементов
с нечетными
номерами.
неравенство
не выполняется
для всех элементов
с нечетными
номерами.
■ Определение
6.
Последовательность
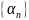 называется
бесконечно малой,
если для любого положительного числа
называется
бесконечно малой,
если для любого положительного числа
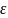 существует
такой номер
N
, что при
выполняется
неравенство
существует
такой номер
N
, что при
выполняется
неравенство
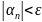 .
.
Приведем примеры бесконечно больших и бесконечно малых последовательностей.
Докажем, используя определение 5, что последовательность {n} является бесконечно большой. Возьмем любое число . Из неравенства
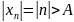 получаем
получаем
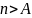 .
Если выбрать
.
Если выбрать
 ,
то для всех
будет
выполняться неравенство
.
,
то для всех
будет
выполняться неравенство
.Докажем, что последовательность
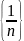 является
бесконечно малой. Возьмем произвольное
число
является
бесконечно малой. Возьмем произвольное
число
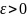 . Из неравенства
определения
6 получаем, что
. Из неравенства
определения
6 получаем, что
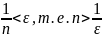 .
Если принять
.
Если принять
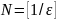 ,
то для
всех
будет
выполняться неравенство
,
то для
всех
будет
выполняться неравенство
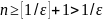 ,
т.е.
,
т.е.
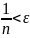 .
Тогда, согласно определению 6,
последовательность
является
бесконечно малой.
.
Тогда, согласно определению 6,
последовательность
является
бесконечно малой.
Теперь докажем теорему, устанавливающую связь между бесконечно малыми и бесконечно большими последовательностями.
▼ Теорема
2.1. Если
— бесконечно большая последовательность
и
все ее члены отличны от нуля, то
последовательность
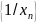 бесконечно
малая. Если все элементы бесконечно
малой последовательности
бесконечно
малая. Если все элементы бесконечно
малой последовательности
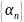 отличны
от нуля, то последовательность
отличны
от нуля, то последовательность
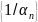 бесконечно
большая.
бесконечно
большая.
Доказательство.
Пусть
— бесконечно большая последовательность.
Для произвольно взятого числа
положим
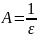 .
Согласно
определению
5, для этого А
существует
такой номер N,
что при
выполняется
неравенство
.
Отсюда
получаем:
.
Согласно
определению
5, для этого А
существует
такой номер N,
что при
выполняется
неравенство
.
Отсюда
получаем: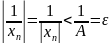 для
всех
,
т.е. последовательность
является бесконечно малой,
согласно определению 6.
для
всех
,
т.е. последовательность
является бесконечно малой,
согласно определению 6.
Доказательство второй части теоремы проводится аналогично. ▲
