Решение:

а)

б) Составим уравнение прямой АВ с помощью формулы

- уравнение прямой АВ

Уравнение высоты СD можно записать как уравнение прямой, проходящей через точку С и перпендикулярной к прямой АВ, имеющей нормальный вектор , который для этой прямой будет направляющим

СD:

Найдем точку Д, как точку пересечения прямых СД и АВ

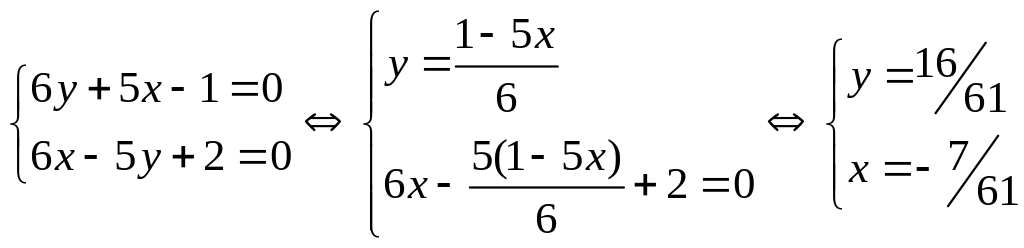
в) Медиана делит стороны ВС пополам, поэтому из формул середины отрезка

находим координаты точки М

M (7.5;3)

Уравнение прямой АМ:

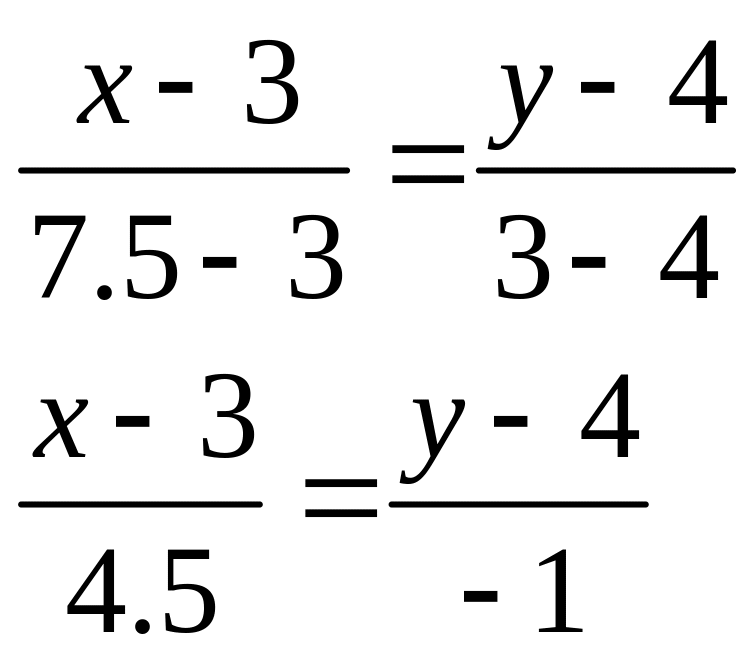
г) Точку пересечения находим из системы

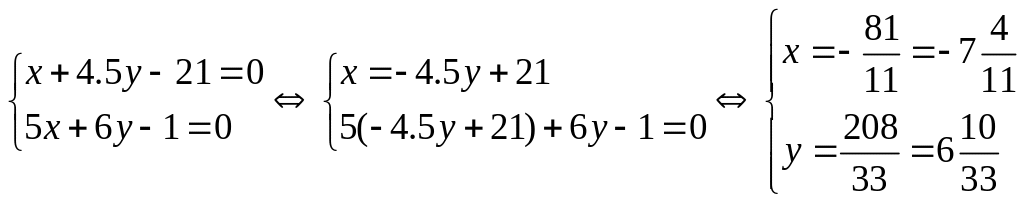
Значит, m пересечения

Задача 7. Даны четыре точки А(4,2,5), В(0,7,2), С(0,2,7) и S(1,5,0).

Найти: уравнения

а) плоскость АВС

б) прямой АВ

в) прямой SN, перпендикулярной к плоскости АВС

г) косинус угла между плоскостями АВС и ВСS

д) объем пирамиды АВСS

е) уравнение прямой SD параллельной прямой АВ

ж) площадь грани АВС

Решение:

а) Уравнение плоскости, проходящей через 3 точки

Принимает вид:

,

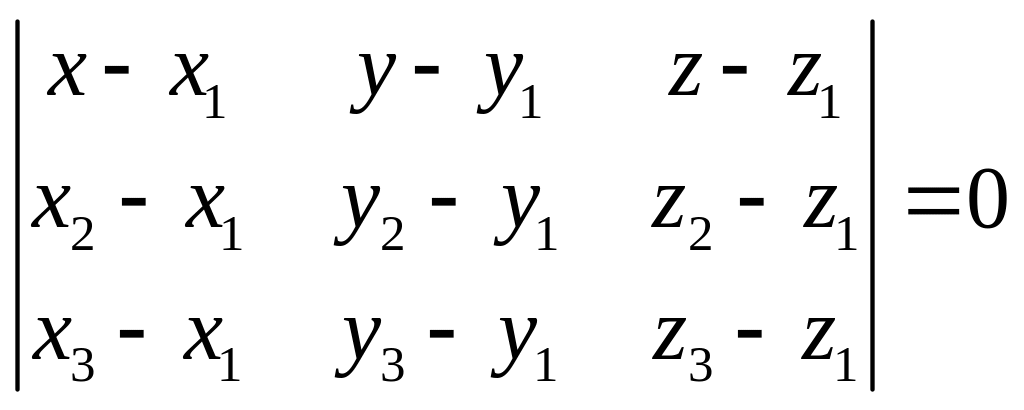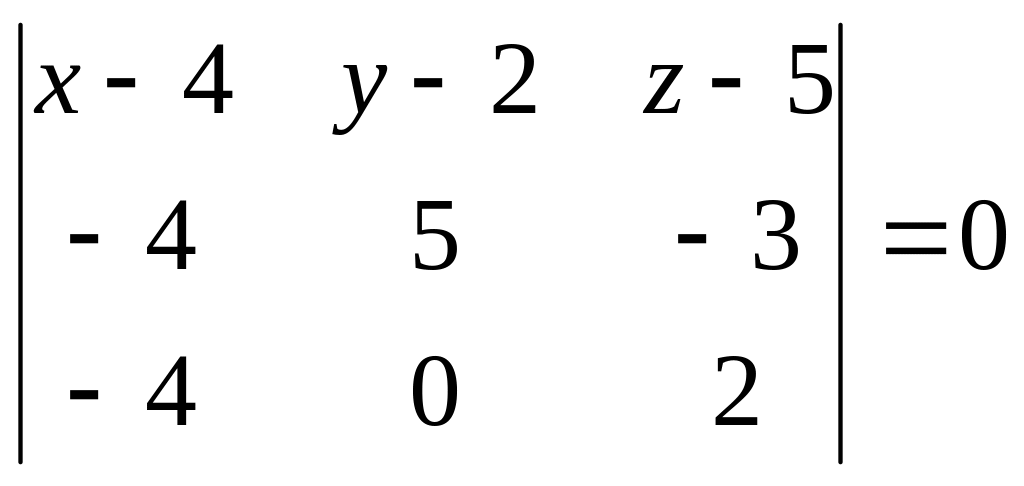
б) Уравнение прямой АВ, как прямой, проходящей через две точки, запишется так

в) Уравнение высоты SN, опущенной из вершины S на плоскость АВС можно записать как уравнение прямой, проходящей через точку S и перпендикулярной плоскости АВС, имеющей нормальный вектор , который для этой прямой будет направляющим

SN: или

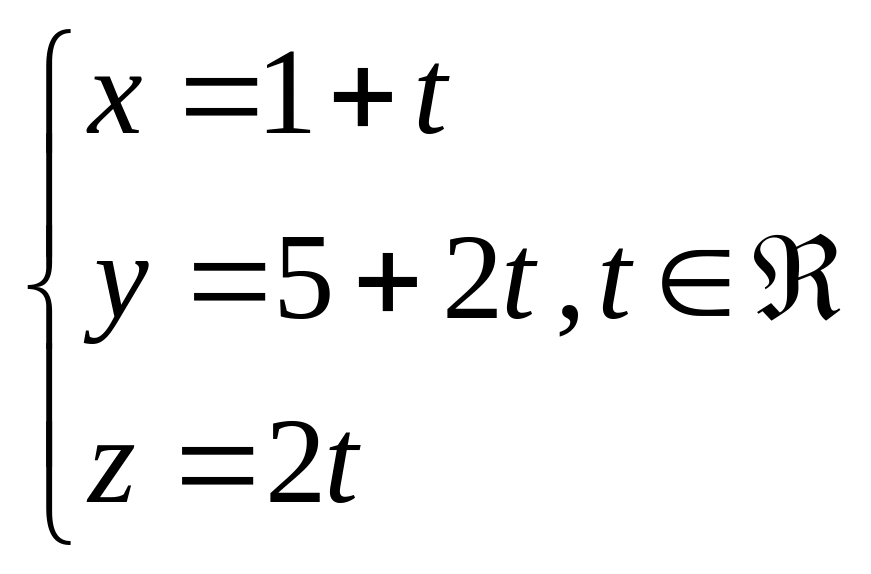
г) Найдем уравнение плоскости ВСS

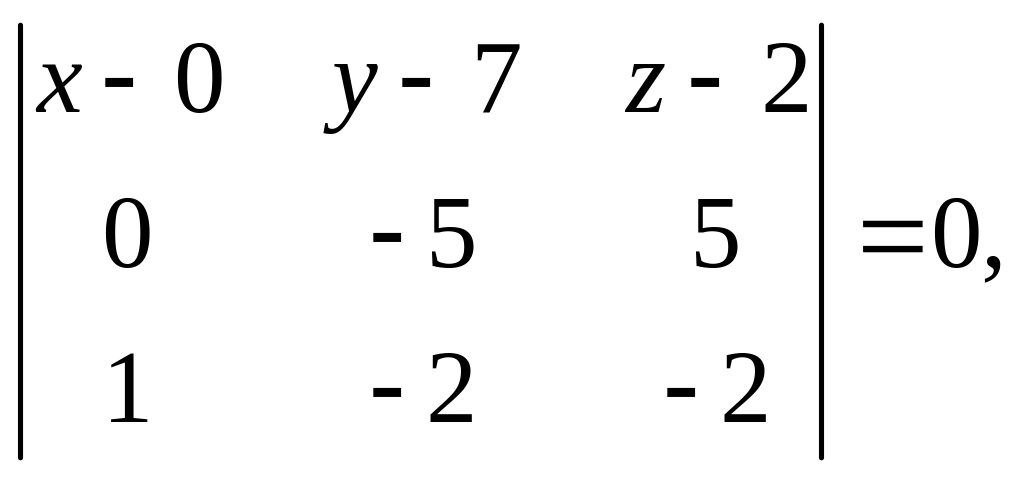
Косинус угла найдем по формуле

Отсюда

д) Объем пирамиды

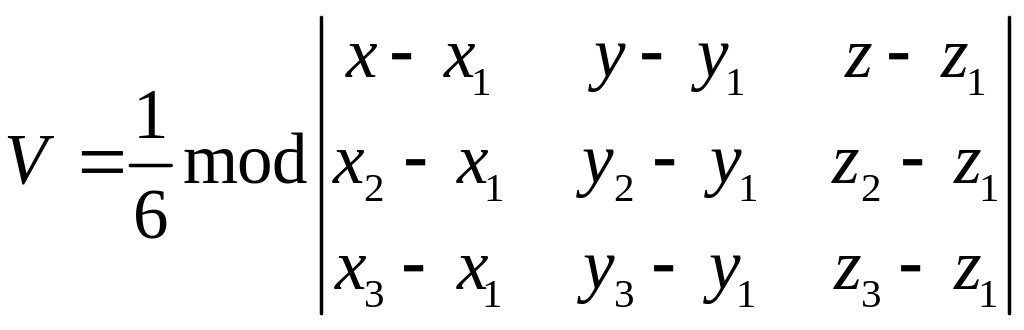
е) Т.к. прямая SД параллельна АВ, то направляющие векторы прямых совпадают Составим уравнение прямой SД, проходящий через точку S(1,5,0)

ж) Площадь грани вычислим по формуле

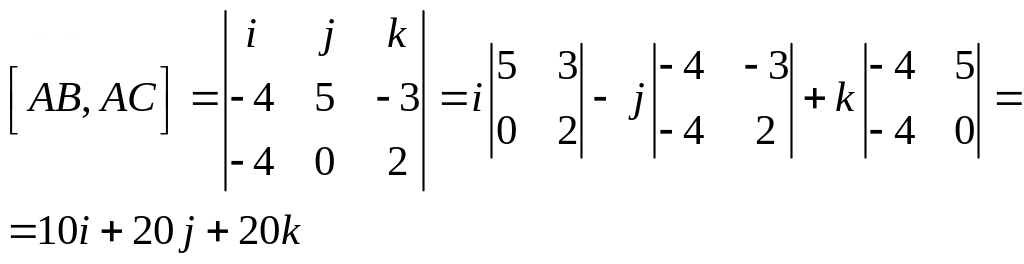
Задача 8. Методом параллельных сечений исследовать форму поверхности

Решение: Будем пересекать поверхность горизонтальными плоскостями .

Подставим в уравнение. Получим

Откуда видно, что любом таком сечении получаются окружности радиуса , наименьшая из которых имеет радиус равный 6(h=0). Сечение плоскостями x=с дает гиперболы

Сечение плоскостями , также дает гиперболы

Координатные плоскости являются плоскостями симметрии. Поверхность изображена на рисунке

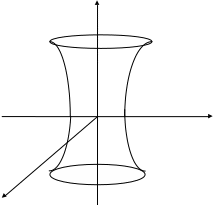
Задача 9: Найти предел функции не пользуясь правилом Лопиталя.

Решение:

а)

= =

б)

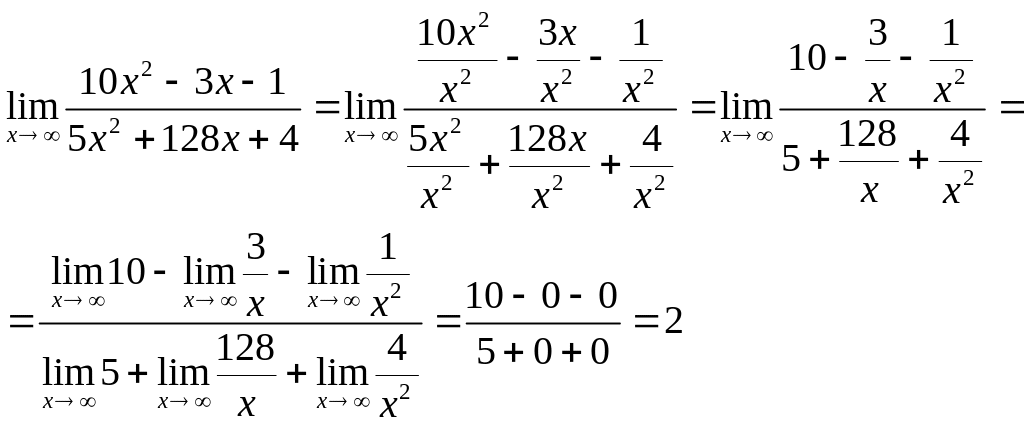
в)

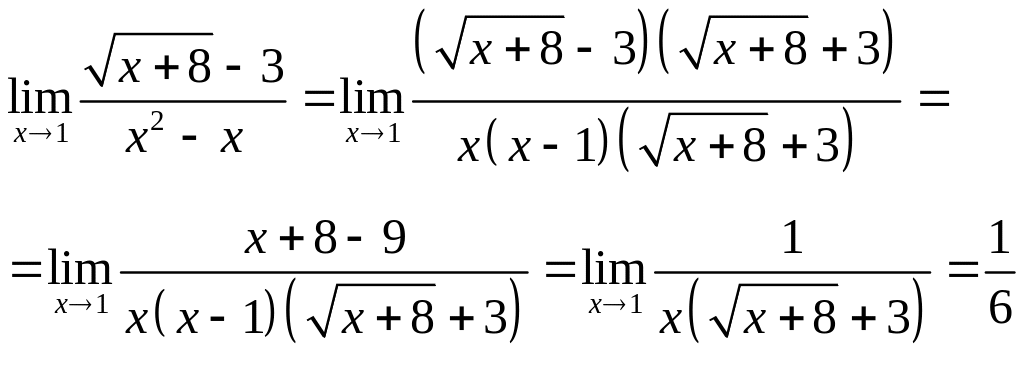
г)

д)

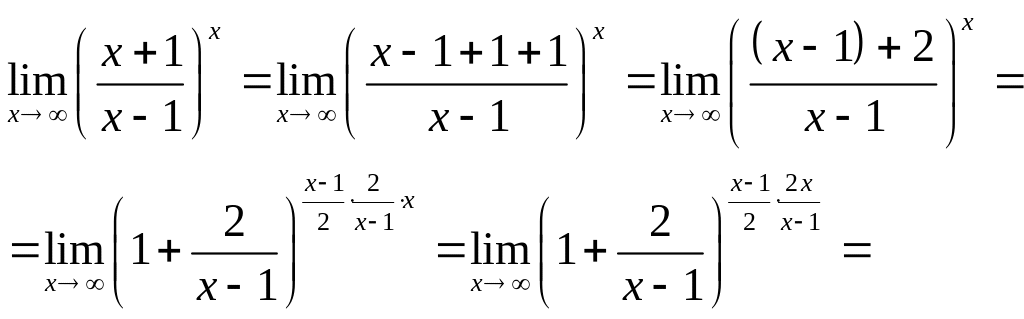
Задача 10. Найти производную заданной функции

а)

б)

в)

г)

Решение:

Применяя правила дифференцирования и используя таблицу производных, находим:

а)

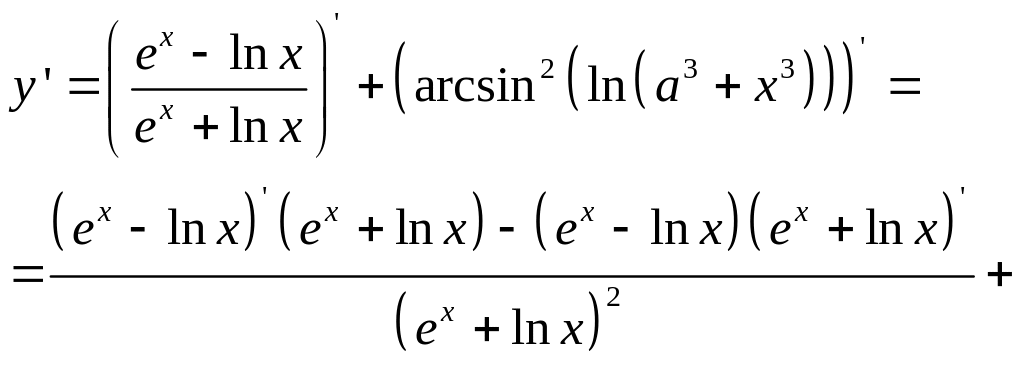
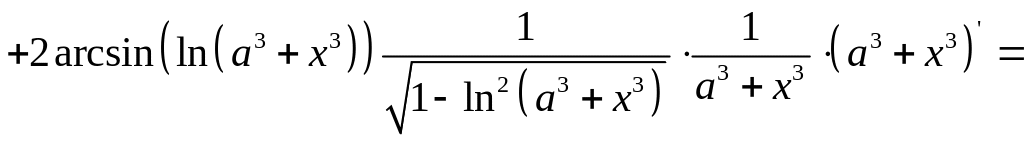
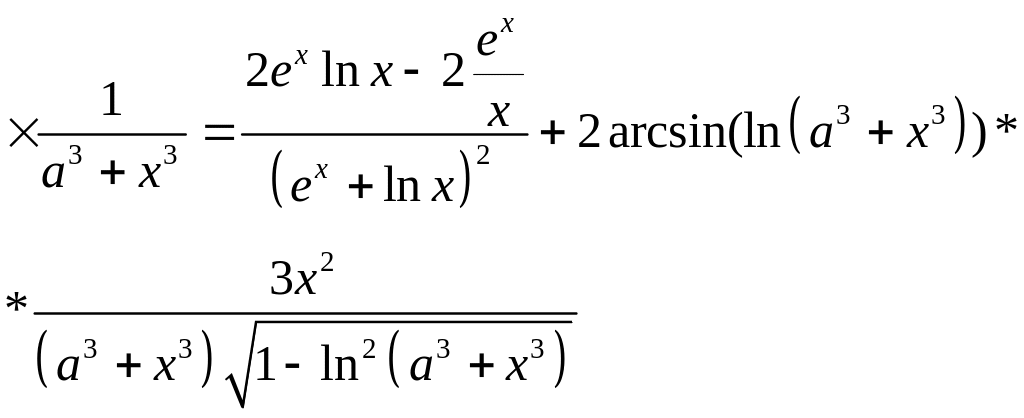
б)

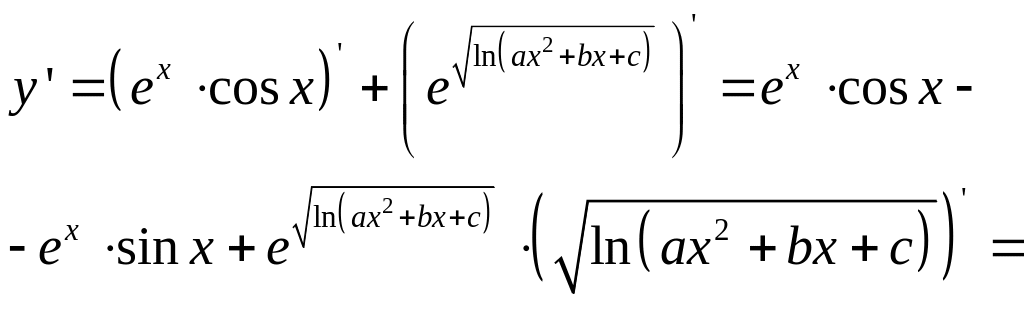
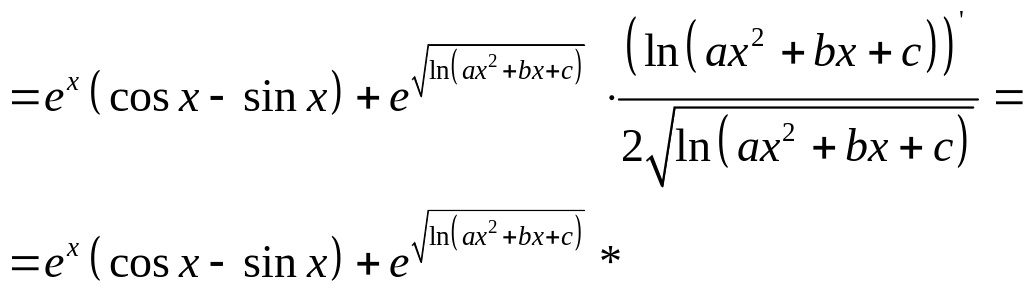
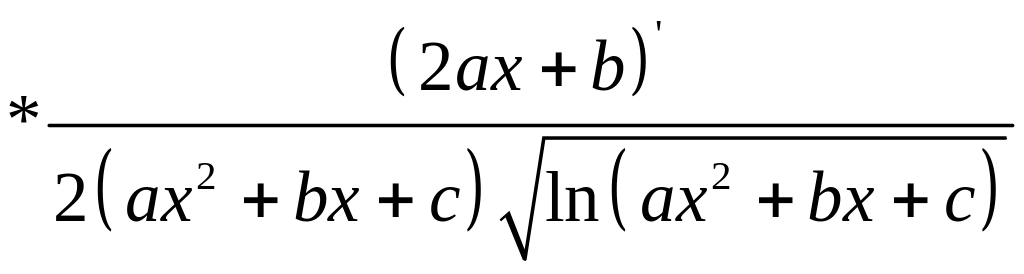
в)

Прологарифмируем обе части:

Продифференцируем обе части

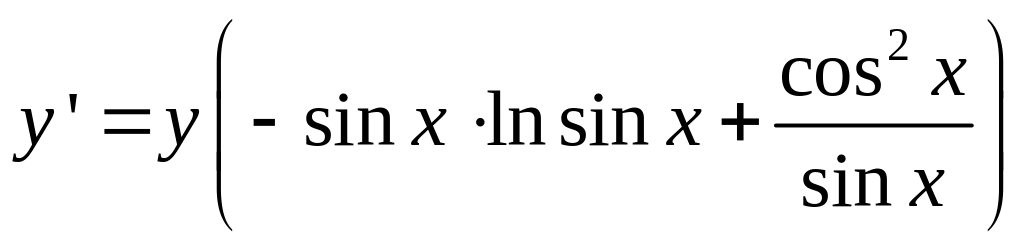
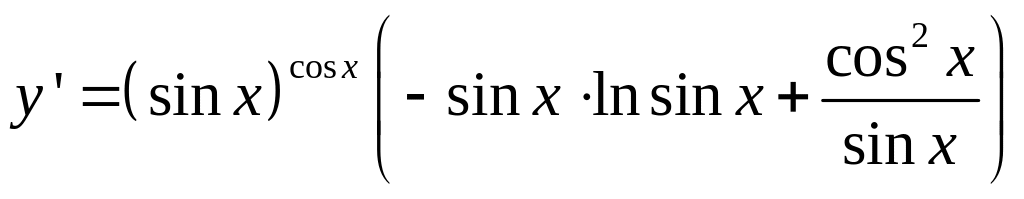
г) Дифференцируя обе части равенства, имеем

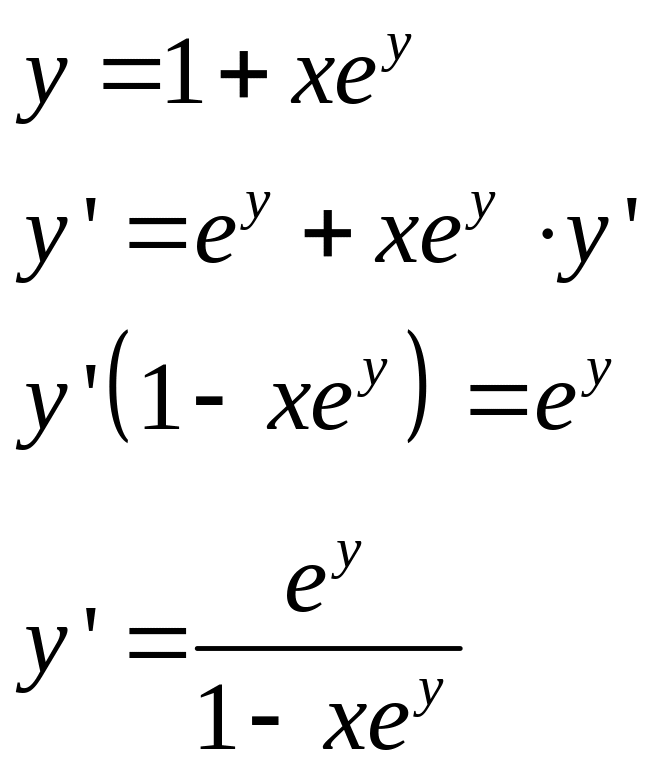
Т.к. по условию , то получаем

Задача 11. Дана функция в точке и

а) Установить является ли функция непрерывной в этих точках

б) Найти пределы слева и справа

в) Сделать схематический чертеж

Решение:

В точке x = 0 функция непрерывна, т.е.

В точке x = 2

предел слева

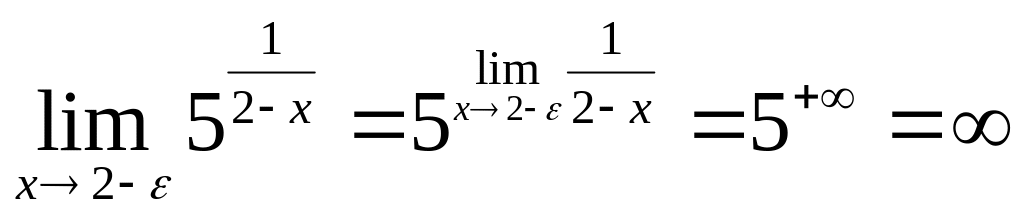
предел справа

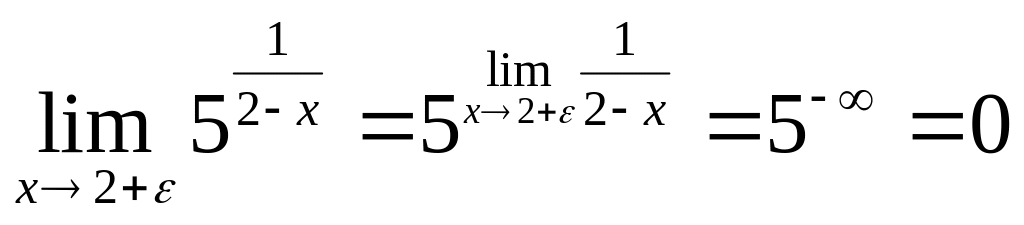
Схематичный чертеж на рис 1

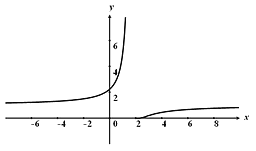
Рисунок 1

Задача 12.

x + 1, если x ≤ 0

Дана функция y = x², если 0 > x ≤ 2

½ x + 3 , если x ≥ 2

Найти точки разрыва, если они существуют сделать чертеж.

Решение:

График функции изображен на рисунке

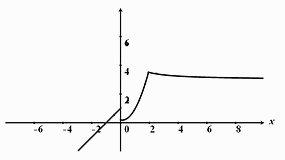
В точке x = 0 разрыв первого рода т.к.

В точке x = 2 разрыва нет.

В остальных точках функция непрерывна.

Задача 13.

a) С помощью преобразования графика функции построить функцию

Решение:

От функции к функции можно перейти с помощью следующей цепочки преобразований:

На рисунке изображены соответствующие графики:

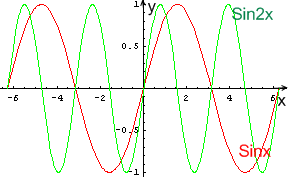
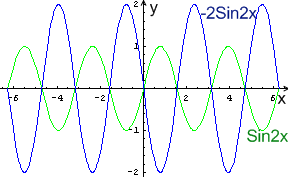
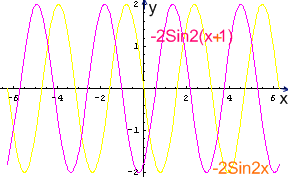
б) Построить по точкам график функции

Решение:

Рассмотрим два случая

1) x – 2 ≥ 0 x ≥ 2 тогда

2) x – 2 < 0 x < 2 тогда строим график

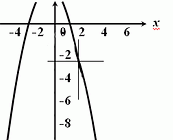
Задача 14. Используя правило Лопиталя вычислить пределы:

а)

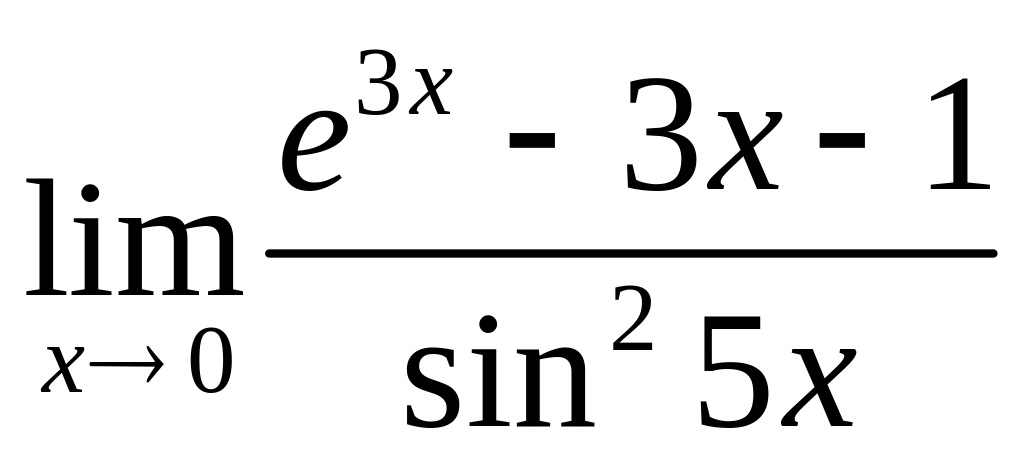
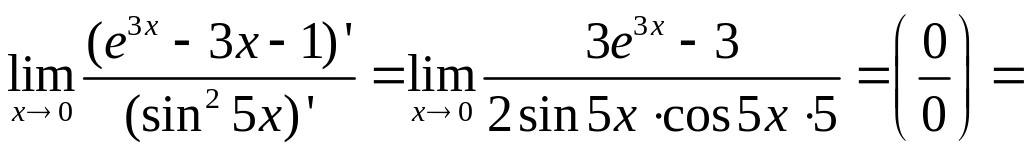
б)

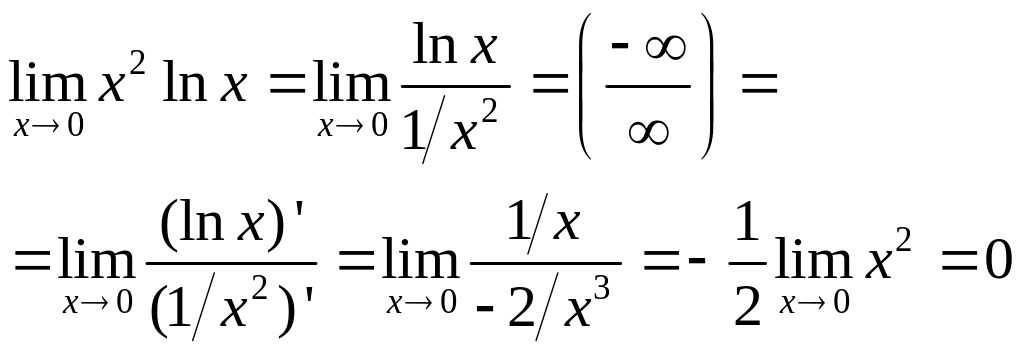
в)

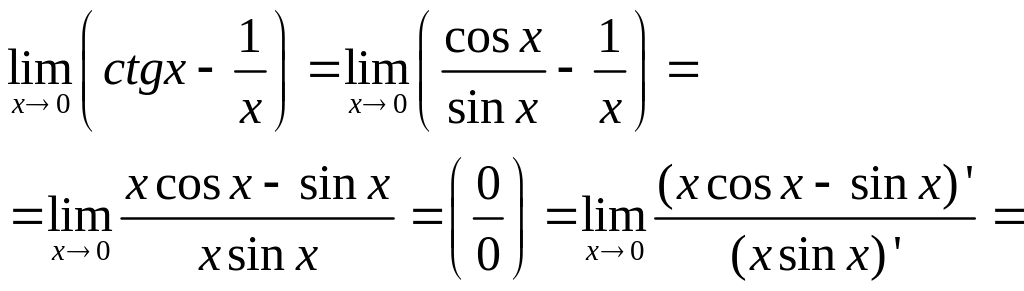
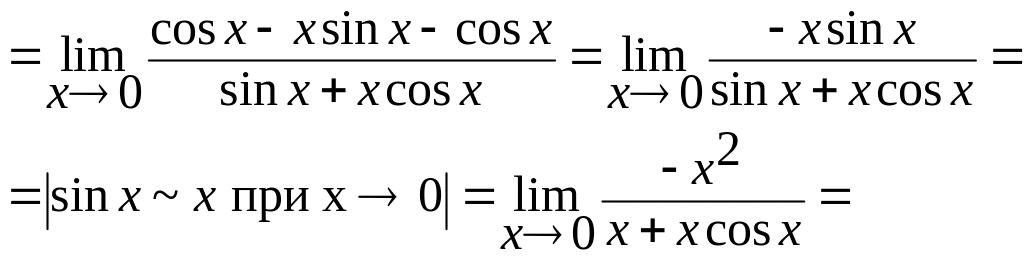
г)

Имеем неопределённость вида . Положим и прологарифмируем обе части равенства

Найдём

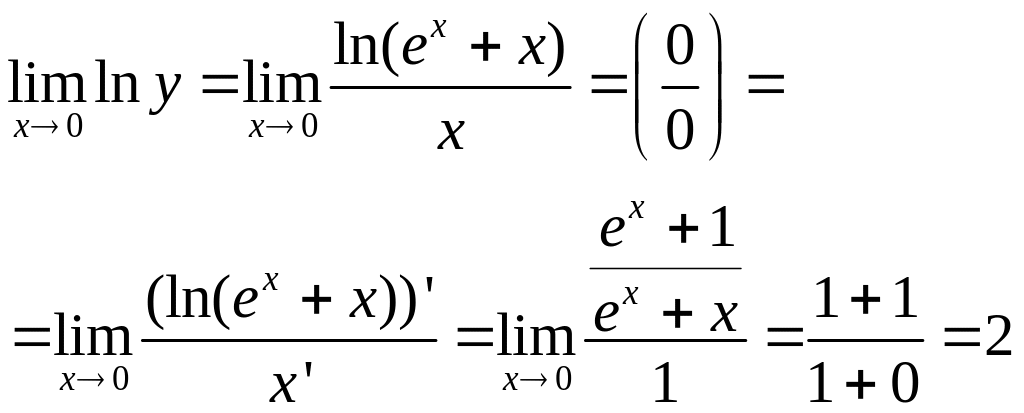
Поскольку , то

Задача 15. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить её график:

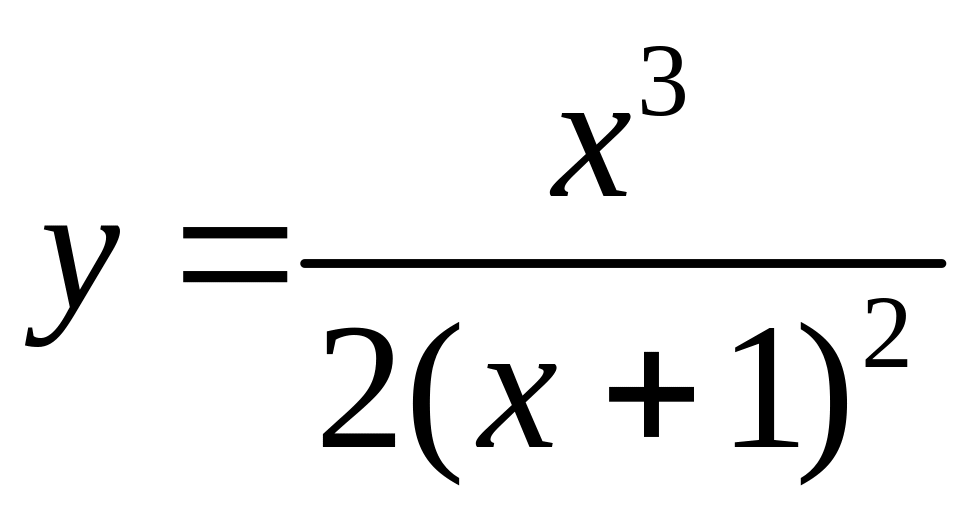
Решение: Приведём схему полного исследования функции

1. Область определения функции

2. Чётность, нечётность, переодичность

3. Точки разрыва функции; приделы при концам промежутков области определения; асимптоты

4. Интервалы возрастания и убывания функции, точки экстремума; вычислить значения экстремумов

5. Интервалы выпуклости и точки перегиба

6. Точки пересечения графика с осями координат

7. График

1. Функция определена, если , значит

2. Т.к. область определения функции не является симметричным множеством относительно начала координат, то функция не может быть чётной, нечётной и периодической.

3. Найдём пределы функций при концам промежутков области определения

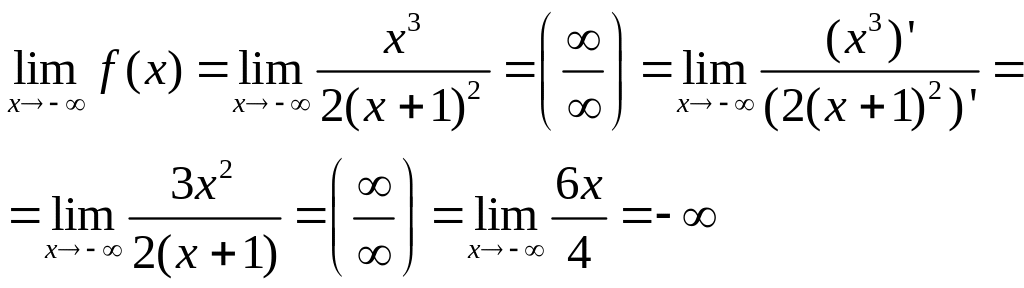
Аналогично, получаем что

Поскольку

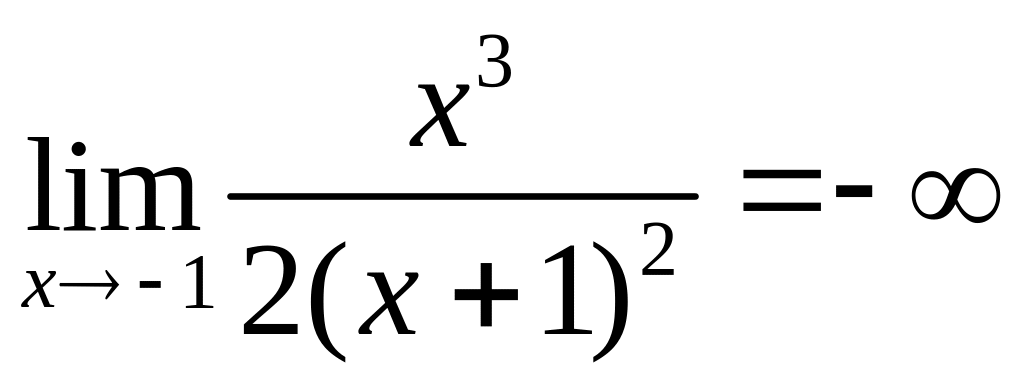, то точка - точка разрыва второго рода, а - вертикальная асимптота.

Найдём наклонные асимптоты , где

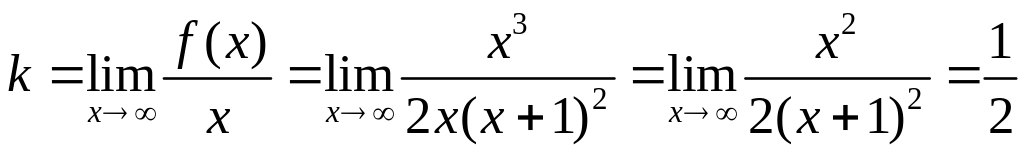
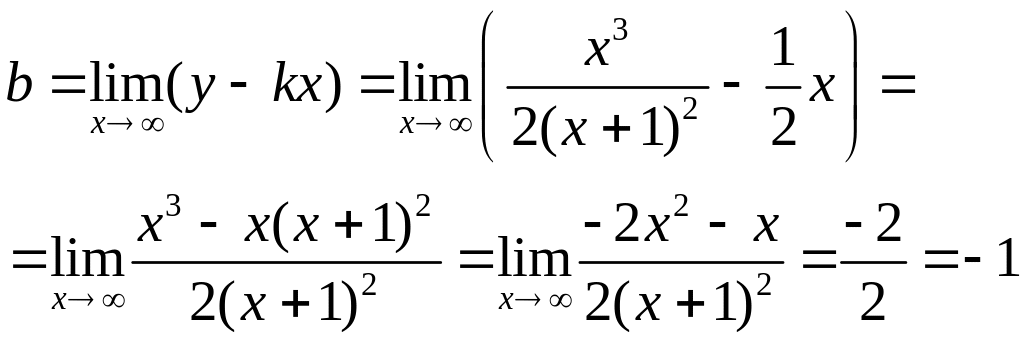
Следовательно, - уравнение наклонной асимптоты

4. Производная

определена на

Поскольку при , , то это критические точки функции. Так как

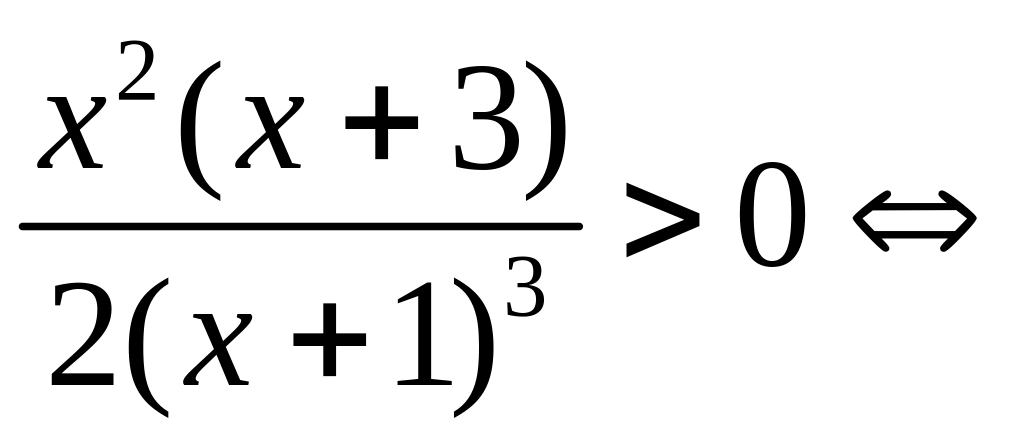
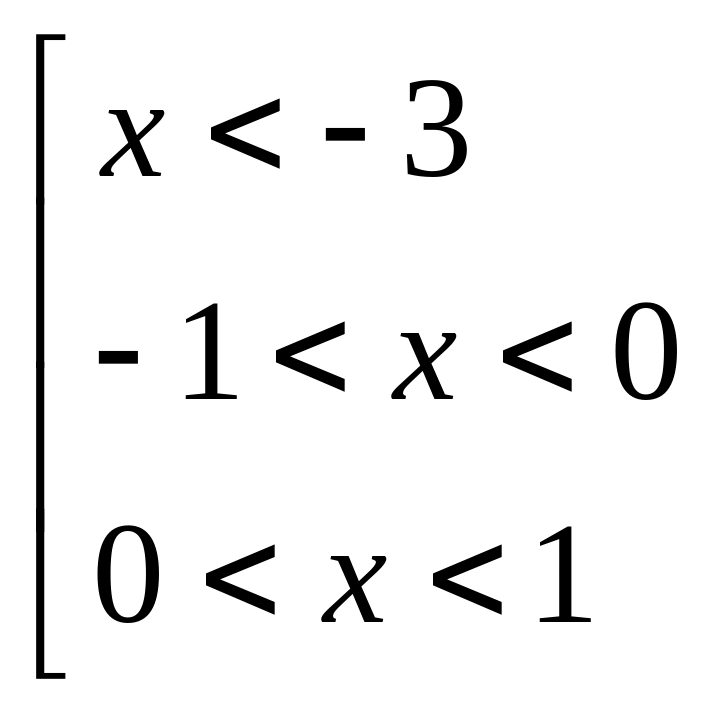
при

при

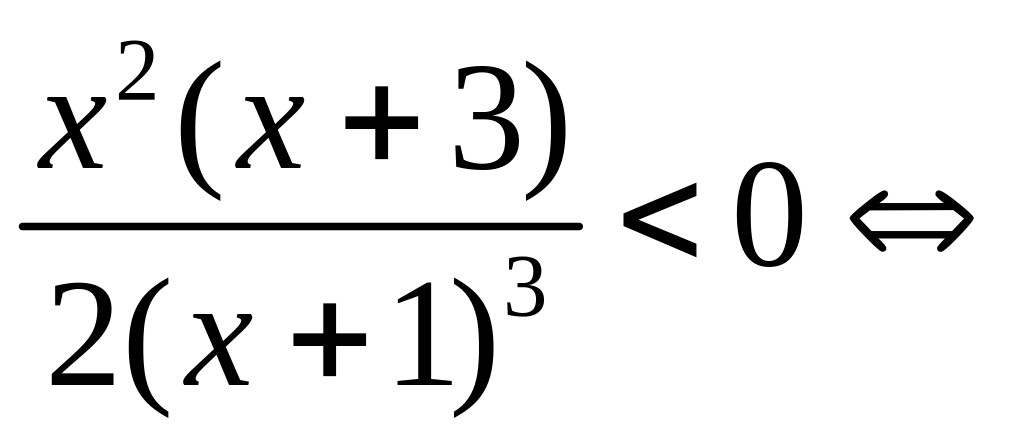
то на интервалах , функция возрастает, а на интервале

- убывает.

При функция имеет максимум, т.к. переходе через эту точку меняет знак с «+» на « ».

, значит точка 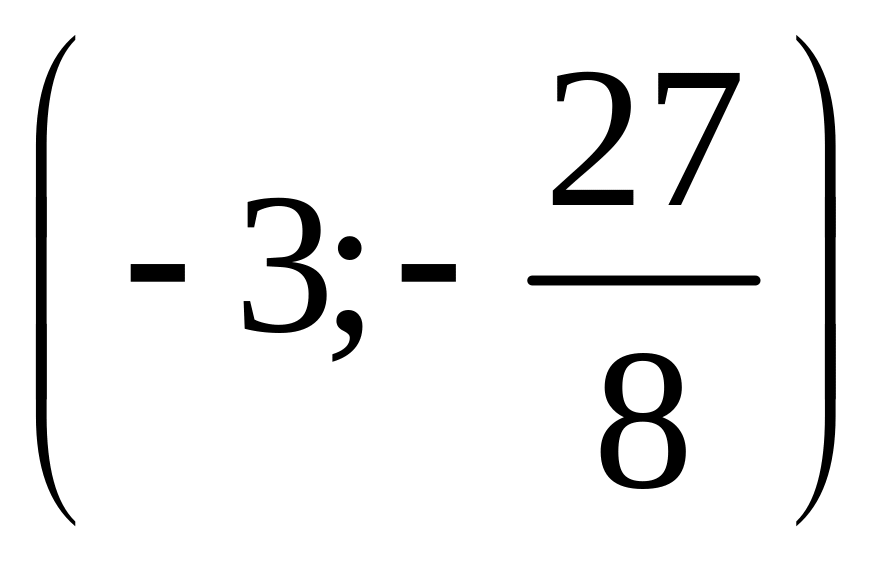- точка максимума.

5. Находим вторую производную

Она определена для . Поскольку при , то определив знак на каждом из интервалов , получим, что для

, график выпуклый; для график вогнутый.

При переходе через точку производная меняет знак, поэтому - точка перегиба, причём .

6. График функции пересекает координатные оси в т. .

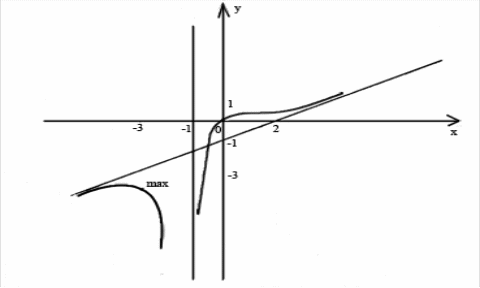
Задача 16. По формуле Тейлора с остаточным членом в форме Лагранжа у функции вычислить значение с точностью до при .

Решение: Формула Тейлора с остаточным членом в форме Лагранжа имеет вид

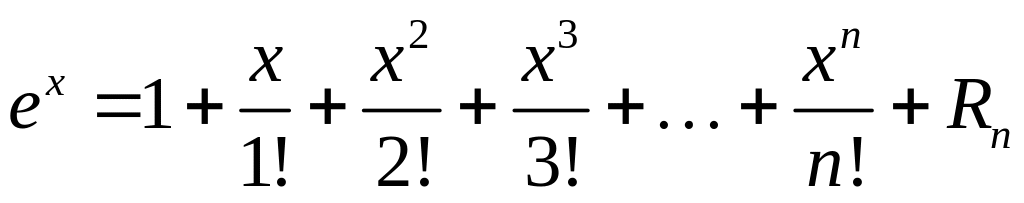
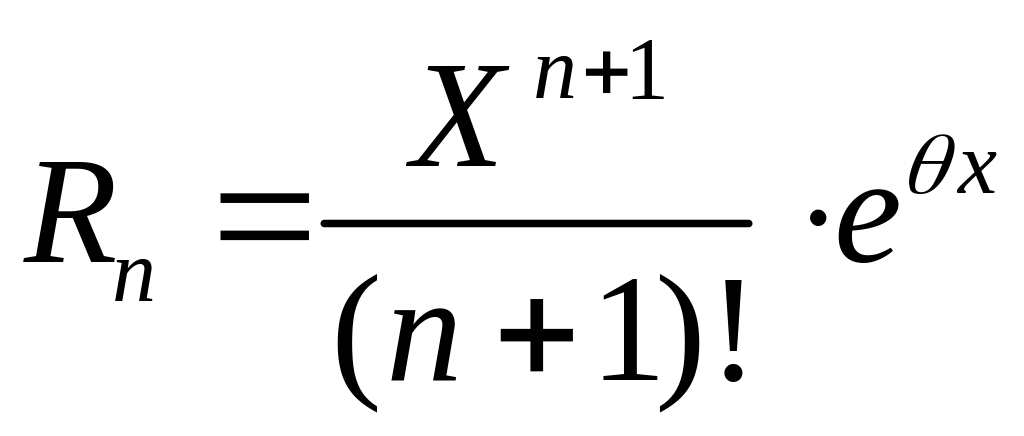отсюда получаем

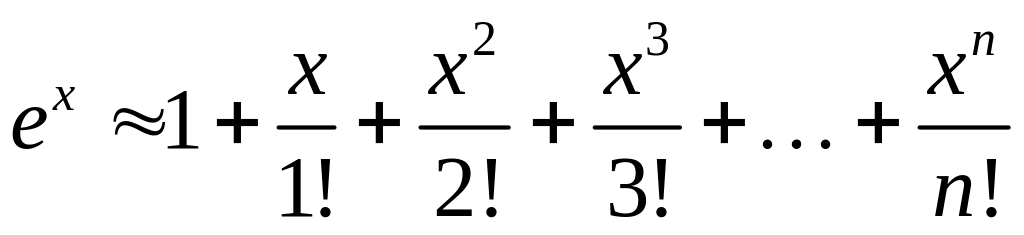
Для любого значения имеем отсюда или следовательно 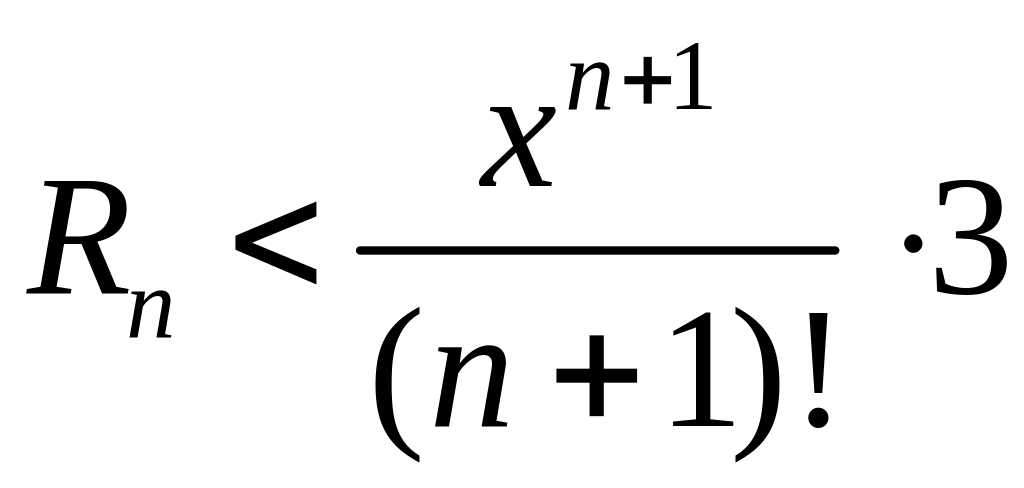следованием или

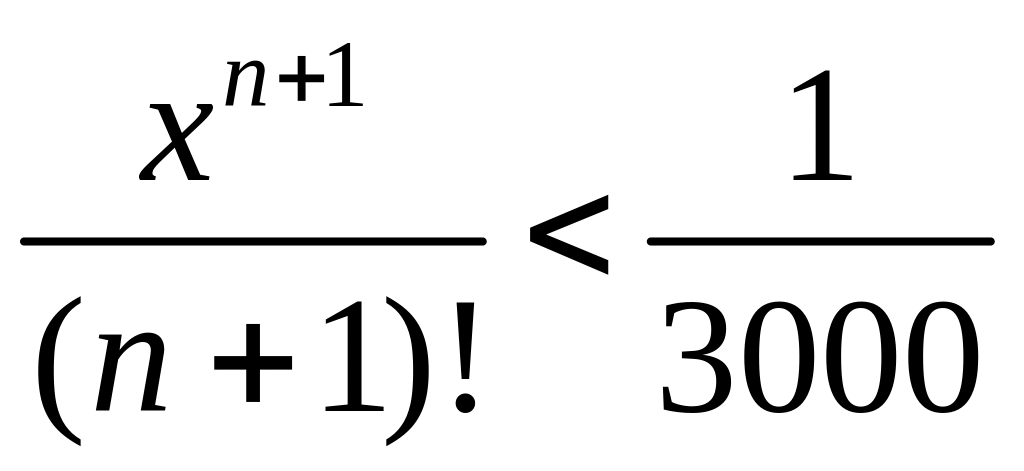
Следовательно, для заданной точности каждый отброшенный член должен быть меньше .

При эта точность достигается при , а при .

Ответ:

.

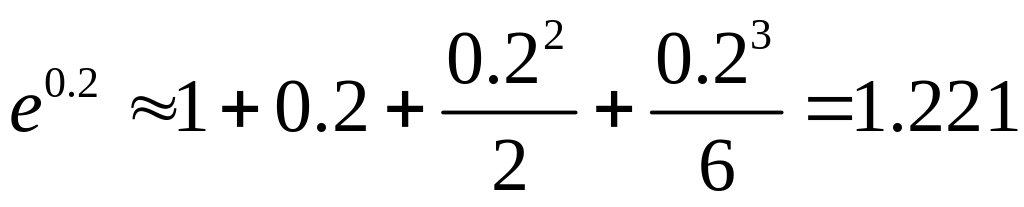Задача 17. Найти наибольшее и наименьшее значения функции на отрезке

Решение: Функция определена на

Производная определена на и обращается в нуль при . Эти точки принадлежат отрезку .

Тогда

Ответ: , .

Задача 18. Разложить число 100 на два слагаемых так, чтобы их произведение было наибольшим.

Решение. Пусть - первое слагаемое, будет второе слагаемое.

Произведение этих слагаемых даёт функцию .

По условию задачи . Найдём экстремумы этой функции , ,

то при функция достигает максимума.

следовательно функция принимает наибольшее значение в критической точке .

Ответ: Произведение двух слагаемых будет наибольшее, если они равны 50.

Задача 19. Отделить действительные корни уравнения

Применяя комбинированный метод вычислить их с точностью до шести десятичных знаков.

Решение: - непрерывная функция на всей области определения в точке x=0 , а в точке x=-1 y(-1)=-4. Следовательно на отрезке [-1;0] функция обращается в ноль и уравнение на этом отрезке имеет корень. Найдем . Так как для всех , то функция y(x) монотонно возрастает на всей области определения и имеет только единственный корень на отрезке [-1;0]. Уточним отрезок на котором находится корень. Разделим отрезок [-1;0] на десять частей и убедимся, что функция y(x) меняет знак только на отрезке [-0.7;-0.6]. Следовательно корень уравнения лежит на отрезке [-0.7;-0.6]. Заметим что чем точнее отделен корень, тем меньше шагов методом хорд и методом касательных надо выполнить. Проверим, для какой из этих двух точек выполняется условие поскольку , то применяя метод Ньютона положим . Находим .

.

По методу хорд положим получим

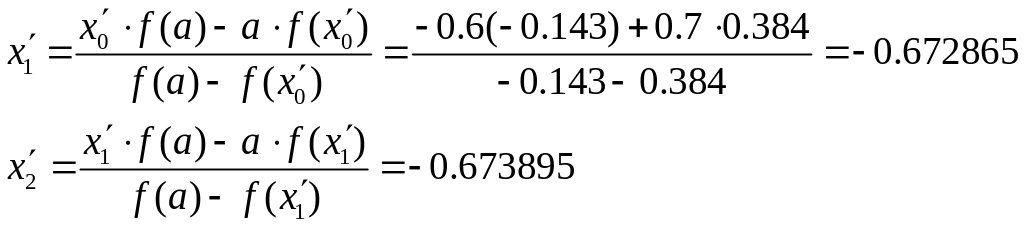
Следовательно корень данного уравнения находится на отрезке [-0.673593;-0.673585]. Данной точности еще недостаточно. Положим теперь a=-0,673593, найдем . .

Таким образам x=-0.673593 корень данного уравнения. Заметим, чем точнее отделен корень первоначально, тем меньше шагов методом хорд и касательных надо выполнить.