Лабораторная работа № 9

Вынужденные электрические колебания

Цель работы: изучение колебательных процессов на примере вынужденных

электрических колебаний.

Приборы: генератор низкочастотный «ГЗ-56/1», вольтметр «ВЗ-38», магазин

емкостей «Р-544», магазин сопротивлений «МСР-60М», набор

индуктивностей, сервисный осциллограф «ЕО-213».

Вставить фотографию

КРАТКАЯ ТЕОРИЯ

Среди различных видов движений в физических системах важное значение имеют периодические колебания.

Под колебаниями понимают всякий периодический или почти периодический процесс, в котором значения той или иной физической величины повторяются точно или приближенно через равные или почти равные промежутки времени.

К очень распространённому типу колебательных движений относят так называемые малые колебания, которые система совершает вблизи положения устойчивого равновесия. В настоящей работе мы будем рассматривать малые вынужденные колебания в последовательном колебательном контуре. Так называемая система, состоящая из последовательно соединённых катушек индуктивности , омического сопротивления (под понимается сопротивление катушки и внутреннее сопротивление источника) и конденсатора (рис. 1).

Закономерности, которые наблюдаются при вынужденных колебаниях в таком простом электрическом контуре, являются общими для колебаний различной природы (механических, электромагнитных, в том числе световых, акустических и др.). К числу этих закономерностей относится явление резонанса, сдвиг фаз между вынуждающей силой и вынужденными колебаниями, все особенности амплитудно-частотной и фазочастотной характеристик, в частности, поведение при малой и большой частоте, зависимость формы характеристик от уровня потерь системы. Хорошо изучив электрические колебания, можно с успехом анализировать путём аналогий колебательные процессы в любых других колебательных системах.

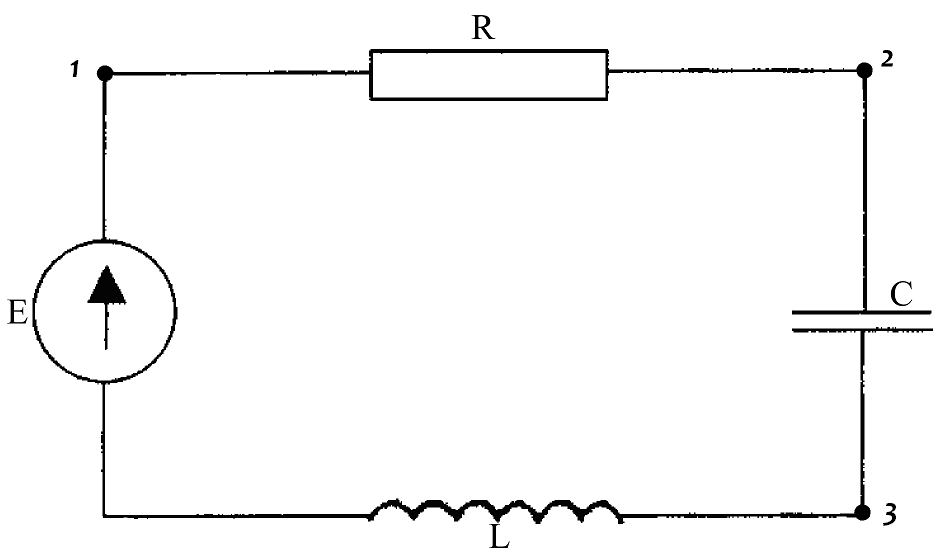
Рис. 1 Схема последовательного колебательного контура с

внешним источником ЭДС.

Применим к замкнутому контуру, схема которого представлена на рис. 1, уравнение Максвелла

,

Оно может быть переписано в следующем виде:

, (1)

где - падения напряжения соответственно на омическом сопротивлении и на конденсаторе в любой момент времени, — внешняя ЭДС, - ЭДС самоиндукции, возникающая на зажимах катушки вследствие изменения во времени силы тока, проходящую через последнюю. Сопротивление провода катушки считается здесь пренебрежительно малым. По закону Ома, падение напряжения на омическом сопротивлении составляет величину

, (2)

где - ток в цепи, - плотность тока, - удельное сопротивление.

Падение напряжения на конденсаторе равно

. (3)

где - электрический заряд обкладок конденсатора в данный момент времени. Перемещение носителей тока в проводах, соединяющих элементы цепи, и в других элементах цепи приводит к накоплению или расходованию этого заряда:

(4)

ЭДС самоиндукции катушки пропорциональна скорости убывания тока:

(5)

Воспользовавшись формулами (2) и (5), приведем выражение(1) к виду:

(6)

Самостоятельный интерес представляют вынужденные колебания под действием внешней силы, меняющейся по синусоидальному закону. Положив , приведем (6) к виду

(7)

Здесь использованы общепринятые обозначения: - коэффициент

затухания, - собственная частота колебательного контура в отсутствие затухания. В случае малых колебаний ток в контуре достаточно мал, так что катушка не деформируется ( ). Будем считать, что аналогичные предположения выполнены и для других элементов цепи. Тогда уравнение (7) есть линейное неоднородное уравнение с постоянными коэффициентами. Рассмотрим более важный случай, когда потери в колебательной системе относительно малы: . Решение уравнения (7) запишем в виде:

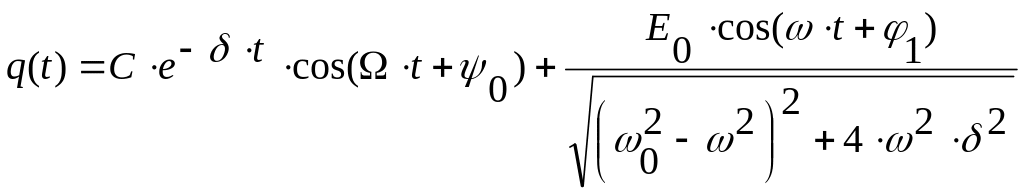, (8)

где .

Так как - ограниченная функция, по истечении достаточно большого, но конечного промежутка времени, благодаря экспоненциальному множителю , первым слагаемым можно пренебречь (собственные колебания в контуре станут пренебрежимо малыми), и выражение (8) примет вид:

, (9)

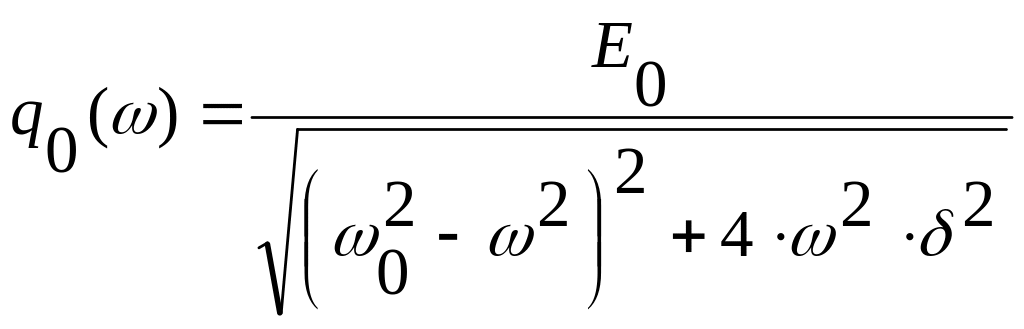где , (10)

Заметим, что сдвиг фаз между вынуждающей силой и зарядом зависит от частоты . Под действием периодической ЭДС, в установившемся режиме, величина заряда на конденсаторе совершает колебания с частотой равной частоте вынуждающей силы, и амплитудой , зависящей от частоты последней. Такие колебания называют вынужденными. Рассмотрим колебания тока в контуре и колебания напряжений . Для физических величин удобно применять соответствующие им комплексные :

(11)

Так как , то: . Таким образом, получим следующее выражение для силы тока:

(12)

Воспользовавшись формулами (2) – (4), найдем, что:

(13)

(14)

(15)

Как видно из этих соотношений, напряжение на омическом сопротивлении совпадает по фазе с током в цепи, в то время как напряжение на катушке опережает, а напряжение на конденсаторе отстает по фазе от тока в цепи контура на величину . Исследуем характер зависимости амплитуды колебаний заряда от частоты, записав эту зависимость в явном виде:

, где (15)

Величина представляет собой установившийся (частота =0) заряд на конденсаторе в случае, когда . При возрастании частоты от 0 до амплитуда сначала возрастает, а затем проходит через максимум и асимптотически убывает к нулю (рис.2). Приравняв к нулю первую производную , получим, что амплитуда имеет максимальное значение при . При это значение незначительно отличается от , поэтому за максимум амплитуды можно принять ее значение при

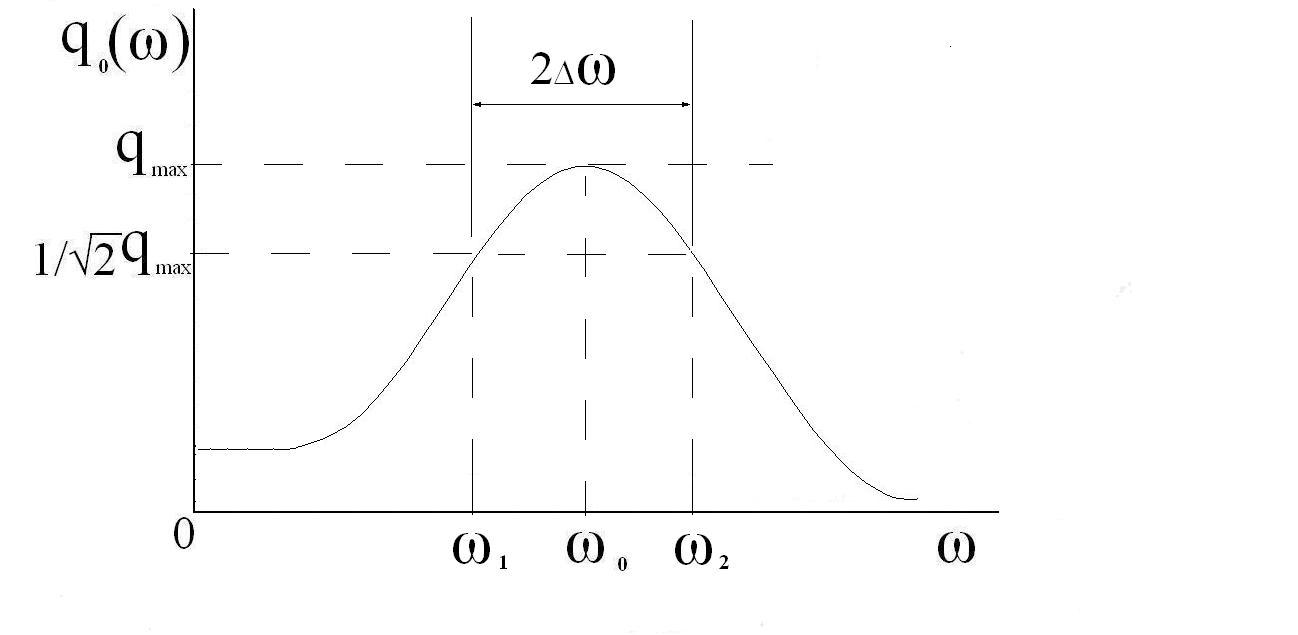
Рис. 2 Амплитудная резонансная кривая колебания заряда на конденсаторе.

Явление возбуждения сильных колебаний при частоте внешнего возбуждающего силы близкой к собственной частоте колебательной системы, называют резонансом. Кривая, изображающая зависимость амплитуды колебаний от частоты внешней силы, называется амплитудной резонансной кривой.

При установившихся вынужденных колебаниях в контуре энергия, запасенная в контуре, остается неизменной. В то же время контур непрерывно поглощает энергию от источника ЭДС, которая рассеивается на омическом сопротивлении. Обозначим через среднее по большему промежутку времени или за период колебаний количество энергии, поглощаемой контуром. Эта величина равна средней мощности, развиваемой источником ЭДС, и зависит от частоты внешней силы:

После выполнения несложной процедуры интегрирования, окончательно получим:

(16)

Используя элементарное тригонометрическое тождество и полученное выше выражение для , получим

.

Подставляя это выражение и явный вид из (10) в формулу (16), приходим к иному выражению для :

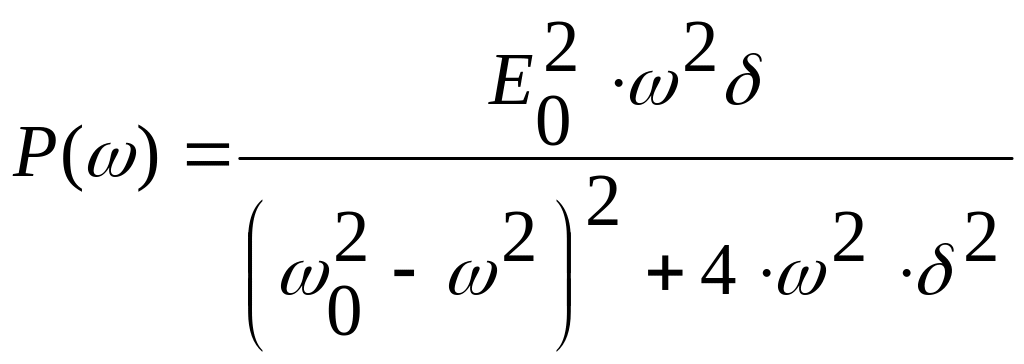(17)

Такой вид зависимости поглощения от частоты называется дисперсионным.

При условии средняя мощность, развиваемая источником, достигает максимума в момент резонанса, т. е. в данном случае при и равна

.

Рассмотрим область вблизи резонанса. Максимум амплитуды при дается выражением

(18)

Отношение максимального значения к статическому отклонению называется добротностью контура. Обозначается добротность через . Имеем:

(19)

Для свободных затухающих колебаний (при ), согласно (8), имеем

Величина называется логарифмическим декрементом затухания. За один период колебания заряда его амплитуда уменьшается в раз, а энергия, запасенная в конденсаторе колебательного контура уменьшается в раз. Отсюда видно, что добротность характеризует способность колебательной системы рассеивать энергию. Чем выше добротность тем меньше энергия рассеивается колебательной системой. Заметим, что часто понятие добротности колебательной системы вводится иначе, но смысл его всегда один и тот же - мера скорости диссипации энергии, запасенной в колебательной системе.

Кроме максимальной амплитуды, резонансная кривая характеризуется шириной. Пусть и - значение частоты , при которых энергия колебания вдвое меньше энергии колебаний в максимуме (рис.2). Тогда

,

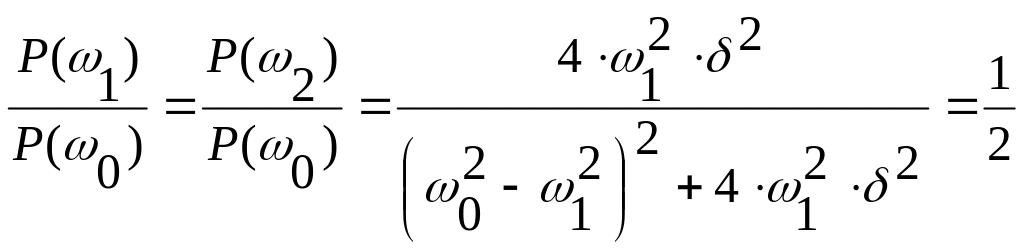откуда получим

и аналогично .

Если и , то:

. (20)

Причем согласно (19) .

Сделанное приближение справедливо при , т. е. при .

Величина называется шириной резонансной кривой. Из (13), (14) и (19) получаем

при (21)

Таким образом, чем больше добротность контура, тем выше резонансная кривая, т. е. максимум становится более острым (рис.3).

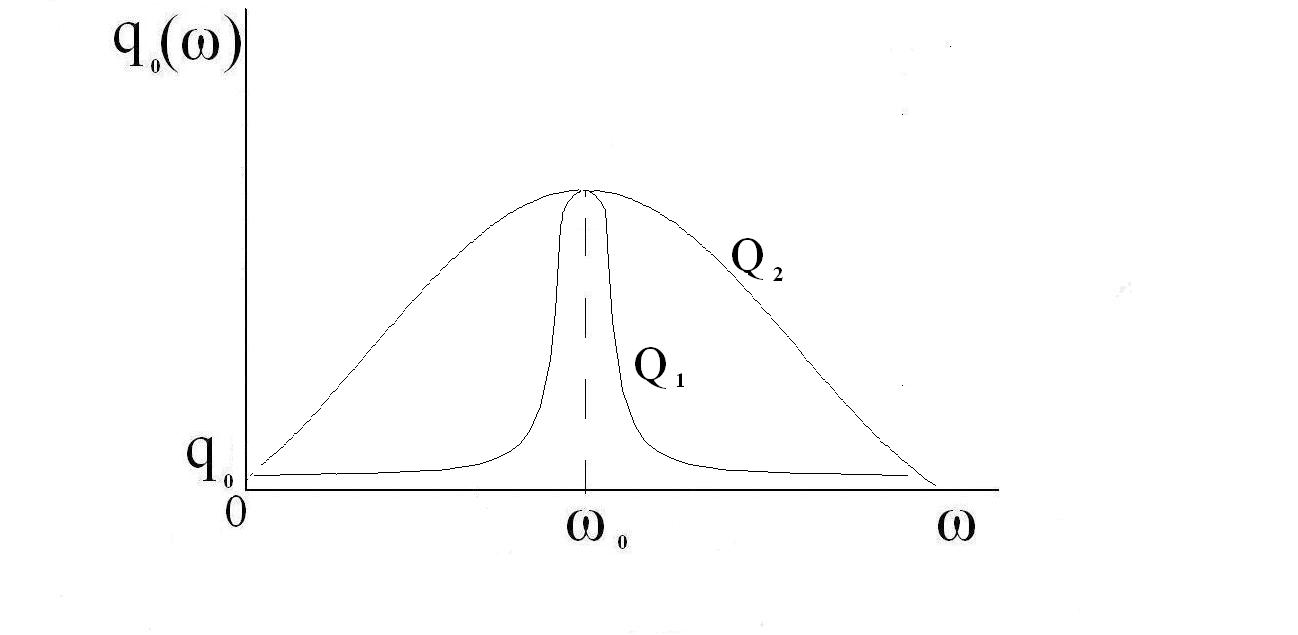
Рис. 3 Резонансные кривые колебательного контура в случае различных величин добротности ( )

Отметим характерную особенность хода изменения разности фаз между колебаниями и вынуждающей силой при изменении частоты последней. Колебание всегда запаздывают относительно внешней силы. Запишем явный вид функциональной зависимости :

(22)

Из (22) видно, что при и при . Изменение от 0 до происходит в узкой ( ) области частот, близких к . Через значение разности фаз проходит при . На рис.4 приведены кривые зависимости разности фаз от частоты при различных добротностях. Кривая называется фазовой резонансной характеристикой.

Рис. 4 Фазовые резонансные характеристики колебательных контуров с различными добротностями ( )

В заключение сформулируем условие квазистационарности, выполнение которого предполагалось при рассмотрении вынужденных колебаний в колебательном контуре. Квазистационарность означает, что мгновенное значение тока практически одинаковы на всех проводов, входящих в цепь контура (в том числе и провода, из которого состоит катушка). Для этого изменения тока во времени должны происходить достаточно медленно по отношению к времени распространения электродинамических взаимодействий (со скоростью света) в контуре так, чтобы скорость распространения последних можно было бы считать мгновенной: характерное время изменения тока - период колебания : время распространения электродинамических взаимодействий , где - общая длина всех проводников контура. Условие квазистационарности будет выполнено, если , или .