Электронные оболочки атомов Электронные оболочки атома водорода.
Ранее мы рассмотрели
электрон в
-
состоянии, т.е. при
![]()
![]() и
и
![]() .
Это состояние атома водорода называется
основным.
.
Это состояние атома водорода называется
основным.
При
![]() и более атом водорода переходит в
возбужденное
состояние.
Возбужденные состояния с
и более атом водорода переходит в
возбужденное
состояние.
Возбужденные состояния с
![]() различаются квантовыми числами
и
.
различаются квантовыми числами
и
.
Условная схема состояний

Уровни, имеющие одинаковую энергию, образуют электронную оболочку (1-я оболочка содержит только 1 уровень, 2-я – 4 уровня, 3-я – 9 уровней):
![]() -
оболочка,
-
оболочка,
![]() -
-
![]() -
оболочка,
-
оболочка,
-
![]() -
оболочкой и т.д.
-
оболочкой и т.д.
При наложении внешних электрических или магнитных полей разные уровни оболочек расщепляются (т.е. приобретают разные поправки энергий).
Испускание и поглощение света происходит при переходе электрона с одного энергетического уровня на другой. Реализуются лишь такие переходы, при которых выполняется так называемое правило отбора:
![]() .
.
Это означает, что
возможны только переходы, при которых
орбитальное квантовое число
меняется на единицу (т.е. электрон из
-
состояния может перейти только в
-
состояние и т.д.). Существование правила
отбора связано с наличием момента
импульса у испускаемого фотона, которое
характеризуется квантовым числом
![]() ,.
При излучении или поглощении фотона
момент импульса атома меняется на
,.
При излучении или поглощении фотона
момент импульса атома меняется на
![]() .
Из закона сохранения момента импульса
атома следует, что должно выполняться
условие
.
.
Из закона сохранения момента импульса
атома следует, что должно выполняться
условие
.
Волновые функции возбужденных состояний.
Уравнение Шредингера для возбужденных состояний ( ) остается прежним: Решение его можно найти в виде
![]() =
=
![]() .
.
Для - состояния атома водорода ( , ) уравнение Шредингера имеет вид:
![]() .
.
Решение его:
 ,
где
,
где
![]()
(![]() -
совпадает с радиусом первой боровской
орбиты).
-
совпадает с радиусом первой боровской
орбиты).
Это решение можно получить, подставив и в общее решение радиального уравнения
![]() =
= ,
,
где
![]() -
полином Лагерра, имеющий (
-
полином Лагерра, имеющий (![]() )
корней.
)
корней.
Зависимости
![]() и
и
![]() для
-
состояния
для
-
состояния

Функция имеет узел - совокупность точек в пространстве, где ее амплитуда обращается в нуль.
Максимум функции
приходится на
![]()
Для
![]() -
состояния (
,
)
полином Лагерра не имеет корней (
-
состояния (
,
)
полином Лагерра не имеет корней (![]() ),
поэтому получаем
),
поэтому получаем
 .
.
Максимум
этой функции приходится на
![]() .
.
Плотность вероятности для - состояния
=![]() .
.
Максимальная
вероятность обнаружения электрона в
-
состоянии приходится на
![]() .
.
Функции
![]() для
-состояний,
-,
для
-состояний,
-,
![]() -
и
-
и
![]() -
состояний
-
состояний

С боровским радиусом
совпадают
![]() ,
соответствующие состояниям с максимальным
,
соответствующие состояниям с максимальным
![]() при данном
,
т.е. состояниям
(
при данном
,
т.е. состояниям
(![]() ),
(
),
(![]() ),
),
![]() (
(![]() )
и т.д.
)
и т.д.
Плотность вероятности локализации электрона в некоторой точке пространства равна
![]() ,
,
но,
![]() ,
то плотность вероятности не зависит от
,
то плотность вероятности не зависит от
![]() ,
а зависит лишь от
,
а зависит лишь от
![]() и
и
![]() .
.
Т .к.
.к.
![]() (
)
также не зависит от
,
то график зависимости
(
)
также не зависит от
,
то график зависимости
![]() обладает вращательной симметрией
относительно оси
.
обладает вращательной симметрией
относительно оси
.
Для
-
состояния (
,
![]() )
)
полином Лежандра
![]() ,
а
,
а
![]() ,
,
в этом случае
![]() .
.
В - состоянии ( ) при
полином Лежандра имеет вид
![]() ,
а
,
а
![]() и
и
![]() .
.
Максимальная
плотность вероятности – при
![]() ,
,
минимальная
– при
![]() .
.
При
![]()
![]()
и
![]() .
.
Максимум этой функции приходится на ,
минимум - при .
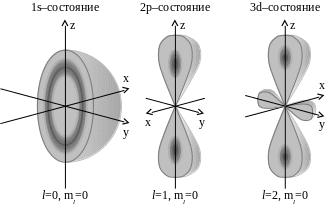
Распределение
полной плотности вероятности, определяемой
угловой плотностью вероятности, которая,
воздействуя на радиальную плотность
вероятности, модулирует ее (для
-
,
-
и
![]() -
состояний), имеет вид:
-
состояний), имеет вид: