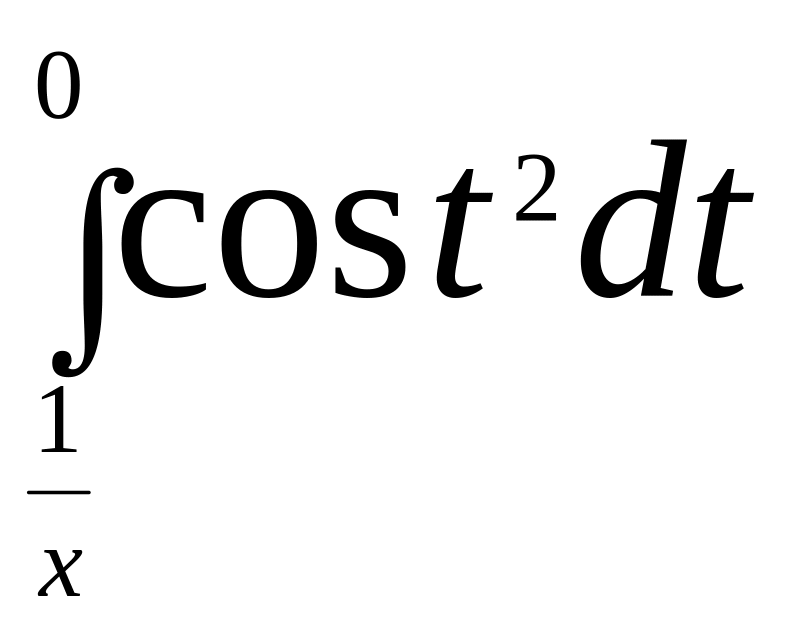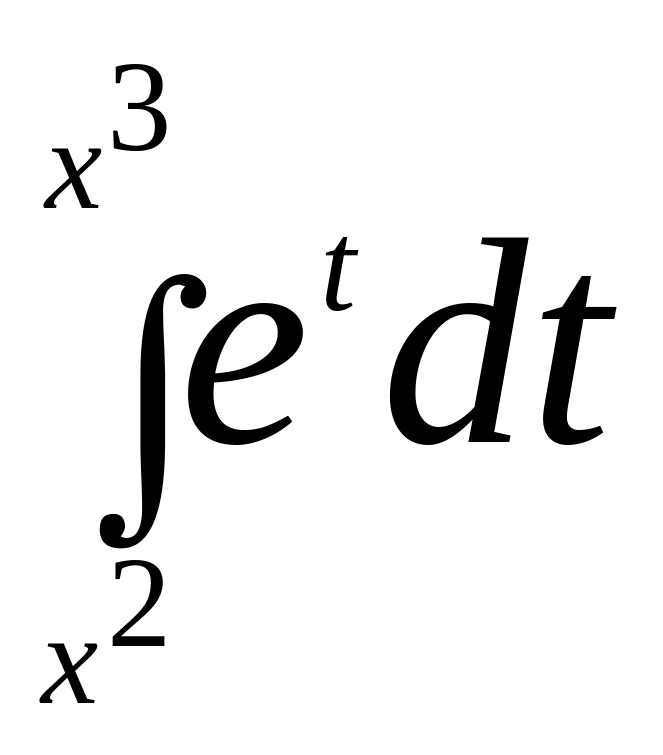Примеры для самостоятельного решения.
Найти интегралы:
17)![]() ;
18)
;
18) ![]() ;
19)
;
19) ![]() ;
20)
;
20)![]() ;
;
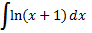 ;
22)
;
22) 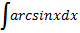 ;
23)
;
23) 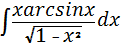 ;
24)
;
24)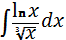 ;
;
25) 26)
26) ![]() ;
27)
;
27) ![]() ;
28)
;
28) ![]() .
.
Ответы:
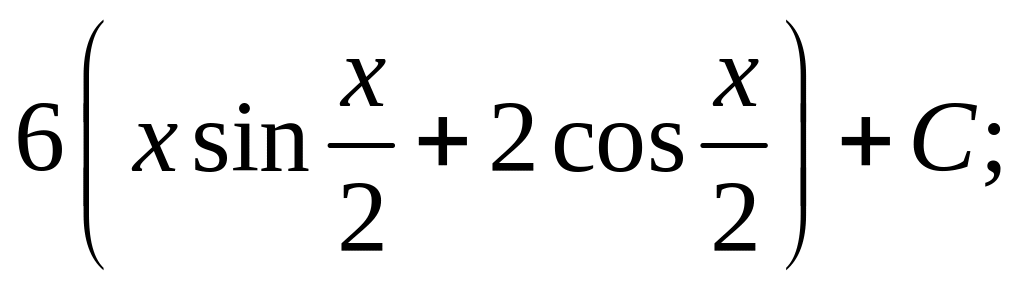 18)
18)
 ;
19)
;
19)

20)![]() 21)
21) ![]() ;
22)
;
22) ![]() ;
;
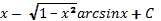 ;
24)
;
24)
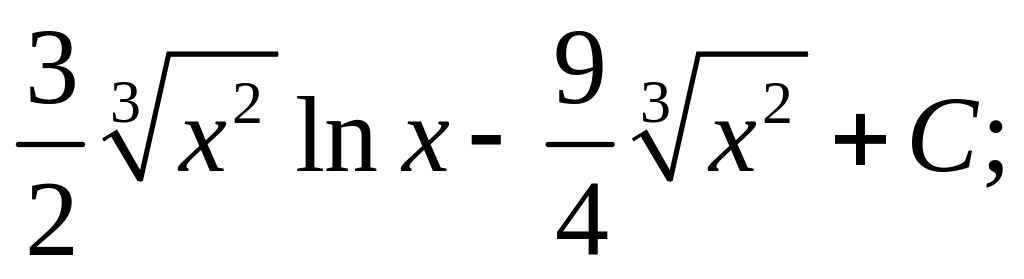 25)
25)
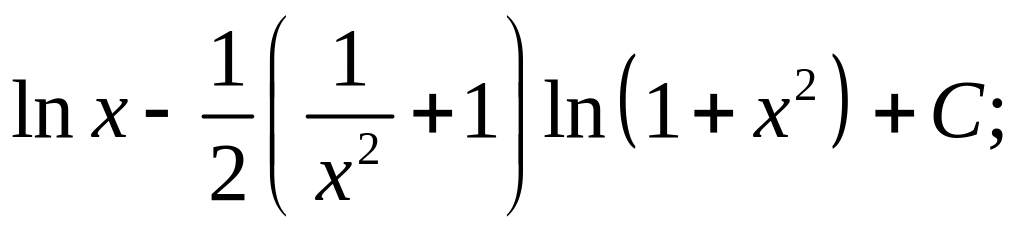
26)
![]() 27)
27)
![]() 28)
28)
![]()
Практическое занятие №14.
Интегрирование рациональных функций.
Контрольные вопросы.
1.Каков общий вид
целой рациональной функции (полинома)
степени n ![]() (x)?
(x)?
2. Что называется корнем (нулем) функции (x)?
3. На какие множители разлагается полином n-ой степени с вещественными коэффициентами?
4. Какие корни называются простыми; какие корни называются кратными?
5. Какого вида дроби называются простейшими?
6. К каким четырем типам интегралов приводит интегрирование правильной рациональной дроби?
7. В чем состоит метод неопределенных коэффициентов и метод частных значений?
Сформулируйте общее правило интегрирования рациональной дроби.
Примеры с решениями:
Найти интегралы:
1) I=
Подынтегральная функция – неправильная дробь. Выделим целую часть в правильной дроби.
Разложим знаменатель на множители:
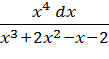 =
= ![]() +
+ 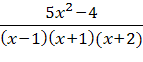
Разложим на простейшие правильную дробь:
= ![]() +
+ ![]() +
+ ![]() .
.
Освободимся от
знаменателей, умножив обе части на ![]()
5![]() .
.
Коэффициенты A, B, C найдем методом частных значений, давая x значения, равные корням знаменателя:
x = 1 5 ∙ 1
= 1 5 ∙ 1![]() 4
= A(1 + 1) (1 + 2)
4
= A(1 + 1) (1 + 2) ![]() A =
A = ![]()
x
= ![]() 5 ∙ 1
4
= B(
5 ∙ 1
4
= B(![]() (
(![]() B =
B =![]()
![]()
x
= ![]() 5 ∙ 4
4
= C(4
5 ∙ 4
4
= C(4![]()
![]() C
=
C
= ![]() .
.
Итак,
I = ![]() +
+ ![]() -
- ![]() +
+ ![]() = =
= =![]() .
.
2) I
= 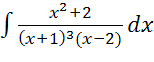 .
.
Подынтегральная функция – правильная рациональная дробь. Корни знаменателя вещественные:
x=2
– простой; x=![]() - кратности 3. Разложение на простейшие
принимает вид:
- кратности 3. Разложение на простейшие
принимает вид:
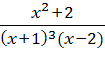 =
= ![]() +
+ 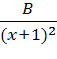 +
+ 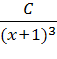 +
+ ![]()
Освобождаемся от знаменателей:
![]()
К оэффициенты
разложения определяем методом частных
значений, придавая x
любые значения, в том числе
оэффициенты
разложения определяем методом частных
значений, придавая x
любые значения, в том числе ![]() =
=![]() и
= 2 (корни знаменателя):
и
= 2 (корни знаменателя):
x
=
1 + 2 = C(![]()
x
= 2 4 + 2 = D![]()
![]() D
=
D
= ![]()
![]()
![]()
Последняя система принимает вид:
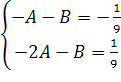
![]() A
=
A
=![]() , B
=
, B
= ![]() .
.
Итак, I
= 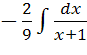 +
+ 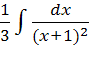
![]()
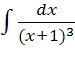 +
+ 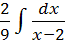 =
= ![]()
![]()
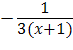 + +
+ + +
+ ![]() + c
= с
+ c
= с
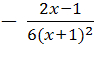 +
+ 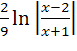 .
.
3) I
= 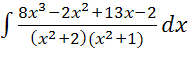 .
.
Подынтегральная функция – правильная рациональная дробь. Знаменатель представляет произведение простых квадратичных множителей (вещественных корней нет). Разложение дроби принимает вид:
 =
= ![]() +
+ ![]() .
.
Освобождаясь от знаменателей, получаем
8![]() = (A
= (A![]() + B)(
+ B)(![]() +1)
+ (C
+ D)(
+2).
+1)
+ (C
+ D)(
+2).
Коэффициенты находим методом неопределенных коэффициентов, приравнивая коэффициенты при одинаковых степенях :

![]() 8 = A + C A + C = 8
8 = A + C A + C = 8
![]() = B + D A + 2C = 13 A = 3, C = 5
= B + D A + 2C = 13 A = 3, C = 5
![]() 13 = A + 2C B + D =
13 = A + 2C B + D =
![]() = B + 2D B + 2D =
B =
,
D = 0.
= B + 2D B + 2D =
B =
,
D = 0.
Итак, I
= 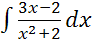 + 5
+ 5 =
= ![]()
![]() arctg
arctg![]() +
+ ![]() .
.
Примеры для практических занятий:
Найти интегралы:
4)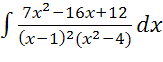 ; 5)
; 5) ;
;
6)
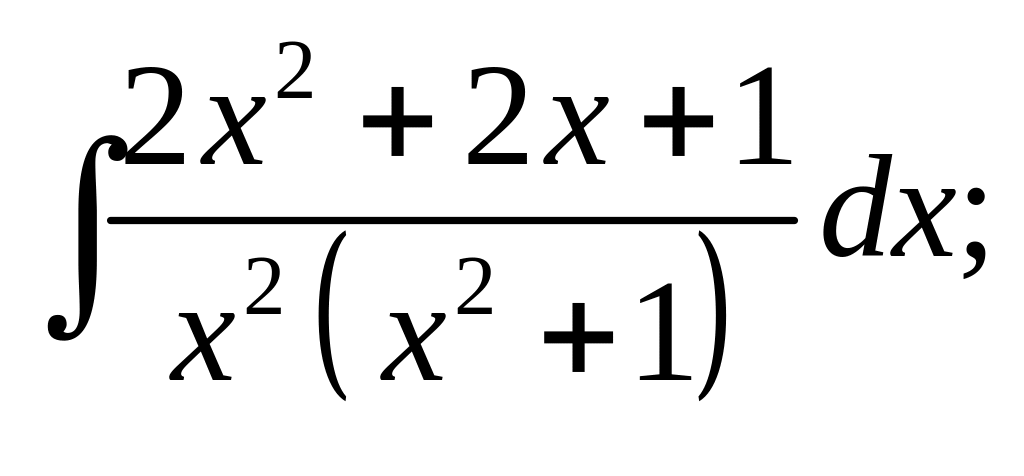 7)
7)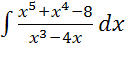 ;
;
8)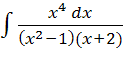 ; 9)
; 9)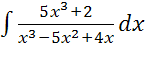 ;
;
10)
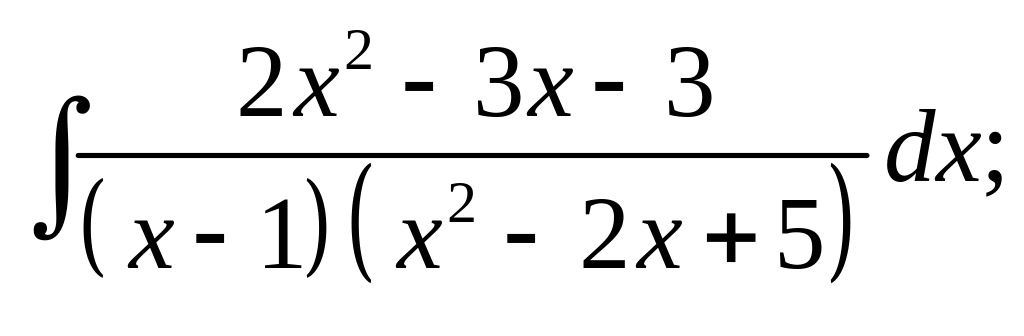 11)
11) .
.
Ответы:
4) ![]() + 2
+ 2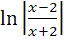 + c;
+ c;
2
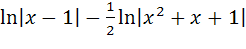 +
+
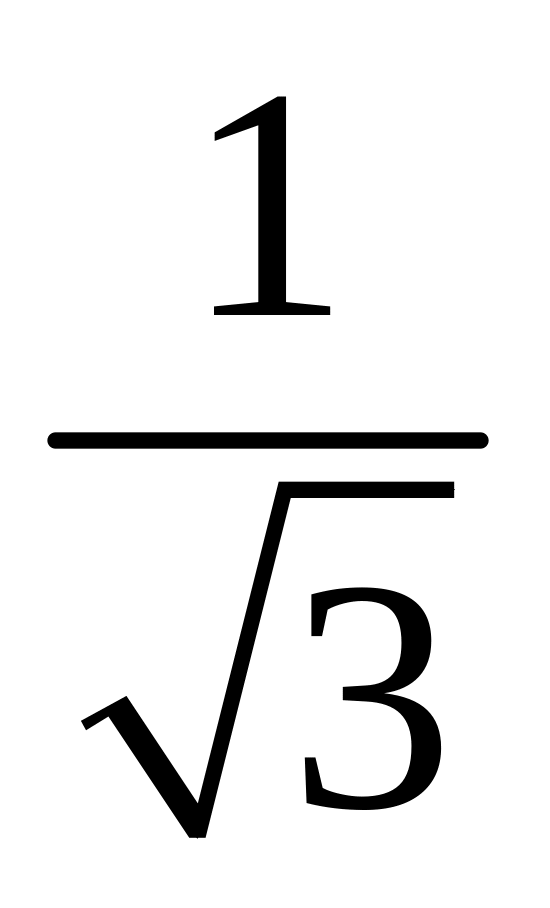 arctg
arctg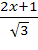 + c;
+ c;
6)![]() +
+ 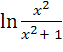 + arctgx+
c;
+ arctgx+
c;
7)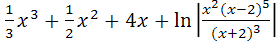 + c;
+ c;
8)![]() + c;
+ c;
9)
![]()
10)
![]() arctg
arctg![]() + c;
+ c;
11) ![]() arctg
arctg![]() + arctg(
+ arctg(![]() + c.
+ c.
Примеры для самостоятельного решения:
Найти интегралы:
12) 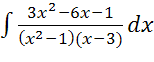 ; 13)
; 13) ![]() ; 14)
; 14) 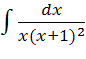 ;
;
15)
![]() 16)
16) 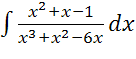 ; 17)
; 17) 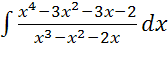 ;
;
18) ![]() ; 19)
; 19) ![]() ; 20)
; 20) ![]() ;
;
21) 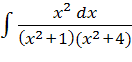 ; 22)
; 22) .
.
Ответы:
12) ![]() ; 13)
; 13) 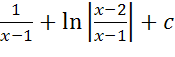 ;
;
14)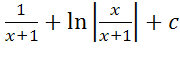 ; 15)
; 15) ;
;
16) ![]() ; 17)
; 17)
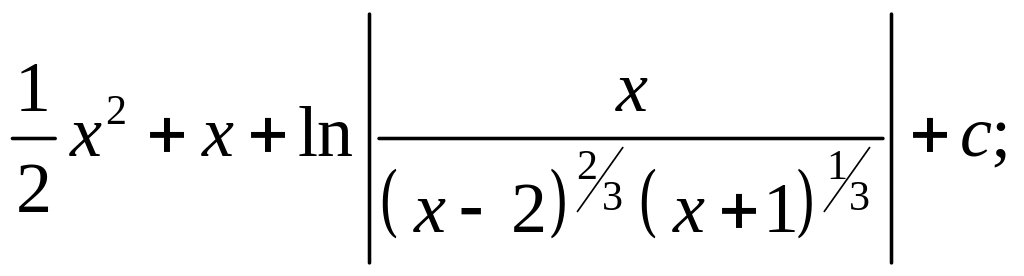
18) 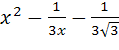 arctg
arctg![]() ; 19)
; 19) 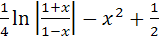 arctg
x+с
;
arctg
x+с
;
20)
 21)
21)![]() arctg
arctg
![]() arctg
x+c ;
arctg
x+c ;
22) ![]() arctg
(x
2)
+ с.
arctg
(x
2)
+ с.
Практическое занятие №15.
Интегрирование тригонометрических функций, рациональных относительно синуса и косинуса.
Контрольные вопросы.
Какой подстановкой
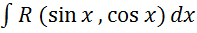 ,
где R- рациональная
функция, сводится к интегралу от
рациональной функции относительно
новой переменной?
,
где R- рациональная
функция, сводится к интегралу от
рациональной функции относительно
новой переменной?В каких случаях
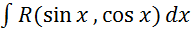 может быть взят с помощью подстановки
t=
может быть взят с помощью подстановки
t=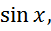 t=
t=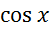 ,
t=
,
t=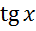 ?
?Как берутся интегралы
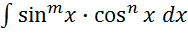 ,
где m и n-
целые числа?
,
где m и n-
целые числа?Как интегрируется произведения синусов и косинусов различных аргументов?
Примеры с решениями:
Найти J=
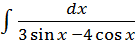 .
.
Так как подынтегральная
функция рациональна относительно ![]() ,
то воспользуемся универсальной
подстановкой.
,
то воспользуемся универсальной
подстановкой.
J=![]() =
=
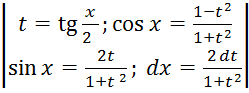 =
=
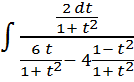 =
= 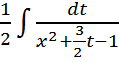 =
=
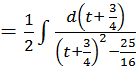 =
=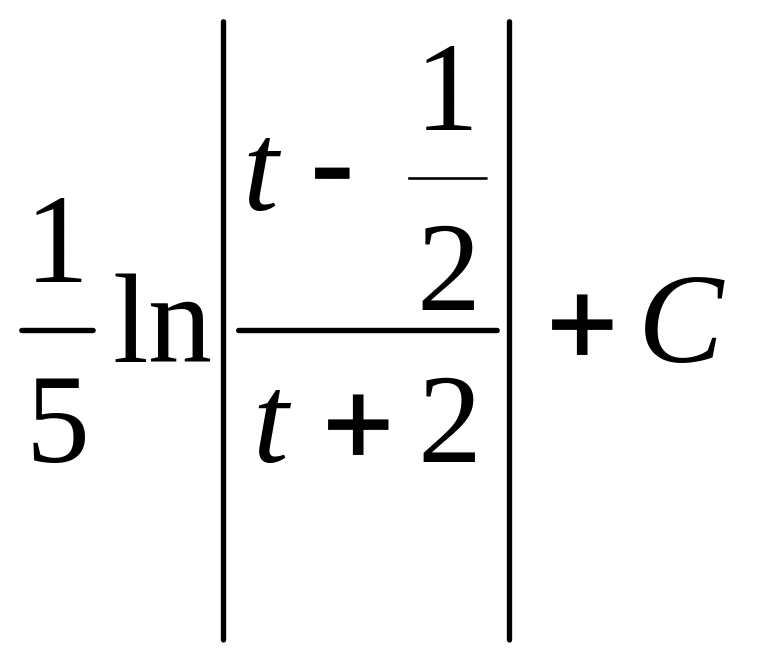 =
=
 +C.
+C.
Найти J
 .
.
Подынтегральная
функция нечетна относительно
.
Применим подстановку t=
![]() (
(![]()
J=![]()
![]() 3
3![]()
3) Найти J=![]() .
.
Подынтегральная
функция нечетна относительно
,
поэтому подстановка t=
(![]() ).
).
J=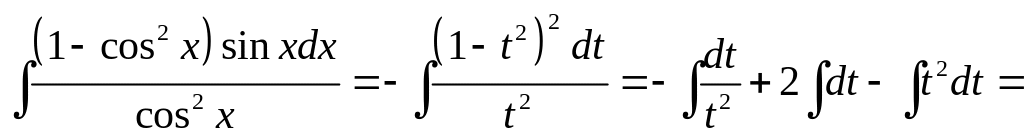
![]()
4) Найти J=![]() .
.
Подынтегральная
функция четна относительно ![]() поэтому подстановка
поэтому подстановка ![]() .
.
J=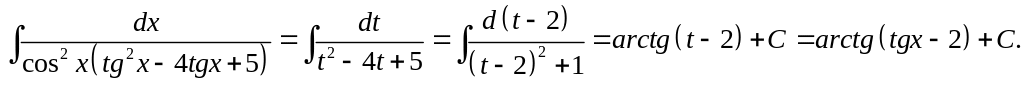
5) Найти
![]()
Подынтегральная
функция четна относительно ![]() ,
поэтому можно использовать подстановку
t=tgx.
Однако удобнее воспользоваться известными
формулами понижения степени
,
поэтому можно использовать подстановку
t=tgx.
Однако удобнее воспользоваться известными
формулами понижения степени ![]()
Тогда
J=![]()
=![]()
![]()
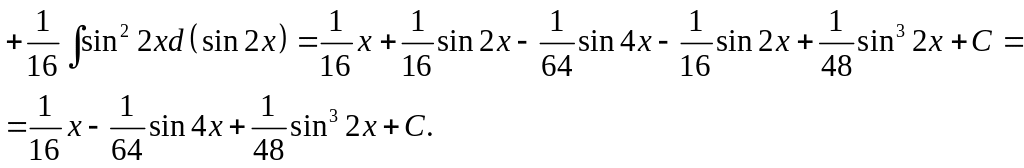
6)Найти J=![]() .
.
Воспользуемся формулами преобразования произведения тригонометрических функций в сумму или разность:
J=![]()
Примеры для практических занятий:
Найти интегралы:
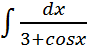 ;
;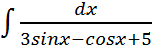 ;
;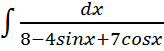 ;
;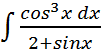 ;
;
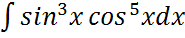 ;
;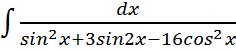 ;
;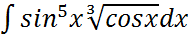 ;
;
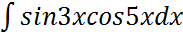 .
.
Ответы:
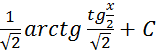 ;
;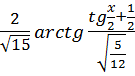 +С;
+С; +C
+C ;
; ;
;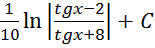 ;
;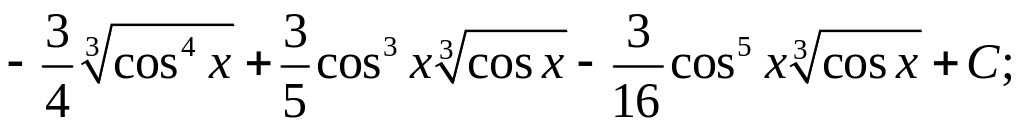
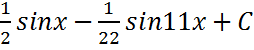 ;
; .
.
Примеры для самостоятельного решения:
![]() ;
;
![]() ;
;
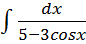 ;
;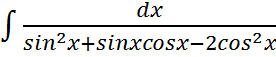 ;
;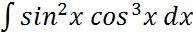 ;
; ;
;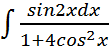 ;
;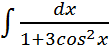 ;
;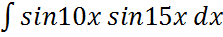 ;
;
 .
.
Ответы:
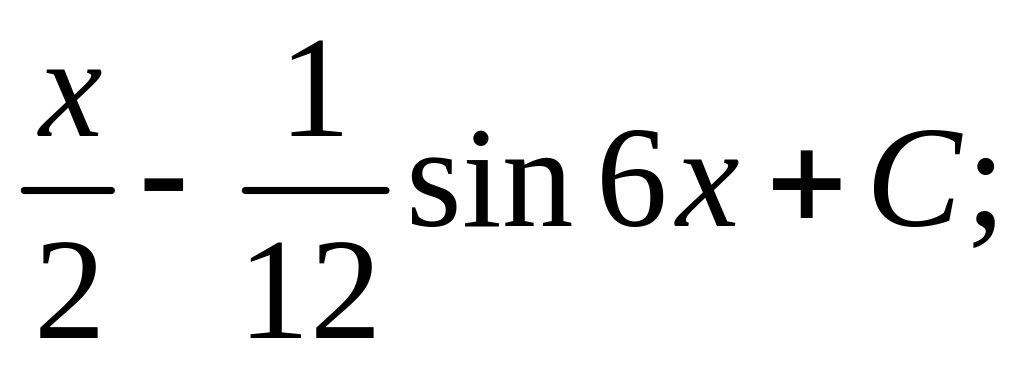
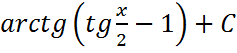 ;
;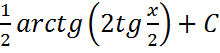 ;
; ;
;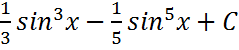 ;
;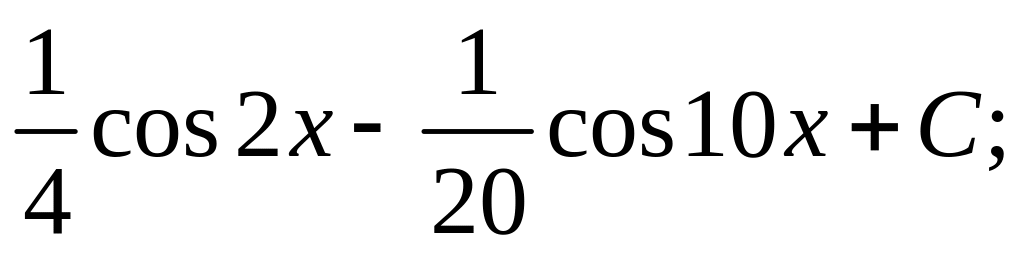

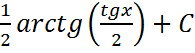 ;
;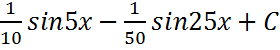 ;
;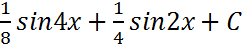 .
.
Практическое занятие №16.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Контрольные вопросы.
Дайте определение интегральной суммы f(x) на [a;b].
Сформулируйте определение определенного интеграла.
В чем состоит геометрический смысл определенного интеграла?
Перечислите основные свойства определенного интеграла.
В чем состоит свойство интеграла с переменным верхним пределом?
Запишите и прочтите формулу Ньютона-Лейбница.
В чем суть метода интегрирования подстановкой?
Каким условиям должна удовлетворять (и почему?) функция x=φ(t), используемая в качестве подстановки?
Примеры с решениями.
найти производные по х от следующих функций:
Решение:
Пользуясь правилом дифференцирования сложной функции и теоремой о производной интеграла с переменным верхним пределом, получим:
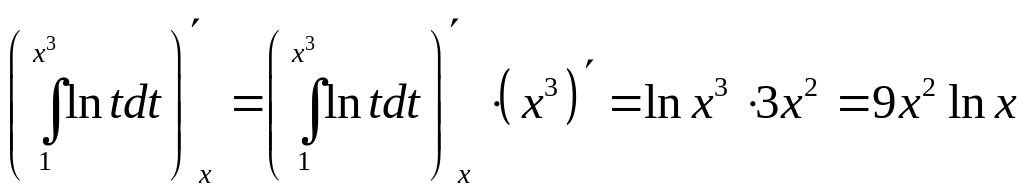
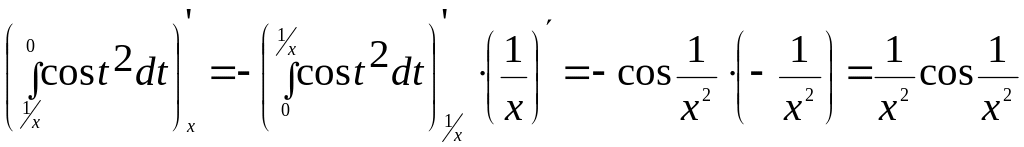
Представим заданный интеграл в виде:
 ,
где
С – произвольная постоянная.
Тогда:
,
где
С – произвольная постоянная.
Тогда:

Применяя формулу Ньютона – Лейбница, вычислить интегралы:
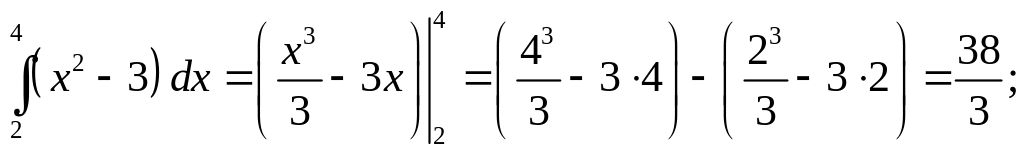
;
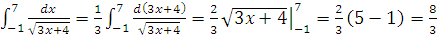 ;
;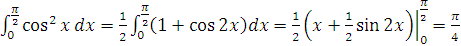 .
.
Применяя подходящую подстановку, вычислить интегралы:
а)
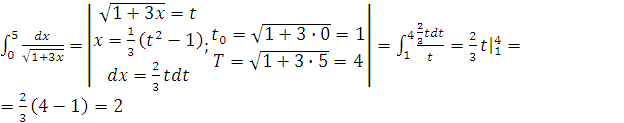
b)
=
c)![]() ;
;
d)
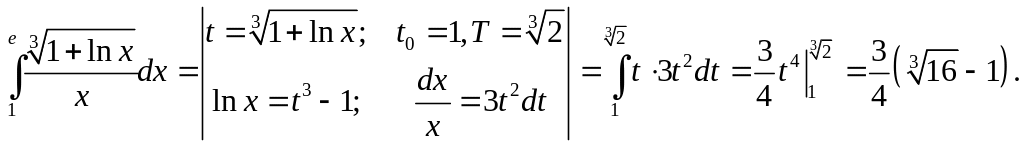
Примеры для практических занятий:
Вычислить интегралы:
4)![]() ;
5)
;
5)![]() ;
6)
;
6) ![]() ;
7)
;
7)![]() ;
;
8)![]() ;
9)
;
9) ![]() ;
10)
;
10)![]() ;
11)
;
11)![]() ;
;
12) ![]() ;
13)
;
13) ![]() ;
14)
;
14) ![]() ;
15)
;
15)![]() ;
;
16)![]() ;
17)
;
17)![]() ;
18)
;
18) ![]() .
.
Ответы:
4) ![]() ;
5)
;
5) ![]() ;
6)
;
6) ![]() ;
7)
;
7) ![]() ;
8)
;
8) ![]() ;
9)
;
9) ![]() ;
10)
;
10) 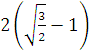 ;
;
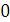 ;
12)
;
12) 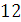 ;
13)
;
13) 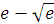 ;
14)
;
14) 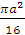 ;
15)
;
15) 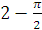 ;
16)
;
16) 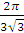 ;
17)
;
17) 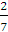 ;
18)
;
18) 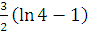 .
.
Примеры для самостоятельного решения.
19) Найти производные следующих функций:
a)
![]() ;
;
b)![]() ;
;
c)![]()
Вычислить интегралы:
20)![]() ;
21)
;
21)![]() ;
22)
;
22)![]() ;
23)
;
23) ![]() ;
;
24) ![]() ;
25)
;
25)![]() ;
26)
;
26)![]() ;
27)
;
27) ![]() ;
28)
;
28)![]() ;
;
29)![]() ;
30)
;
30)![]() ;
31)
;
31)![]() ;
32)
;
32)![]() ;
;
33)![]() .
.
Ответы:
19)a)![]() ; b)
; b)
![]() ; c)
; c)
![]() 20)
20)
![]() ;
21)
;
21) ![]() ;
22)
;
22) ![]() ;
23)
;
23)![]() ;
24)
;
24)![]() ;
25) 0; 26)
;
25) 0; 26) ![]() ;
27)
;
27)![]() ;
;
28) ![]() ;
29)
;
29)![]() ;
30)
;
30)![]() ;
31)
;
31)
![]() 32)
32)
![]() 33)
33)
![]()
Практическое занятие №17.
Определенный интеграл (продолжение).
Контрольные вопросы.
Записать и прочесть формулу интегрирования по частям в определенном интеграле.
Перечислить основные типы интегралов, вычисляемых по формуле интегрирования по частям.
Указать, какая часть подинтегральной функции принимается за U(x), а какая за dV(x).
Записать формулу интегрирования четных и нечетных функций по промежутку, симметричному относительно начала координат. Дать их геометрическую трактовку.
Указать различные варианты вычисления площадей плоских фигур в декартовых координатах.