- •Введение
- •1 Расчёт параметров нелинейной электрической цепи
- •1.1 Описание состояния электрической цепи с помощью законов Ома и Кирхгофа
- •1.2 Основные правила преобразования схем электрических цепей
- •1.3Методы решения нелинейных уравнений
- •1.4 Организация решения нелинейных уравнений в программах для работы с электронными таблицами MicrosoftExcel и OpenOfficeCalc
- •1.5 Контрольные вопросы
1.2 Основные правила преобразования схем электрических цепей
В электрических цепях основными способами соединения элементов являются последовательное и параллельное.
Последовательное соединениеобразуется путём соединения нескольких элементов таким образом, что включающий их участок цепи не имеет ни одного узла. То есть внутри участка в одной точке могут соединяться только две ветви.
На рисунке 4 приведён пример последовательного соединения резистивных (а), ёмкостных (б) и индуктивных (в)элементов.

Рисунок 4 – Последовательное соединение элементов цепи.
При последовательном соединении проводников сила тока во всех проводниках одинакова. Для случаев, приведённых на рисунке 4, будут справедливы равенства:
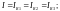
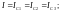
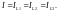 (5)
(5)
Падение напряжения на участке цепи равно сумме падений напряжений на последовательно соединённых элементах цепи:
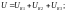
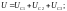
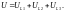 (6)
(6)
Для нахождения суммарных значений сопротивления, индуктивности и ёмкости при последовательном соединении элементов используются следующие выражения:
 (7)
(7)
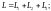 (8)
(8)
 (9)
(9)
Параллельное соединение образуется путём объединения всех входящих в цепь элементов двумя узлами.
На рисунке 5 приведён пример параллельного соединения резистивных (а), индуктивных (б) и ёмкостных (в) элементов.
Рисунок 5 – Параллельное соединение элементов цепи.
При параллельном соединении проводников напряжениена всех участках цепи одинаково. Для случаев, приведённых на рисунке 5, будут справедливы равенства:
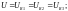
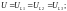
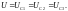 (10)
(10)
Силу тока на разных участках цепи при их параллельном соединении можно определить по закону токов Кирхгофа. В результате для рассматриваемых случаев получим следующие выражения:

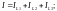
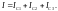 (11)
(11)
Для нахождения суммарных значений сопротивления, индуктивности и ёмкости при параллельном соединении элементов используются следующие выражения:
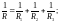 (12)
(12)
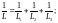 (13)
(13)
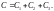 (14)
(14)
В общем случае соединение отдельных участков цепи может быть более сложным и приведённые закономерности для последовательного и параллельного соединения использовать без предварительного преобразования оказывается затруднительно. Такими преобразованиями являются «треугольник – звезда» и «звезда – треугольник». Схемы треугольника и звезды приведены на рисунке 6.
Для перехода от треугольника к звезде используются следующие выражения:
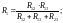 (15)
(15)
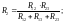 (16)
(16)
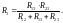 (17)
(17)

Рисунок 6 – Схемы треугольника и звезды.
Для перехода от звезды к треугольнику используются следующие выражения:
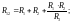 (18)
(18)
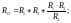 (19)
(19)
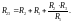 (20)
(20)
1.3Методы решения нелинейных уравнений
Линейным уравнением называют такое, обе части которого могут быть выражены многочленами (от неизвестных) первой степени. Если это требование не выполняется, то уравнение называют нелинейным. Нелинейные уравнения можно разделить на несколько характерных групп. Если не учитывать специальные виды исчислений (например, интегральное, дифференциальное и т.п.), то нелинейные уравнения можно разделить на две большие группы:
– нелинейные алгебраические уравнения;
– трансцендентные уравнения.
Нелинейное алгебраическое уравнение может содержать только алгебраические функции, в которых над переменной x проводятся арифметические операции, возведение в степень с рациональным показателеми извлечение корня.Трансцендентнымназывается уравнение, в состав которого входят трансцендентные функции: показательная, логарифмическая, тригонометрические функции, возведение в иррациональную степень.
В самом простом случае на практике приходится решать уравнения с одним неизвестным. В данном разделе будут рассматриваться только такие уравнения. Если неизвестных в уравнении несколько, то для решения необходимо получить систему уравнений с числом уравнений, равным числу неизвестных. Если число уравнений больше или меньше числа неизвестных получить единственное решение нельзя. В таком случае говорят, что имеет место бесконечное множество решений.
Для уравнений с одним неизвестным на практике используются различные методы решения, которые можно разделить на две большие группы:
– точные методы решения;
– методы численного решения.
Точные методы решения базируются на использовании готовых формул. Такие формулы разработаны для уравнений до четвёртого порядка включительно.
В случае если получить решение точным методом затруднительно или невозможно (для уравнений высоких порядков), то пользуются методами численного решения. Численное решение уравнения f(x) = 0 (речь идёт о действительных корнях) проводят в два этапа:
– отделение корней, т. е. отыскание таких достаточно малых отрезков в области допустимых значений x, в которых содержится только один корень;
– уточнение корней, т. е. вычисление корней с заданной точностью.
На практике используются следующие способы отделения корней:
– по графику функции;
– замена исходного уравнения равносильным;
– по таблице значений функции на интересующем интервале изменения аргумента;
– аналитический метод отделения корней.
Способ отделения корней по графику функции y = f(x).
К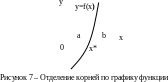 орень
уравненияf(x)=0приближенно
определяется как абсцисса точки
пересечения графика с осью 0x
(рисунок7). Устанавливаются границы a
и b
отрезка, в пределах которого заключён
только один корень x*.
орень
уравненияf(x)=0приближенно
определяется как абсцисса точки
пересечения графика с осью 0x
(рисунок7). Устанавливаются границы a
и b
отрезка, в пределах которого заключён
только один корень x*.
Способ отделения корней заменой исходного уравнения равносильным.
Исходное уравнение вида f(x)=0 приводят к видур(х)=q(х). Далее строят графики функций у1(х)=р(х) и у2(х)=q(х) и находят точку пересечения графиков, абсцисса которой приближённо будет равна корню уравнения.
Рассмотрим подробнее этот способ отделения корней на примере. Пусть имеется следующее уравнение:
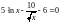 .
.
Преобразуем его к виду р(х)=q(х):
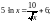
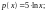
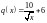 .
.
Построим графики этих функций (рисунок 8).

Рисунок 8 – Отделение корня по пересечению графиков составляющих равносильного уравнения.
В результате анализа графика установлено, что корень уравнения лежит в окрестностях х=7.
Способ отделения корней по таблице значений функции на интересующем интервале изменения аргумента.
Для исследуемой функции необходимо построить таблицу зависимости функции от аргумента. В таблице необходимо выявить интервалы, на которых меняется знак функции. Внутри таких интервалов лежат корни уравнения.
Рассмотрим этот способ на том же примере.Преобразуем уравнение к функции:
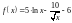 .
.
Построим таблицу значений для данной функции в диапазоне от 0 до 10 (таблица 1).
Таблица 1 – Значения аргумента и функции при отделении корней
х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
f(x) |
– |
-16 |
-9,61 |
-6,28 |
-4,07 |
-2,43 |
-1,12 |
-0,05 |
0,86 |
1,65 |
2,35 |
Анализируя таблицу 1 можно заметить, что знак функции меняется на интервале от 7 до 8.
Аналитический метод отделения корней базируется на знании следующих свойств функции:
если функция f(x)непрерывна на отрезке [а;b] и принимает на концах этого отрезка значения разных знаков, то внутри отрезка [а;b]существует по крайней мере один корень уравнения f(x)=0;
если функция f(x) непрерывна и монотонна на отрезке [а;b]и принимает на концах отрезка значения разных знаков, а производная f’(x) сохраняет постоянный знак внутри отрезка, то внутри этого отрезка существует корень уравнения f(x)=0 и притом единственный.
Функция y=f(x) называется монотонной в заданном интервале, если при любых x2>x1 из этого интервала она удовлетворяет условию f(x2)>f(x1) (монотонно возрастающая функция) или f(x2)<f(x1) (монотонно убывающая функция).
Необходимым и достаточным условием монотонности функции в заданном интервале является выполнение для всех внутренних точек этого интервала условия f’(x)≥0 или f’(x)≤0.
После отделения корней переходят к уточнению корней, которое может проводиться различными методами. Наибольшее распространение получили следующие:
– метод половинного деления (дихотомии);
– метод Ньютона;
– метод итерации (последовательного приближения).
Метод половинного деления.
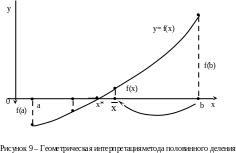
Дано уравнение в форме f(x)=0. Функция f(x) непрерывна и монотонна на отрезке [а;b] и имеет на концах отрезка разные знаки. Требуется найти корень x* уравнения с точностью до ε. График функции представлен на рисунке9. Алгоритм уточнения корня по этому методу следующий:
–отрезок [а;b]нужно разделитьпополам.Определяем середину отрезка по выражению
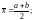 (21)
(21)
–вычислить
значение функции в точке
 .
Если
.
Если
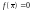 ,
то
является
корнем уравнения. Если
,
то
является
корнем уравнения. Если
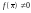 ,
то поиск корня продолжается на одном
из двух полученных отрезков – [а;
]или
[
;b].
Следует выбрать тот отрезок, на концах
которого функция f(x)
принимает значения противоположных
знаков. В нашем случае (рисунок9) выбираем
отрезок [а;
],
так как для него выполняется условие
наличия на концах отрезка разных
знаков.Для того чтобы сохранить в
дальнейших расчётах единое обозначение
[а;b]
текущего отрезка, на котором ведётся
поиск корня на данном шаге вычислений,
необходимо параметру b
присвоить новое значение
:
b=
.
С точки зрения геометрической
интерпретации (рисунок 9) это означает,
что правая граница исходного отрезка
точка b
переносится в точку
,
а оставшаяся за пределами точки
часть графика дальше не рассматривается;
,
то поиск корня продолжается на одном
из двух полученных отрезков – [а;
]или
[
;b].
Следует выбрать тот отрезок, на концах
которого функция f(x)
принимает значения противоположных
знаков. В нашем случае (рисунок9) выбираем
отрезок [а;
],
так как для него выполняется условие
наличия на концах отрезка разных
знаков.Для того чтобы сохранить в
дальнейших расчётах единое обозначение
[а;b]
текущего отрезка, на котором ведётся
поиск корня на данном шаге вычислений,
необходимо параметру b
присвоить новое значение
:
b=
.
С точки зрения геометрической
интерпретации (рисунок 9) это означает,
что правая граница исходного отрезка
точка b
переносится в точку
,
а оставшаяся за пределами точки
часть графика дальше не рассматривается;
–новый отрезок [а;b] снова делится пополам по выражению (21);
–вычисляется f(x) и проводится анализ двух вновь полученных отрезков – [а; ]и [ ;b]. Выбирается тот из них, для которого выполняется условие противоположности знаков функции в граничных точках;
–процесс деления пополам текущего отрезка необходимо продолжать до тех пор, пока очередной отрезок [а;b] не будет удовлетворять условию:
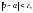 (22)
(22)
где ε – требуемая точность расчёта.
За приближённое значение корня x* принимаем значение середины последнего отрезка [а;b], т. е.
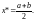 (23)
(23)
Метод Ньютона.
Требуется решить уравнение , причём f’(x) и f”(x) определены, непрерывны и сохраняют постоянные знаки на отрезке [а;b].
Рассмотрим алгоритм метода Ньютона на основе его геометрической интерпретации (рисунок 9):
–выбираем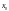 –
начальное приближение корня x*,
соблюдая следующее правило: за начальное
приближение корня необходимо принять
тот конец отрезка[а;b],
в котором знак функции совпадает со
знаком второй производной, т.е. выполняется
условие:
–
начальное приближение корня x*,
соблюдая следующее правило: за начальное
приближение корня необходимо принять
тот конец отрезка[а;b],
в котором знак функции совпадает со
знаком второй производной, т.е. выполняется
условие:
 (24)
(24)
Выражение (24) является условием сходимости метода Ньютона.

Для
рассматриваемой функции (рисунок 9)
f(x)можно
сделать вывод о выполнении условия
сходимости для точки b.Принимаем
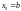 ;
;
–вычисляем
значение функцииf(x0).
Проводим касательную к кривой f(x)в
точке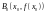 .
Абсцисса точки пересечения касательной
с осью Оx
принимается за новое (первое) приближение
корня x1.
.
Абсцисса точки пересечения касательной
с осью Оx
принимается за новое (первое) приближение
корня x1.
Уравнение касательной, проведенной в точке B0 с координатами (x0,f(x0)) к кривой функции f(x), имеет вид:
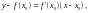 (25)
(25)
где x, y – текущие координаты точки, лежащей на касательной.
Для точки x1 сделаем подстановку в уравнение касательной (25):
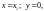 (26)
(26)
и получаем:
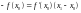 (27)
(27)
После преобразования уравнения (27) и выражения x1 получим:
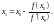 (28)
(28)
–вычисляем
значение функции f(x)
в точке x1,
проводим касательную к кривой f(x)
в точке
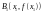 .
Абсцисса точки пересечения касательной
с осью Оx
представляет собой второе приближение
корня x2:
.
Абсцисса точки пересечения касательной
с осью Оx
представляет собой второе приближение
корня x2:
 (29)
(29)
–продолжаем последовательно проводить касательные и определять точки их пересечения с осью Оx. Тогда для текущего k-го приближения корня итерационный процесс реализуется рекуррентной формулой:
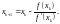 (30)
(30)
Процесс уточнения корня прекращается при выполнении условия близости двух последовательных приближений:
 (31)
(31)
Метод
Ньютона обладает высокой скоростью
сходимости, которая тем выше, чем больше
крутизна графика функции f(x)в
пределах рассматриваемого отрезка.
Если численное значение производной
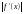 мало вблизи корня, то процесс уточнения
корня может оказаться очень долгим.
мало вблизи корня, то процесс уточнения
корня может оказаться очень долгим.
Неудачно выбранное начальное приближение может привести к расходимости метода (рисунок 9): представим, что за начальное приближение x0 принят левый конец отрезка a, касательная, проведенная в точке А0, пересекает ось Оx за пределами заданного отрезка [a,b]. Таким образом, получили первое приближение к корню ‹x1›, ещё дальше отстоящее от искомого значения корня x*, чем нулевое приближение x0.
Метод итерации (последовательных приближений).
В общем случае метод итерации прост и его алгоритм выглядит следующим образом.
Дано
уравнение
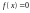 .
Для решения преобразуем его к виду:
.
Для решения преобразуем его к виду:
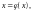 (32)
(32)
На заданном отрезке [a,b] выбираем начальное приближение корня x0. Подставляем его в правую часть уравнения (32) и получаем первое приближение корня x1:
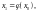 (33)
(33)
Аналогично определим второе приближение корня:
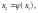 (34)
(34)
Продолжая этот процесс далее, получаем последовательность чисел х0, х1, х2, … , хn, определяемых соотношением:
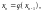 (35)
(35)
Итерационные вычисления продолжают до тех пор, пока для двух последовательных приближенийхn-1и хn не выполнится условие:
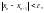 (36)
(36)
Достаточным условием сходимости метода итерации, гарантирующим, что последовательно определяемые значения х1, х2, х3, … , хn будут приближаться к искомому корню уравнения x*, является условие:
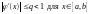 (37)
(37)
причём скорость сходимости будет тем больше, чем меньше число q.
Рассмотрим
геометрическую интерпретацию метода
итерации.
Исходное уравнение
приводим к виду (32).Строим графики функций
y=x
и
 .
Абсцисса точки пересечения этих графиков
и будет являться корнем x*
уравнения f(x)=0.
.
Абсцисса точки пересечения этих графиков
и будет являться корнем x*
уравнения f(x)=0.
Рассмотрим основные возможные варианты итерационного процесса.
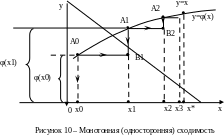
Вариант
1.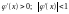 (рисунок10).
(рисунок10).
Задаём
начальное приближение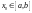 .
Определяем
.
Определяем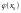 .
Через точку А0
с координатами
.
Через точку А0
с координатами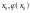 проводим горизонтальную линию до
пересечения с прямой y=x
в точке В1.
Через точку В1
проводим вертикальную линию, пересекающую
кривую
и ось Оx.
Точка пересечения этой линии с осью Оx
даст первое приближение корня x1,
а точка пересечения её с кривой
– точку А1
с координатами
проводим горизонтальную линию до
пересечения с прямой y=x
в точке В1.
Через точку В1
проводим вертикальную линию, пересекающую
кривую
и ось Оx.
Точка пересечения этой линии с осью Оx
даст первое приближение корня x1,
а точка пересечения её с кривой
– точку А1
с координатами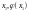 .
Через точку А1
проводим горизонтальную линию до
пересечения с прямой y=x
(точка В2).
Вертикальная линия, проведенная через
точку В2,
пересекая ось Оx,
даст второе приближение корня x2,
а также определит на кривой
точку
А2
с
координатами
.
Через точку А1
проводим горизонтальную линию до
пересечения с прямой y=x
(точка В2).
Вертикальная линия, проведенная через
точку В2,
пересекая ось Оx,
даст второе приближение корня x2,
а также определит на кривой
точку
А2
с
координатами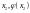 Продолжая действия по такой же схеме,
получаем на оси Оx
последовательность значенийх0,
х1,
х2,
… , приближающихся(сходящихся) к истинному
значению корня x*.
Причём все последовательные приближения
находятся с одной стороны от корня x*.
Такая сходимость называется монотонной
или односторонней.
Продолжая действия по такой же схеме,
получаем на оси Оx
последовательность значенийх0,
х1,
х2,
… , приближающихся(сходящихся) к истинному
значению корня x*.
Причём все последовательные приближения
находятся с одной стороны от корня x*.
Такая сходимость называется монотонной
или односторонней.
Вариант
2. (рисунок
11). Итерационный процесс расходится.
(рисунок
11). Итерационный процесс расходится.
Вариант
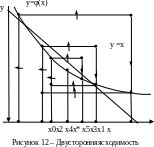
3.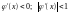 (рисунок12). Итерационный процесс сходится.
Процесс сходимости носит колебательный
характер (двусторонняя сходимость).
(рисунок12). Итерационный процесс сходится.
Процесс сходимости носит колебательный
характер (двусторонняя сходимость).
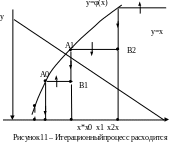
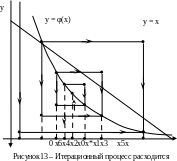
Вариант
4.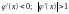 (рисунок13).
Итерационный процесс расходится.
(рисунок13).
Итерационный процесс расходится.
Преобразование
исходного уравнения
к уравнению (32) может быть осуществлено
различными способами. Выбор конкретного
способа определяется целью – получить
такую функцию
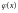 ,
длякоторой выполняется (37). Рассмотрим
несколько примеров.
,
длякоторой выполняется (37). Рассмотрим
несколько примеров.
Требуется найти корень уравнения 2x3–10x+5=0 на отрезке [0, 1].
Способ 1 – прибавляем к обеим частям исходного уравнения x. В нашем случае получаем
2x3–10x+5+х=х.
После преобразований получаем
2x3–10x+5=х.
Отсюда
 .
.
Проверяем, выполняется ли условие сходимости на отрезке [0, 1]:
 ;
;
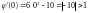 ;
;
 .
.
Условие сходимости не выполняется, следовательно, функция в таком виде непригодна.
Способ 2 – выражаем x из исходного уравнения:
11x=2x3+5.
Получаем:
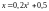 .
.
Следовательно,
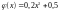 .
.
Проверяем, выполняется ли условие сходимости на отрезке [0, 1]:
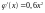 ;
;
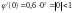 ;
;
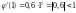
Условие
сходимости на
заданном отрезкевыполняется. Значит
можно воспользоваться для процесса
итерации функцией
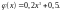
Способ 3 – левую и правую части исходного уравнения f(x)=0 умножаем на произвольную константу λ и прибавляем к обеим частям неизвестное x:
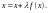 (38)
(38)
Тогда
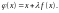 Коэффициент
λ задается следующим образом:
Коэффициент
λ задается следующим образом:
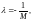 (39)
(39)
где
M
– наибольшее значение производной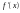 на отрезке [a,
b]:
на отрезке [a,
b]:
 (40)
(40)
В качестве примера рассмотрим решение уравнения х3+3х2–2=0, для которого нужно найти корна на интервале [0,5;1,5].
Представим рассматриваемое уравнение в следующем виде:
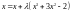 .
.
Следовательно,
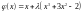 .
.
Определяем λ:
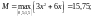
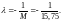
Таким образом,
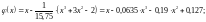
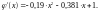
Проверим выполнение условия сходимости:
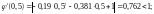
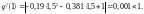
Условие сходимости выполняется.
Способ 4 – логарифмирование уравнение.
Рассмотрим
этот способ при решении уравнения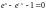 на отрезке [0;1].
Представим уравнение в виде
на отрезке [0;1].
Представим уравнение в виде
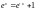 и прологарифмируем обе части:
и прологарифмируем обе части:
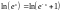 ;
;
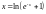 .
.
Значит
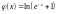 ;
;
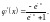
Выполним проверку условия сходимости процесса на исследуемом отрезке:
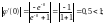
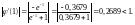
Условие сходимости выполняется.
Применим описанные методы для решения практической задачи.
И меется
цепь постоянного тока (рисунок 14),
включающая в себя последовательно
включённые источник энергии в виде
источника ЭДС, линейное сопротивление
и нелинейное сопротивление, которое
задаётся в виде функции напряжения от
тока.
меется
цепь постоянного тока (рисунок 14),
включающая в себя последовательно
включённые источник энергии в виде
источника ЭДС, линейное сопротивление
и нелинейное сопротивление, которое
задаётся в виде функции напряжения от
тока.
По закону напряжений Кирхгофа получаем
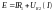 .
.
Зададимся
числовыми значениями и найдём протекающий
в цепи ток:Е=100
В, R1=10
Ом,
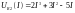 .
.
В результате получим:
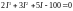 .
.
Выполним
отделение корней. Воспользуемся методом
построения таблиц. Границы интервала
поиска установим на положительной
полуоси: от 0 до
 А.
А.
Таблица 2 – Значения аргумента и функции при отделении корней
I |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
-100 |
-90 |
-62 |
-4 |
96 |
250 |
470 |
768 |
1156 |
1646 |
2250 |
Из таблицы 2 следует, что корень уравнения лежит в диапазоне от 3 до 4 А. Уточнение корней выполним по методу половинного деления с точностью до 0,001 А и сведём результаты в таблицу 3.
Таблица 3 – Уточнение корней
|
I |
|
I |
|
I |
|
Левая граница |
3 |
-4 |
3 |
-4 |
3 |
-4 |
Средина |
3,5 |
40 |
3,25 |
16,593 |
3,125 |
5,957 |
Правая граница |
4 |
96 |
3,5 |
40 |
3,25 |
16,593 |
Левая граница |
3 |
-4 |
3 |
-4 |
3,0312 |
-1,573 |
Средина |
3,0625 |
0,895 |
3,0312 |
-1,573 |
3,0468 |
-0,344 |
Правая граница |
3,125 |
5,95703 |
3,062 |
0,895 |
3,0625 |
0,895 |
Левая граница |
3,0468 |
-0,3442 |
3,0468 |
-0,3442 |
3,0507 |
-0,0353 |
Средина |
3,0546 |
0,274 |
3,0507 |
-0,0354 |
3,0527 |
0,1192 |
Правая граница |
3,0625 |
0,895 |
3,0546 |
0,2741 |
3,0546 |
0,2741 |
Левая граница |
3,05078 |
-0,0353 |
3,05078 |
-0,0353 |
3,0507 |
-0,035 |
Средина |
3,05175 |
0,0419 |
3,05127 |
0,0033 |
3,05102 |
-0,016 |
Правая граница |
3,05273 |
0,11928 |
3,05175 |
0,04197 |
3,05127 |
0,0033 |
В таблице 3 полужирным шрифтом показаны значения аргумента и функции границ интервала, используемые на следующем шаге уточнения. Анализируя результаты расчёта, представленные в таблице 3, приходим к выводу о том, что ток приблизительно равен I=3,0511 А.