10 ПриближЁнные методы решения задач теплопроводности. Методы аналогии

Решение дифференциального уравнения теплопроводности для наиболее простейшего случая одномерной задачи для пластины (9.9). На практике встречается многомерная задача теплопроводности для тел сложной формы, и получить аналитическое решение для таких сложных тел невозможно.

Когда задачу нельзя решить аналитически применяют численные или графические методы и методы аналогии, которые дают приближённое решение.

При аналитическом решении дифференциального уравнения теплопроводности можно определить температуру в любой точке исследуемого пространства. При численном методе вместо дифференциального уравнения используются алгебраические уравнения, по которым можно определить температуру только в отдельных узловых точках пространства. Следующие численные методы решения задач теплопроводности:

1. Метод конечных разностей (метод сеток);

2. метод конечных элементов;

3. метод прогонки;

4. метод переменных направлений;

5. метод расщепления;

6. метод суммарной аппроксимации и др.

В методе (1) область непрерывного изменения аргументов (x, y, z, ) заменяется сеткой, т.е. конечным множеством точек, которые называются узлами сетки. Разности значений одних и тех же элементов для двух смежных узлов (x, y, z, ) называют шагами сетки. Важнейшее свойство разностных схем – это аппроксимируемость, устойчивость и сходимость.

Аппроксимируемость схемы означает, что при стремлении к нулю шагов аргументов решение системы алгебраических уравнений стремится к решению исходного дифференциального уравнения.

Устойчивой называют такую схему, для которой неизбежной ошибки округления при уменьшении шагов аргумента не приводит к большим искажениям решения.

Сходимость означает, что при сгущении сетки решение системы алгебраических уравнений сводится к решению дифференциального уравнения.

Рассмотрим МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ для решения уравнения двухмерной стационарной теплопроводности. Без вывода покажем, что дифференциальное уравнение двухмерной теплопроводности сводится к алгебраическому уравнению вида:

. (10.1)

Координаты точки 0 – х, у; температура в точке 0 – Т₀, а температуры в узлах сетки Т₁, Т₂, Т₃, Т₄.

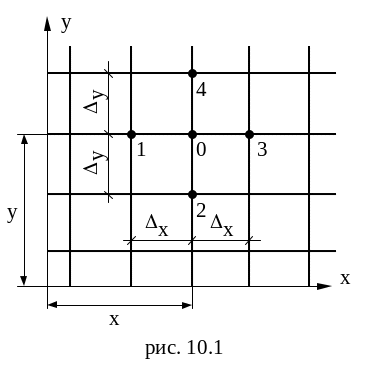
. (10.2)

Из (10.2) следует, что температура в любом узле есть среднее арифметическое температур в соседних четырёх узлах сетки.

Для трёхмерного температурного поля алгебраическое уравнение имеет вид: . (10.3)

.

Метод аналогии:

В тех случаях, когда аналитическое решение задачи теплопроводности невозможно, а численное громоздко, можно применить метод аналогии. Метод аналогии позволяет установить метод распределения температуры в исследуемом объекте по распределению другой легко измеряемой величины в модели объекта. Тогда математическое описание распределения температур и другой величины будут аналогичны.

Гидродинамическая аналогия. Рассмотрим возможность моделирования процесса двухмерной стационарной теплопроводности безвихревым потоком идеальной жидкости. Для идеальной жидкости известно следующее уравнение для функции тока

. (10.4)

Линии, для которых , называются линиями тока жидкости. Визуальная картина линий тока показана на рисунке (10.2).

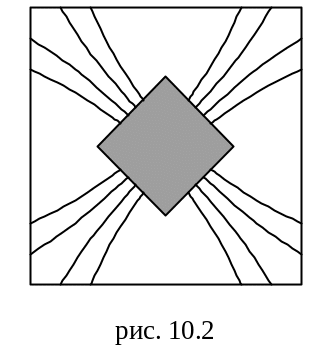
Линии тока можно сделать видимыми, вводя кристаллы перманганата калия, который, перемещаясь в растворе, оставляет следы по линиям тока.

Потенциал скоростей тока перпендикулярен линиям тока. Поэтому линии теплового потока и температурного потенциала при двухмерной стационарной теплопроводности аналогичны соответственно линиям тока и потенциала скоростей идеальной жидкости, следовательно, можно экспериментально по линиям тока построить линии теплового потока и построить изотермы, так как они перпендикулярны между собой.

Электрическая аналогия:

При разработке электрических моделей, эмитирующих процесс теплопроводности, применительны два способа:

1. Электрические модели повторяют геометрию оригинальных тепловых систем и изготавливаются из материала с непрерывной проводимостью. Согласно электрической аналогии напряжение в любой точке электрической модели соответствует температуре в той же точке теплового объекта.

2. Изготавливают модели с сосредоточенными параметрами процесса. В них тепловая система заменяется моделирующими электрическими цепями. Термическое сопротивление заменяется электрическим сопротивлением, а теплоёмкость электрическим конденсатором (ёмкостью).

Рассмотрим рисунок (10.3).

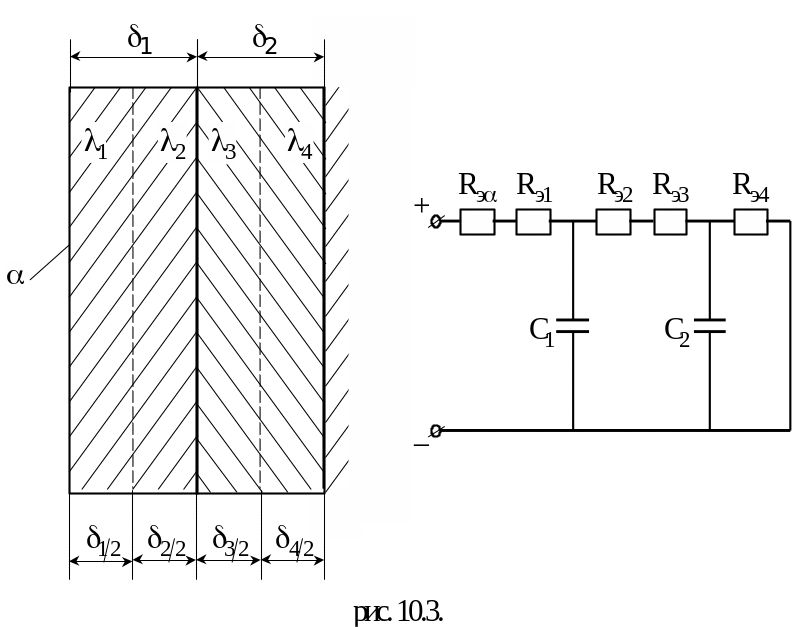
Одна сторона стены теплоизолированна, с другой стороны – коэффициент теплоотдачи . Каждый слой стены можно разбить на два слоя. Тогда внутренне термическое сопротивление может быть представлено в виде четырёх термических сопротивлений.

; ; ; .

­ – моделируется внешним электрическим сопротивлением R_ .

Последующее состояние моделируется путём приложения к зажимам контура «+», «–», и для произвольных моментов времени они будут соответствовать значениям температур в том же масштабе в сходственных точках схемы. Измерив напряжение с помощью вольтметра в любой точке схемы, можно определить значение температуры в любой точке объекта в масштабе.