
- •Линейные одномерные системы автоматического управления
- •Линейные одномерные системы автоматического управления
- •Теория автоматического управления
- •Введение
- •Глава 1. Уравнения, элементарные блоки, структурные схемы и переходные процессы в сау
- •. Уравнения сау
- •1.2. Передаточные функции
- •1.3. Переходная и импульсная переходная функции. Показатели качества переходного процесса
- •1.4. Элементарные звенья
- •1.5. Структурные схемы сау и правила их преобразования
- •Глава 2. Обоснование метода передаточных функций для исследования сау
- •2.1. Преобразование Лапласа
- •2.2. Основные теоремы операционного исчисления
- •2.3. Реакция сау на произвольное входное воздействие. Интеграл Дюамеля
- •Глава 3. Частотные характеристики сау
- •3.1. Амплитудно-фазовые частотные характеристики
- •Логарифмические частотные характеристики
- •3.3. Частотные характеристики элементарных звеньев
- •Глава 4. Устойчивость сау
- •Алгебраический критерий устойчивости Гурвица.
- •4.2. Частотный критерий устойчивости Михайлова.
- •4.3. Частотный критерий устойчивости Найквиста
- •4.3.1. Критерий асимптотической устойчивости замкнутой системы, содержащей лишь устойчивые звенья
- •4.3.2. Применение критерия Найквиста к системам с нейтральными звеньями
- •4.3.3 Применение критерия Найквиста к системам с неустойчивыми звеньями
- •4.4 Метод d – разбиения
- •4.4.1 Линейная зависимость коэффициентов характеристического уравнения от одного параметра
- •4.4.2 Линейная зависимость коэффициентов характеристического уравнения от двух параметров
- •Приложение 1. Задачи
- •1. Динамические и частотные характеристики сау
- •Литература
Глава 2. Обоснование метода передаточных функций для исследования сау
В предыдущей главе
формальная замена операции дифференцирования
![]() степенью
степенью
![]() некоторого символа p
позволила ввести понятие передаточной
функции САУ, которая представляла собой
дробно рациональную функцию символа
p. В этой главе будут
даны обоснования такого формального
подхода и интерпретация передаточной
функции САУ. Кроме того на языке “MatLab”
приведены простые алгоритмы вычислений
переходной и импульсной переходной
функции САУ по ее передаточной функции.
некоторого символа p
позволила ввести понятие передаточной
функции САУ, которая представляла собой
дробно рациональную функцию символа
p. В этой главе будут
даны обоснования такого формального
подхода и интерпретация передаточной
функции САУ. Кроме того на языке “MatLab”
приведены простые алгоритмы вычислений
переходной и импульсной переходной
функции САУ по ее передаточной функции.
2.1. Преобразование Лапласа
Рассмотрим класс
функций
![]() таких,
что
таких,
что
|g(t)| gmax e t , gmax > 0 , > 0 , t [0, ) .
Эти функции
называются функциями экспоненциального
типа. В частности, ими служат экспонента,
тригонометрические функции, полиномиальные
дробно-рациональные функции, а также
суммы и произведения этих функций.
Поставим в соответствие
функцию
![]() комплексного переменного
комплексного переменного
![]() по
следующему правилу:
по
следующему правилу:
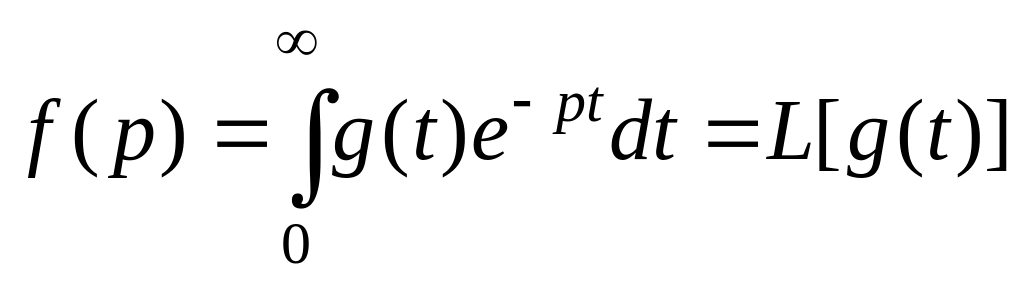 .
.
Интеграл существует
если
![]() ,
Функция
называется
преобразованием Лапласа функции
;
называют оригиналом, а
- изображением.
,
Функция
называется
преобразованием Лапласа функции
;
называют оригиналом, а
- изображением.
Обратное преобразование Лапласа определяется формулой
 ;
;
при этом полюсы функции лежат левее прямой интегрирования. Заметим что вычисление интеграла осуществляется при помощи теории вычетов [7].
Пусть
![]() а
а
![]() -
вещественные числа, тогда
-
вещественные числа, тогда
![]() - т.е. преобразование Лапласа определяет
линейный оператор.
- т.е. преобразование Лапласа определяет
линейный оператор.
Для вычисления изображений по Лапласу различных функции используется , а результаты сводятся в специальные таблицы [8,c.235]. Например,
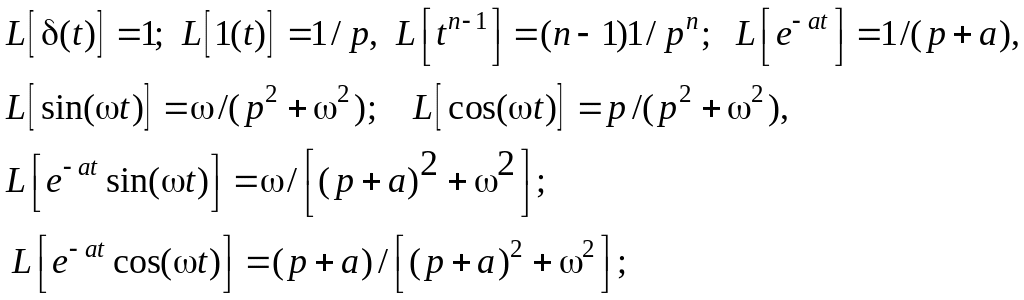
![]()
С помощью и правил интегрирования по частям находим
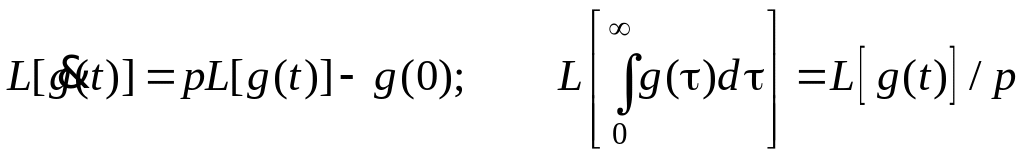 ;
;
![]()
Заметим, что все функции определены при t>0, а при равны нулю. Соотношения замечательны тем, что операции дифференцирования и интегрирования в области оригиналов сводятся в области изображений к алгебраическим операциям умножения и деления над полиномами от p.
Продемонстрируем метод решения дифференциальных уравнений с помощью преобразования Лапласа на примере следующего уравнения
![]()
Обозначим
![]() и найдем с помощью преобразование
Лапласа левой и правой частей уравнения
; В результате получим
и найдем с помощью преобразование
Лапласа левой и правой частей уравнения
; В результате получим
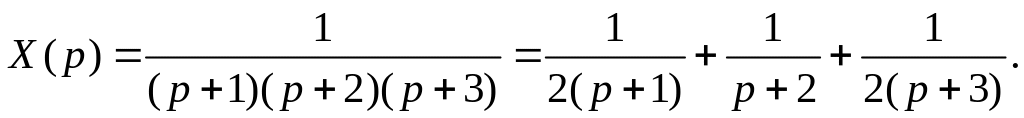
Обратное
преобразование Лапласа левой и правой
частей соотношения с учетом дает
решение исходного дифференциального
уравнения
![]()
2.2. Основные теоремы операционного исчисления
Докажем некоторые теоремы, результатами которых можно пользоваться для исследования свойств САУ.
Теорема о смещении.
Пусть
![]() и
и
![]() при
тогда
при
тогда
![]()
Доказательство. Пользуясь определением , запишем цепочку равенств
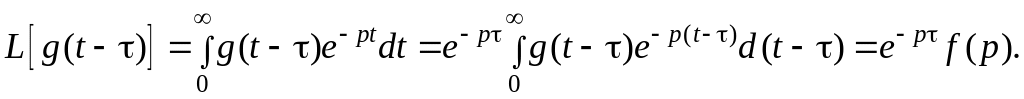
Теорема об
установившемся значении. Пусть
и
существует
![]() ;
тогда
;
тогда
![]() .
.
Доказательство:
Запишем изображение производной
![]() ,
пользуясь определением и формулами
,
,
пользуясь определением и формулами
,
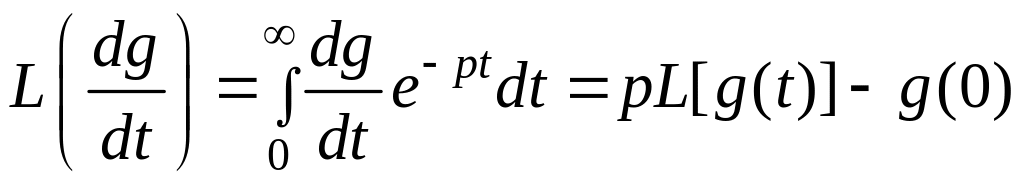 ;
;
откуда получаем
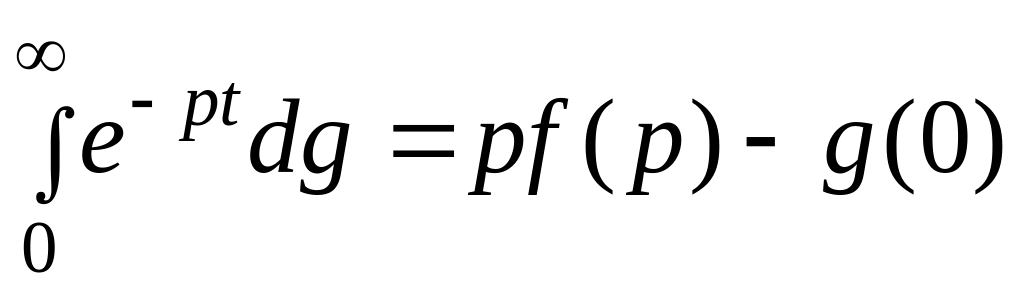 .
.
Перейдем в к
пределу при
![]() ,
в результате имеем
,
в результате имеем
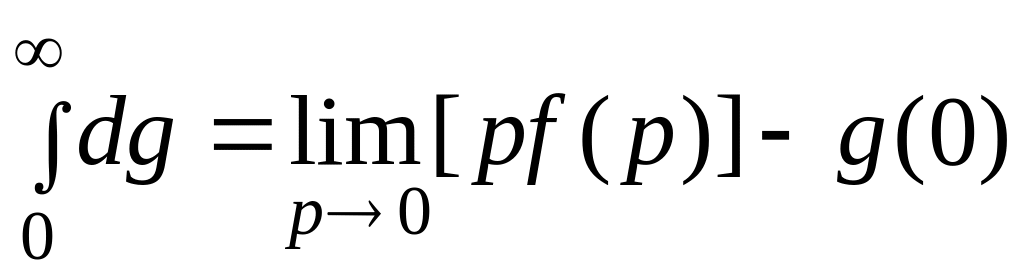 .
.
Поэтому
![]() .
.
Теорема о начальном
значении. Пусть
![]() ,
тогда
,
тогда
![]() .
.
Для доказательства
достаточно перейти в к пределу при
![]() .
.
Теорема о свертке
функций. Пусть
![]()
![]() и
и
![]() при
;
тогда
при
;
тогда
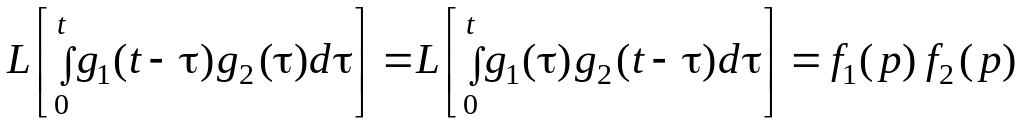 .
.
Интегралы в формуле
называются сверткой функций
![]() .
.
Упражнение 4.
Доказать теорему о свертке функций
воспользовавшись тем, что
![]() при
при
![]() .
.
Из следует, что умножению функций в области изображений соответствует свертка функций в области оригиналов. Этой формулой можно пользоваться для вычисления обратного преобразования Лапласа от произведения двух дробно-рациональных функций, если переписать ее в виде:
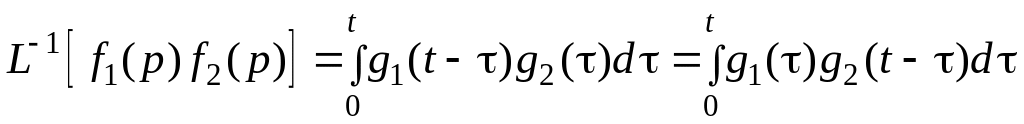 .
.
Для примера найдем
оригинал от произведения
 ,
воспользовавшись формулами (2.3), (2.12)
,
воспользовавшись формулами (2.3), (2.12)

