
- •3. Теорема додавання сумісних подій
- •7. Формула Бернуллі для обчислення ймовірності і наймовірнішого числа.
- •10.Умовна ймовірність та її властивості.
- •11.Формула Пуассона малоймовірних випадкових подій.
- •12. Довести формули повної імовірності та Байєса
- •Що називається подією, протилежною до даної. Коли кажуть, що з однієї випадкової події випливає інша.
- •15.Формули Байєса.
- •16. Наймовірніше число успіхів у схемі Бернуллі
15.Формули Байєса.
Ймовірності відомі до проведення досліду (так звані апріорні ймовірності). Як зміняться ймовірності гіпотез після проведення досліду? Тобто як обчислити ймовірності гіпотез
![]() ?
Відповідь на це питання дає теорема
гіпотез:
?
Відповідь на це питання дає теорема
гіпотез:
Ймовірності гіпотез після проведення досліду, тобто коли відбулася подія , обчислюються за формулою
=![]() (17)
(17)
Це формули Байєса.
Дійсно, за теоремою множення ймовірностей залежних подій маємо
![]() .
.
Звідки отримаємо формули (17). Ймовірності називаються апостеріорними, тобто такими, що змінилися після проведення досліду.
16. Наймовірніше число успіхів у схемі Бернуллі
Означення
1. Найімовірнішим
числом m0 появи
події А в n незалежних
випробовуваннях називається число, для
якого ймовірність ![]() не
менша ймовірності кожного з решти
можливих варіантів, тобто
не
менша ймовірності кожного з решти
можливих варіантів, тобто
![]()
![]() .
.
Якщо найімовірніше
число ![]() ,
то повинні виконуватись такі умови:
,
то повинні виконуватись такі умови:
![]() . (1)
. (1)
![]() . (2)
. (2)
З нерівності (1) отримується:
![]()
звідки (після скорочень)
![]()
Розв’язуючи нерівність відносно , отримують:
![]() . (3)
. (3)
Аналогічно з нерівності (2) отримується:
Звідки
; . (4)
Остаточно отримується нерівність:
. (5)
Зауваження. Довжина інтервалу, що визначається нерівністю (5), рівна одиниці:
тому, коли межі інтервалів є дробові числа, то отримується одне значення наймовірнішого числа , якщо ж межі є цілими числами, то отримується два значення наймовірнішого числа успіхів
17.Функція
розподілуУніверсальним
способом задання закону розподілу
ймовірностей є функція
розподілу
![]() Цю
функцію можна тлумачити так:унаслідок
експерименту випадкова величина може
набути значення,меншого за х.
Для дискретних величин
Цю
функцію можна тлумачити так:унаслідок
експерименту випадкова величина може
набути значення,меншого за х.
Для дискретних величин
![]()
Функція
розподілу — неспадна, неперервна зліва,
![]()
![]()
Для довільних
![]()
![]()
Якщо Х
— неперервна випадкова величина, то
![]() — неперервна і диференційована; її
похідна
— неперервна і диференційована; її
похідна
![]() називається щільністю
розподілу ймовірностей.
При цьому
називається щільністю
розподілу ймовірностей.
При цьому
![]() — невід’ємна функція, для якої
— невід’ємна функція, для якої
![]()
![]()
![]()
Властивості:
1.0F(x)1
2.F(x) є неспадною функцією,а саме F(x2)F(x1), якщо х2х1
18.
19.Окремо на листках
20,21,23.Математичним
сподіванням,
або середнім значенням, МХ
випадкової величини, називається ряд
![]() (для дискретних випадкових величин) і
інтеграл
(для дискретних випадкових величин) і
інтеграл
![]() (для неперервних випадкових величин),
якщо вони абсолютно збіжні. Математичне
сподівання має такі властивості:
(для неперервних випадкових величин),
якщо вони абсолютно збіжні. Математичне
сподівання має такі властивості:
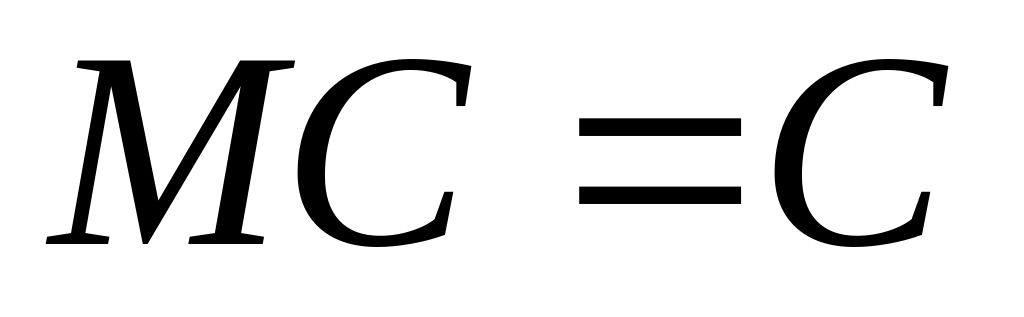 (С
— стала);
(С
— стала);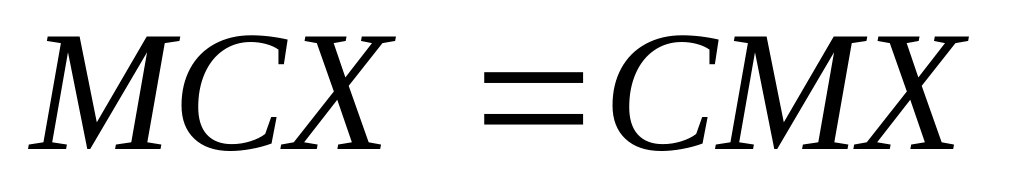 ;
;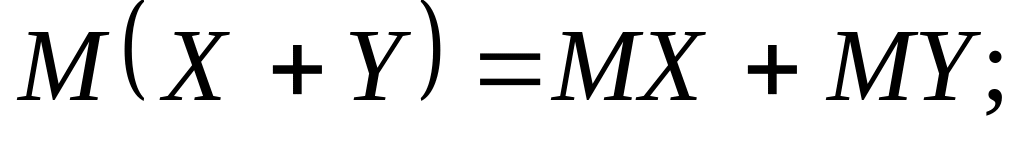
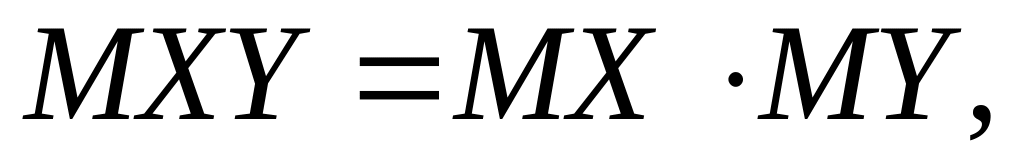 якщо Х
і Y
— незалежні випадкові величини.
якщо Х
і Y
— незалежні випадкові величини.
Початковий, центральний і абсолютний початковий моменти порядку k величини Х визначають відповідно за такими формулами:
![]()
![]()
Якщо існує початковий абсолютний момент порядку k, то існують усі моменти нижчих порядків.
Медіаною
![]() випадкової величини є Х
будь-який корінь рівняння
випадкової величини є Х
будь-який корінь рівняння
![]()
Мода дискретної величини
![]() — це таке її значення, імовірність якого
найбільша.
— це таке її значення, імовірність якого
найбільша.
Модою неперервного розподілу є значення випадкової величини, за якого щільність розподілу має максимум.
Асиметрія
випадкової величини визначається за
формулою:![]()
Ексцес
випадкової величини обчислюють за
формулою:
![]()
22.Дисперсія
(позначається через
![]() )
випадкової величини Х
визначається за формулою:
)
випадкової величини Х
визначається за формулою:
![]()
Основні властивості дисперсії:
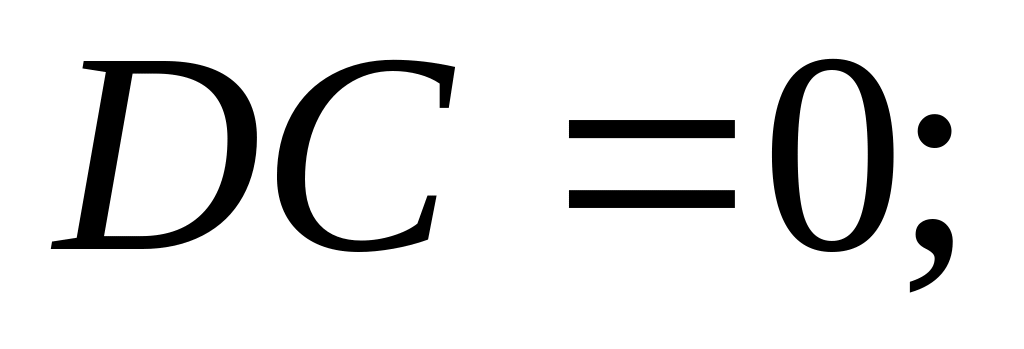
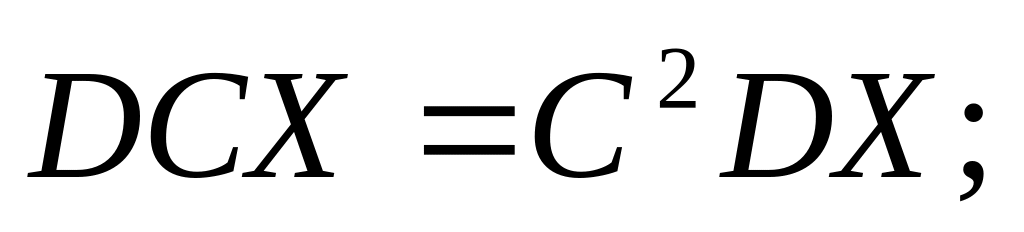
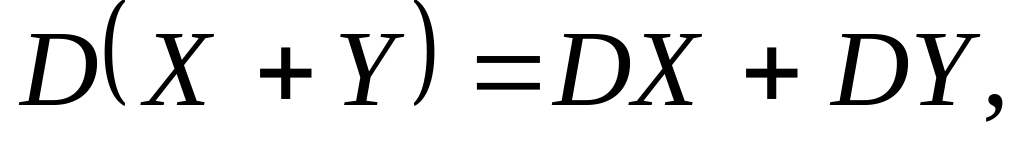 якщо випадкові величини незалежні.
якщо випадкові величини незалежні.
Середнє квадратичне відхилення (позначається літерою ) є квадратним коренем із дисперсії.
Якщо від випадкової величини віднімемо її математичне сподівання, то дістанемо центровану випадкову величину, математичне сподівання якої дорівнює нулю. Ділення випадкової величини на її середнє квадратичне відхилення називається нормуванням цієї випадкової величини.
Випадкова величина
![]() має нульове математичне сподівання й
одиничну дисперсію.
має нульове математичне сподівання й
одиничну дисперсію.
25. Математичне сподівання.
Випадкова величина може приймати різні числові значення, тому практично важливим є середнє значення випадкової величини. Для оцінки середнього (у ймовірнісному сенсі) значення випадкової величини вводиться поняття математичного сподівання, яке є дійсним середнім значенням випадкової величини і визначається з врахуванням різних ймовірностей її окремих значень.
Математичне сподівання випадкової
величини
![]() позначаємо
позначаємо
![]() .
Для дискретної випадкової величини
,
заданої рядом розподілу
.
Для дискретної випадкової величини
,
заданої рядом розподілу
-
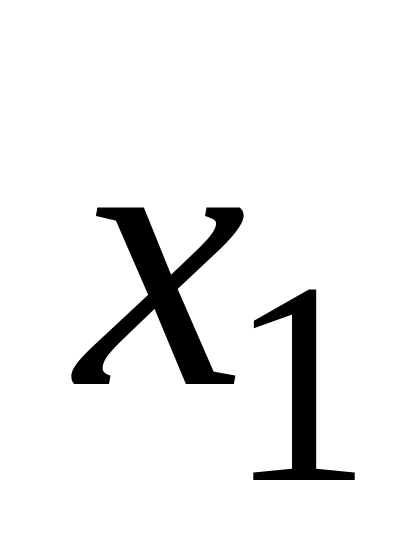
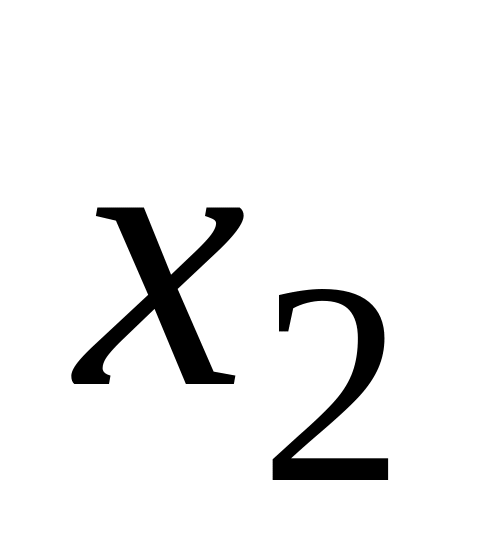
…

…
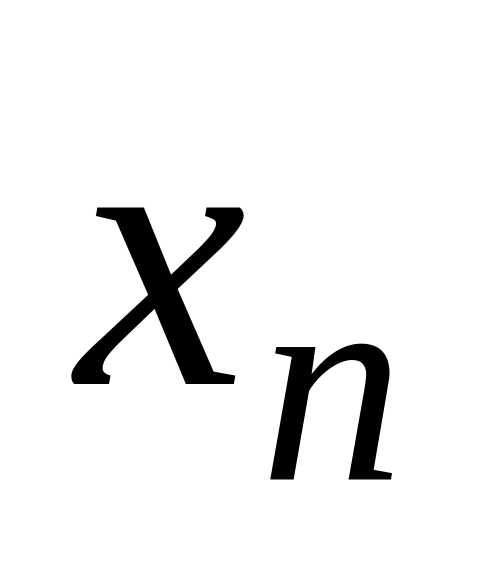
…
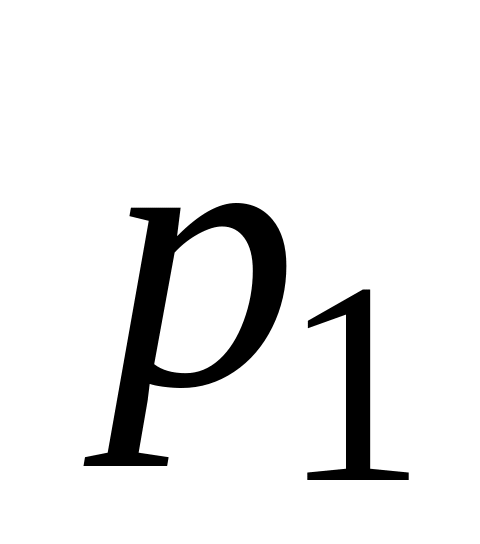
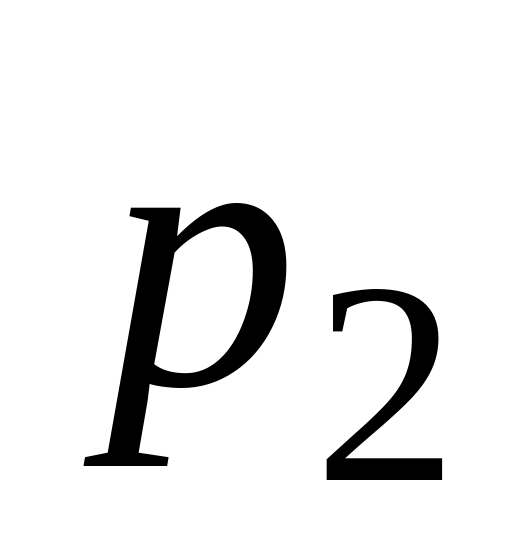
…

…
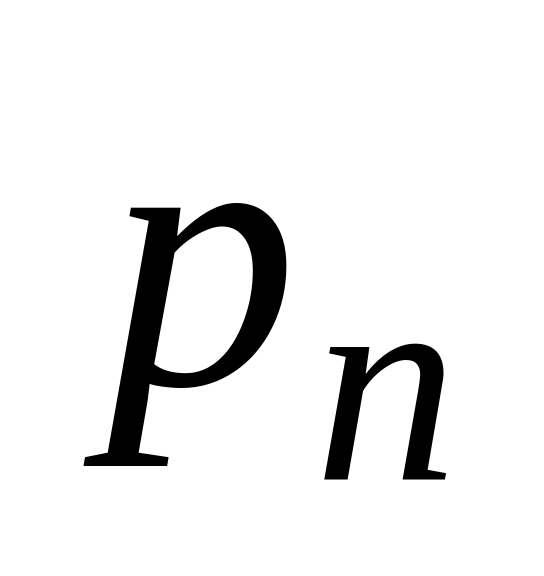
…
де
![]() ,
математичне сподівання обчислюється
за формулою
,
математичне сподівання обчислюється
за формулою
=![]()
![]() ,
(1)
,
(1)
якщо ряд справа збігається.
Нехай
- неперервна випадкова величина, значення
якої
![]() ,
і
,
і
![]() - її щільність розподілу. Розіб’ємо
відрізок
- її щільність розподілу. Розіб’ємо
відрізок
![]() на
на
![]() частин, довжини яких
частин, довжини яких
![]() ,
,
![]() ,…,
,…,![]() .
Візьмемо в кожному частинному відрізку
.
Візьмемо в кожному частинному відрізку
![]() точку
точку
![]() .
Добуток
.
Добуток
![]() приблизно дорівнює ймовірності попадання
неперервної випадкової величини в
інтервал
приблизно дорівнює ймовірності попадання
неперервної випадкової величини в
інтервал
![]() ,
а сума
,
а сума
![]() наближено дорівнює математичному
сподіванню неперервної випадкової
величини. Якщо існує границя
наближено дорівнює математичному
сподіванню неперервної випадкової
величини. Якщо існує границя
![]() ,
то вона називається математичним
сподіванням неперервної випадкової
величини і позначається
=
,
то вона називається математичним
сподіванням неперервної випадкової
величини і позначається
=![]() .
(2)
.
(2)
У
випадку, якщо
![]() ,
то
=
,
то
=![]() ,
причому інтеграл повинен збігатися
абсолютно. Відзначимо найпростіші
властивості математичного сподівання:
,
причому інтеграл повинен збігатися
абсолютно. Відзначимо найпростіші
властивості математичного сподівання:
.
![]() ;
де
;
де
![]() - стала величина,
- стала величина,
.
![]()
![]() ;
;
.
![]()
![]() +
+![]() ;
;
![]() .
.
![]() ;
якщо випадкові величини
;
якщо випадкові величини
![]() незалежні.
незалежні.
Дві випадкові величини називаються незалежними, якщо закон розподілу однієї з них не залежить від того, які можливі значення прийняла інша випадкова величина.
Математичне сподівання називають
центром розподілу ймовірностей випадкової
величини
,
випадкова величина
![]() називається центрованою.
називається центрованою.
24. Дисперсія.
Для
характеристики розсіювання значень
випадкової величини відносно її центра
розподілу (математичного сподівання)
вводять числову характеристику –
дисперсію випадкової величини.
Позначається
![]() .
За означенням, дисперсією випадкової
величини
називається математичне сподівання
квадрату відхилення випадкової величини
від її математичного сподівання
.
За означенням, дисперсією випадкової
величини
називається математичне сподівання
квадрату відхилення випадкової величини
від її математичного сподівання
=![]() .
(3)
.
(3)
Дисперсія обчислюється за формулами
![]() =
=![]() (4)
(4)
для дискретних випадкових величин, і
=![]() (5)
(5)
для неперервних випадкових величин.
Тут для простоти позначено
![]() =
.
=
.
Найпростіші властивості:
.
![]() ;
де
- стала величина,
;
де
- стала величина,
.
![]()
![]() ;
;
.
![]()
![]() +
+![]() ;
якщо випадкові величини
незалежні.
;
якщо випадкові величини
незалежні.
Практично дисперсію обчислюють за робочою формулою
=![]()
![]() ,
(6)
,
(6)
де
![]()
![]() для дискретних випадкових величин і
для дискретних випадкових величин і
![]() для неперервних випадкових величин.
для неперервних випадкових величин.
Дисперсія є кількісною оцінкою відхилення
випадкової величини від її математичного
сподівання. Проте, оскільки дисперсія
має розмірність квадрата випадкової
величини, то для оцінки міри розсіювання
використовують характеристику
![]() ,
яка називається середнім квадратичним
або стандартним відхиленням випадкової
величини. Оскільки
,
яка називається середнім квадратичним
або стандартним відхиленням випадкової
величини. Оскільки
![]() ,
то і
,
то і
. Розмірність середнього квадратичного відхилення співпадає з розмірністю випадкової величини.
