
- •1 Направления искусственного интеллекта и понятие иис – 2 ч. [1; 2; 9]
- •1.1 Основные направления искусственного интеллекта и их характеристика. (Гаврилова)
- •1.1.1 Основные направления искусственного интеллекта и их характеристика. (Андрейчикова)
- •1.2 Состояние работ в области экспертных систем и направлениям искусственного интеллекта. (Попов)
- •1.3 Понятие интеллектуальной информационной системы (иис). (Андрейчикова)
- •1.5 Классификация иис. (Андрейчикова)
- •2 Понятие экспертных систем. – 2 ч. [1; 2; 3; 9]
- •2.1 2.2 2.3 Экспертные системы (эс). Назначение экспертных систем. Формальные основы экспертных систем. (Попов)
- •Назначение экспертных систем
- •Формальные основы экспертных систем
- •3 Архитектура экспертных систем и этапы разработки - 2 ч. [2; 8; 9]
- •3.3 Этапы разработки экспертных систем. (Попов)
- •5 Методы и модели представления знаний. (Попов)
- •5.1 Формальная логическая модель представления знаний. (Попов)
- •5.2. Семантическая модель представления знаний. (Попов)
- •5.3 Фреймовая модель представления знаний. (Попов)
- •5.4 Продукционная модель представления знаний. (Попов)
- •5.6 Модель представления знаний: “прецеденты”.
- •5.5 Модель доски объявлений для представления знаний.
- •5.7 Гибридные модели представления знаний
- •6 Методы поиска решений в эс
- •7 Понятие и определение нечетких знаний – 2 ч. [3; 14]
- •7.1 Нечеткие знания
- •7.2 Понятие лингвистической переменной, определение ее значения
- •7.3 Понятие нечеткого множества
- •7.4 Определение нечеткого множества (через базовую шкалу и функцию принадлежности)
- •7.5 Понятие функции принадлежности
- •7.6 Операции с нечеткими знаниями
- •8 Стратегии получения знаний - 2 ч. [3]
- •8.1 Извлечение знаний из данных, приобретение знаний, формирование знаний. Теоретические аспекты извлечения знаний.
- •Теоретические аспекты извлечения знаний
- •Психологический аспект извлечения знаний
- •Лингвистический аспект извлечения знаний
- •Гносеологический аспект извлечения знаний
- •Теоретические аспекты структурирования знаний
- •Историческая справка
- •Иерархический подход
- •Традиционные методологии структурирования
- •Объектно-структурный подход (осп)
- •9 Проектирование экспертных систем - 2ч. [1; 3]
- •9.1 Этапы проектирования экспертной системы: идентификация, концептуализация, формализация, реализация, тестирование, опытная эксплуатация.
- •9.4 Технология проектирования и разработки промышленных эс.
- •9.5 Характеристика этапов разработки эс.
- •9.6 Технология быстрого прототипирования эс.
- •9.7 Характеристика стадий разработки прототипа эс.
- •10 Понятие нейроинформатики, история развития
- •Задача обучения нейронной сети на примерах.
- •12.1 Интерфейс вывода нейросетевого блока
- •12.2 Интерпретатор нейросетевого блока
- •12.3 Блок «Учитель» нейроимитатора
- •12.4 Блок «Оценка»
- •4.3.8. Конструктор нейронной сети
- •12.7 Блок «Констрастер»
- •4.3.9. Контрастер нейронной сети
- •42. Схема работы интеллектуального компонента прогнозирования временных рядов показателей.
- •44. Персептрон Розенблатта.
- •46.Карта самоорганизации Кохонена.
- •45 Многослойный перцептрон и его обучение
12.3 Блок «Учитель» нейроимитатора
НС обучается с учителем, если присутствуют выходные параметры. В рез-те работы блока учитель формир-ся ф-ция регрессии.
При создании новой НС в памяти отводится место под массив синаптических весов. Перед началом обучения этот массив заполняется случ-ми числами в нормиров-ом диапазоне. Этот массив наз-ся синаптической картой. В нач. момент времени на входные нейроны через вход синапсы подается вектор вх. сигналов. Далее этот сигнал распро-ся по всем связям м/у нейронами, изменяясь при прохождении через каждый нейрон. В рез-те сигнал поступает на выход. Т.к. НС обуч-ся с учителем, мы имеем необходимый выходной параметр, с которым и сравниваем полученный случ-й У. (Вся процедура однократного прохождения сигналов по НС наз-ся тактом функц-я). Задача блока Учитель состоит в проведении сравнения и по результатам оценки модификации соответствующих коэффициентов, используя методы оптимизации. Пример сети, обуч-ой с уч-лем – перцептрон.
Рассмотрим следующий компонент искусственной нейронной сети - учитель в режимах обучения и дообучения. Существует ряд алгоритмов обучения, жестко привязанных к архитектуре нейронной сети. Примерами таких алгоритмов могут служить обучение (формирование синаптической карты) сети Хопфилда, обучение сети Кохонена и ряд других аналогичных сетей. Методы обучения нейронных сетей типа карт Кохонена представлены в [92,93,233,2.
Рассмотрим особенности алгоритмов обучения многослойных сетей, которые применяются в настоящей разработке. Минимизация функции оценки выполняется с привлечением градиентных методов оптимизации. Изучению градиентных методов обучения нейронных сетей посвящены [11,40,41,113,200,210,230]. Все градиентные методы объединены использованием градиента как основы для вычисления направления спуска. Для разработанного нейроимитатора применяются следующие методы: метод наискорейшего спуска, модифицированный Parian, квазиньютоновский [40].
Метод наискорейшего спуска работает, как правило, на порядок быстрее методов случайного поиска [110], Как правило, этот метод позволяет за несколько циклов обучения с последующим случайным изменением параметров найти глобальный минимум. Серьезным недостатком метода наискорейшего спуска является его чувствительность к форме окрестности минимума. Легко показать, что для точного достижения минимума потребуется бесконечное число шагов метода градиентного спуска. Этот эффект получил название овражного, а методы оптимизации, позволяющие бороться с этим эффектом - антиовражных.
Одним из простейших антиовражных методов является метод kРаrТаn[40,110].
Существует большое семейство квазиньютоновских методов, позволяющих на каждом шагу проводить минимизацию в направлении минимума квадратичной формы. Одним из наиболее часто используемых методов из семейства одношаговых квазиньютоновоских методов является BFGS метод. Этот метод хорошо зарекомендовал себя при обучении нейронных сетей, применяющихся в информационных системах предприятий.
Все алгоритмы обучения сетей методом обратного распространения ошибки опираются на способность сети вычислять градиент функции ошибки по обучающим параметрам [110]. Таким образом, акт обучения состоит из вычисления градиента и собственно обучения сети (модификации параметров сети). Однако существует множество неградиентных методов обучения, таких, как метод покоординатного спуска, метод случайного поиска и целое семейство методов Монте-Карло. Все эти методы могут использоваться при обучении нейронных сетей, хотя, как правило, они менее эффективны, чем градиентные методы. К числу не градиентных методов обучения можно отнести следующие: метод случайной стрельбы (представитель семейства методов Монте-Карло), метод покоординатного спуска (псевдоградиентный метод), метод случайного поиска (псевдоградиентный метод), метод Нелдера-Мида [110].
Методы обучения нейронных сетей типа карт Кохонена представлены в [92,93,233,234].
При обучении сети градиентными методами в качестве стандартной оценки работы нейросети (функции ошибки) выступает оценка по методу наименьших квадратов (МНК) [40,41]:
 (4.9)
(4.9)
где Н - оценка работы нейросети;
![]() - значение р-й
компоненты вектора выходного сигнала
нейросети;
- значение р-й
компоненты вектора выходного сигнала
нейросети;
Уsр - требуемое значение; S - число примеров;
Р - размерность вектора у.
В [40,41,110] отмечается, что процесс обучения нейросети можно значительно ускорить, если вместо оценки (4.9) применять более специализированные. Они строятся путем формализации требований к нейросетевому решателю для конкретного вида задач. Для задач perрессии более подходящей является оценка МНК с допуском [110]:
при
![]()
![]() при
при
![]() (4.10)
(4.10)
при
![]()
где
![]() - допуск или допустимая погрешность;
- допуск или допустимая погрешность;
![]()
![]() - требуемое значение сигнала;
- требуемое значение сигнала;
![]() -
ответ сети; так как
если целевое значение
измерено с погрешностью
ε,
то достаточно, если выданный сетью ответ
попадет в интервал
[
-ε,
+ε].
При достижении этого результата пример
считается
решенным. Оценка вида (4.10) позволяет
ускорить процесс обучения и получить
более сглаженные нейросетевые функции,
так как тогда требования
к сложности нейросети выражаются не в
виде оценки константы
Липшица [41,110] (4.5), а в виде (4.6), т.е.
становятся более мягкими.
Сглаженная функция, в свою очередь,
обладает более высокими экстраполяционными
и интерполяционными способностями
[199].
-
ответ сети; так как
если целевое значение
измерено с погрешностью
ε,
то достаточно, если выданный сетью ответ
попадет в интервал
[
-ε,
+ε].
При достижении этого результата пример
считается
решенным. Оценка вида (4.10) позволяет
ускорить процесс обучения и получить
более сглаженные нейросетевые функции,
так как тогда требования
к сложности нейросети выражаются не в
виде оценки константы
Липшица [41,110] (4.5), а в виде (4.6), т.е.
становятся более мягкими.
Сглаженная функция, в свою очередь,
обладает более высокими экстраполяционными
и интерполяционными способностями
[199].
Для задач классификации целевая переменная является дискретной (номинальной). Ее кодирование проводится в соответствие с (4.4), т.е. сеть будет иметь несколько выходных полей, каждому из которых соответствует определенный класс. Тогда ответом нейросети на предъявленный пример будет считаться номер класса, соответствующий номеру выходного параметра, на котором зафиксировано наибольшее значение сигнала (интерпретатор «победитель забирает все» [41]). В этом случае в качестве оценки работы нейросети предпочтительнее использовать оценку вида «расстояние до множества правильных ответов», предложенную в [41]:
![]() (4.11)
(4.11)
где k - номер «истинного» класса;
α, - выходные сигналы сети;
i=l...Р, Р - число выходных сигналов,
ε -требуемый уровень отличия «истинного» сигнала от остальных;
ρ - функция расстояния до множества правильных ответов.

(4.10)
Где β0=αk-ε;
βφ=αl - текущие выходные сигналы (за исключением αk), переобозначенные таким образом, что βφ>βφ+1;
j=l..P-l, Р-число выходных сигналов;
l - максимальный номер, такой, что верно неравенство
 ,
при l<Р-1,
или равенство l=Р-1.
,
при l<Р-1,
или равенство l=Р-1.
Настройка параметров нейросети. Задание функции ошибки определенного вида позволяет вычислить для каждого примера обучающей выборки оценку работы нейросети и определить направление изменения ее параметров для уменьшения значения оценки Н. Процесс итерационного изменения параметров нейросетевой функции называется обучением [40,41].
В![]() ыбор
нейросетевого решателя в виде функции
(4.2) позволяет
применить
градиентные методы оптимизации для
поиска такого вектора параметров
а*,
который доставляет минимум выбранному
функционалу
ошибки, т.е. выполняется условие .
ыбор
нейросетевого решателя в виде функции
(4.2) позволяет
применить
градиентные методы оптимизации для
поиска такого вектора параметров
а*,
который доставляет минимум выбранному
функционалу
ошибки, т.е. выполняется условие .
Д![]() ля
этого вычисляются
значения для каждого аi.
При использовании стандартной оценки
МНК по всей выборке (4.9), имеем
ля
этого вычисляются
значения для каждого аi.
При использовании стандартной оценки
МНК по всей выборке (4.9), имеем
(4.13)![]()
![]()
(4.14)
где S — число примеров в обучающей выборке;
s - номер примера;
Hs - оценка для s-гo примера.
В![]() ычисление
основано
на формуле дифференцирования сложной
функции:
ычисление
основано
на формуле дифференцирования сложной
функции:
,
(4.15)![]()
В соответствии с (4.2), (4.14) для выходного (k+1-го) слоя:
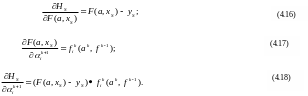
М![]()
![]() ы
получили формулу для вычисления
производной по параметрам
выходного слоя. Чтобы найти
для слоя, посылающего сигналы
выходному слою нейронной сети, выразим
ы
получили формулу для вычисления
производной по параметрам
выходного слоя. Чтобы найти
для слоя, посылающего сигналы
выходному слою нейронной сети, выразим
![]() (4.19)
(4.19)
Т
(4.20)
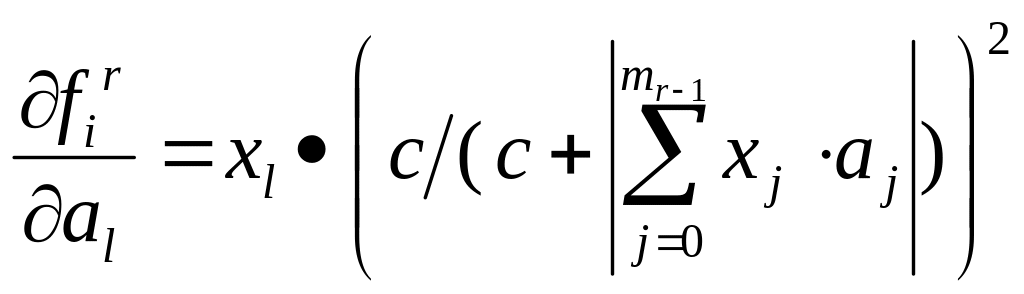
Г
(4.21)
На основе формул (4.18 - 4.21) можно рекурсивно вычислит производные по всем настраиваемым параметрам сети, что позволяет использовать тот или иной градиентный метод оптимизации, например
метод наискорейшего спуска [40], который заключается в итерационном изменении параметров в соответствии с правилом:
![]() (4.22)
(4.22)
где t - номер итерации;
h - шаг оптимизации.
Величина шага вычисляется на каждой итерации путем одномерной оптимизации функции H(ai,h,) при фиксированных а;.
На практике метод (4.22) часто оказывается малоэффективным по сравнению с методами квадратичной численной оптимизации в связи со сложным рельефом функции Н. Из теории квадратичной оптимизации известно, что метод Ньютона позволяет найти минимум квадратичной формы за один шаг. Однако поиск обратной матрицы вторых производных для всех параметров нейросети требует слишком больших вычислительных затрат, кроме этого она может не быть положительно определена, поэтому применяют методы, использующие аппроксимацию вторых производных Н по параметрам а, например BFGS-метод [41]. Известным методом этого класса является метод сопряженных градиентов [41,230]. Несмотря на то, что функция Н в общем случае не является квадратичной, метод сопряженных градиентов работает достаточно эффективно [230]. В качестве правила изменения параметров нейросети в этом случае выбирается:
![]() (4.23)
(4.23)
где d,(t) - направление оптимизации;
h - шаг оптимизации.
В соответствии с [230], одной из эффективных формул, определяющих направление dj(t), является формула Полака - Рибера (Polak -Ribiere):
(4.24)
![]()
где

(4.25)![]()
На основе приведенных формул строится алгоритм градиентной оптимизации параметров нейросети:
Инициализация массива настраиваемых параметров a некоторыми равномерно распределенными в интервале [-0.01, 0.01] случайными величинами.
Вычисление F(a,x) для очередного примера задачника.
Вычисление Н для примера в соответствии с выбранным из (4.9-4.11) видом оценки.
4. Вычисление
![]()
![]() - для текущего примера по формулам
- для текущего примера по формулам
(4 18-4.21), накопление суммарного градиента.
Если обработаны не все примеры, перейти к п.2.
Выбор направления оптимизации в соответствии с методом (4.22) или (4.23-4.25).
Одномерная оптимизация шага градиентного спуска h в вы бранном направлении.
Изменение параметров а.
Вычисление Н.
Если (Н>Нmin ) и (|| ||>0), то перейти к п.2, иначе – конец обучения.
При изменении параметров нейросети необходимо контролировать их значение, чтобы избежать затруднений в обучении. В случае использования функции (4.3) в качестве функции активации, диапазон наиболее аффективных значений параметров а — интервал [-1,1} [41]-Для удержания значений а в данном диапазоне применяют проективный метод контроля
 а, -1<a<1,
а, -1<a<1,
a= a-1, a<-1, (4.26)
1, а> 1,
Общей проблемой методов локальной оптимизации, к которым относятся градиентные методы, является остановка в локальных минимумах, далеких от оптимального решения. Локальный минимум характеризуется условиями: (Н>Нmin ) и (|| ||=0), В этом случае применяется сдвиг значений параметров нейросети в случайном направлении: а = а + ξ, где ξ - равномерно распределенная на интервале [ξmin,ξmax] случайная величина. Задание значений ξmin,ξmax определяет степень изменения параметров нейросети. Интервал может постепенно увеличиваться, если изменения не приводят к выходу из локального минимума.
Оценка и коррекция нейросетевой модели
Дня оценки качества полученной модели используется оценка работы нейросети на тестовой выборке, или ошибка обобщения. Она характеризует способность ИНС обрабатывать новые данные в отличие от ошибки обучения, которая отражает качество настройки нейросети на конкретные примеры. Наиболее распространенным методом оценки моделей является метод перекрестного оценивания [252].
В случае, если ошибка сети превышает допустимую, необходимо вернуться на предыдущие этапы построения модели и изменить некоторые параметры нейросети.
Первым этапом коррекции модели является генерация нескольких экземпляров нейросети и их обучение, т.к. результаты обучения зависят от начальных значений весов синапсов, которые генерируются для каждой сети случайным образом. После обучения нескольких экземпляров выбирается сеть С минимальной тестовой ошибкой. Различные нейросети могут ошибаться на различных примерах тестовой выборки. В этом случае можно сформировать комитет из нейросетей и вычислять окончательный ответ по задаче как среднее арифметическое ответов отдельных сетей. В этом случае средняя ошибка комитета будет меньше средней ошибки каждой нейросети [57]. Изменение вида или параметров функции оценки также может улучшить качество работы ИНС. В [41] предлагается следующая методика обучения сетей с оценкой МНК с допуском: устанавливается максимальное значение допуска, сеть обучается, затем величина допуска постепенно снижается с дообучением сети, пока оценка не достигнет требуемого уровня.
Если нейронная сеть заданной структуры не может удовлетворительно решить задачу, возможно несколько вариантов действий:
Добавление новых нейронов, новых слоев.
Увеличение значения характеристики крутизны функции (4.3).
Уменьшение значения характеристики крутизны функции (4.3).
Первые два варианта исходят из предположения, что модель не достаточно сложна или имеет недостаточную величину константы Липшица (4.5) для освоения задачи. Третий вариант предполагает что нейросетевая функция недостаточно 1ладка для удовлетворительной аппроксимации. Уменьшение характеристики приведет к сглаживанию функции (4.3).
Для повышения качества модели могут быть использованы различные методы предобработки данных. например; сглаживание и фильтрация, кодирование количественного признака как дискретного изменение состава обучающей выборки, изменение состава параметров. описывающих исследуемый объект. В настоящее время процесс коррекции нейросетевых моделей носит эвристический характер ц основан на знаниях эксперта о конкретной задаче предметной области.
