
- •1.Векторная функция скалярного аргумента
- •2. Кривые в пространстве, длина кривой.
- •3.Две леммы о векторной функции скалярного аргумента.
- •4.Сопровождающий трехгранник кривой.
- •5.Соприкасающаяся окружность. Кривизна и кручение кривой.
- •6. Формулы Френе.
- •7. Вычисление кривизны и кручения
- •1. Натуральная параметризация.
- •2. Произвольная параметризация.
- •Касательная плоскость и нормаль к поверхности
- •Уравнение касательной плоскости имеет вид
- •9. Первая квадратичная форма поверхности
- •Площадь поверхности.
- •10.Криволинейные системы координат.
- •2) Сферическая система координат.
- •11.Дифференцирование скалярного поля.
- •12.Дифференцирование векторного поля.
- •13)Оператор Гамильтона. Дифференцирование произведений.
- •14.Дифференциальные операции второго порядка над полями.
- •15)Поверхностный интеграл первого рода.
- •21.Инвариантное определение операций div, grad, rot…
- •28.Ряды Фурье по общим ортогональным системам.
- •30.Замкнутость и полнота ортогональных систем функций. Замкнутость тригонометрической системы.
- •32.Интегральная формула Фурье.
1.Векторная функция скалярного аргумента
Векторные функции скалярного аргумента. Предел, непрерывность, производная и интеграл Римана вектор-функции.
Будем рассматривать трёхмерное
Евклидово пространство
 ,
т.е. пространство, в котором определена
операция скалярного произведения.
Говорят, что в
задана векторная функция
,
т.е. пространство, в котором определена
операция скалярного произведения.
Говорят, что в
задана векторная функция
 ,
определённая на множестве
,
определённая на множестве
 ,
если для каждого
,
если для каждого
 ставится в соответствие
ставится в соответствие
 (причём
(причём
 -
одномерное множество).
-
одномерное множество).
Рассмотрим случай, когда
 -отрезок.
В
введём ортонормированный базис
-отрезок.
В
введём ортонормированный базис
 .
Тогда вектор
можно разложить по данному базису:
.
Тогда вектор
можно разложить по данному базису:
 ,
где
,
где
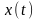 ,
,
 ,
,
 - проекции вектора на соответствующие
орты.
- проекции вектора на соответствующие
орты.
 назовем пределом векторной функции
в точке
назовем пределом векторной функции
в точке
 ,
если
,
если
 (1). Так как под знаком предела стоит
модуль, то это скалярная величина.
Обозначим этот предел как
(1). Так как под знаком предела стоит
модуль, то это скалярная величина.
Обозначим этот предел как
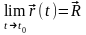 .
(но подразумевать под этим выражением
будем выражение (1)). Если
.
(но подразумевать под этим выражением
будем выражение (1)). Если
 ,
то можно доказать следующее утверждение:
,
то можно доказать следующее утверждение:
Теорема 1:
является пределом функции
в
точке
 тогда и только тогда , когда
тогда и только тогда , когда
 ,
,
 ,
,
 .
Доказательство.
.
Доказательство.
Непосредственно из опр. имеем:
 .
Очевидно, что правая часть равенства
(2) стремиться к 0, так как
.
Очевидно, что правая часть равенства
(2) стремиться к 0, так как
 ,
,
 ,
,
 при
при
 .
Так как каждая из скобок стремиться к
0, то и левая часть равенства (1) стремиться
к 0, что и требовалось доказать.
.
Так как каждая из скобок стремиться к
0, то и левая часть равенства (1) стремиться
к 0, что и требовалось доказать.
В екторная
функция
называется непрерывной в точке
,
если
екторная
функция
называется непрерывной в точке
,
если
 .
.
Векторная функция
называется непрерывной на отрезке
 ,
если она непрерывна в каждой точке
отрезка.
,
если она непрерывна в каждой точке
отрезка.
Из непрерывности функции следует непрерывность её компонентов , , и наоборот.
Производной векторной функции в точке t называется:
 .
Производная обозначается несколькими
эквивалентными способами:
.
Производная обозначается несколькими
эквивалентными способами:
 ,
,
 .
Вторая производная определяется как
производная от первой
.
Вторая производная определяется как
производная от первой
 .
.
Выберем точку и отложим от неё множество векторов (см. рис. 1). Кривая, которую образуют концы векторов, называется годографом.
Р ассмотрим
более подробно два соседних вектора и
их разность (см. рис. 2). Очевидно, что
вектор
ассмотрим
более подробно два соседних вектора и
их разность (см. рис. 2). Очевидно, что
вектор
 при
при
 начинает скользить по годографу. То
есть геометрическим смыслом производной
является вектор, лежащий на касательной
к годографу.
начинает скользить по годографу. То
есть геометрическим смыслом производной
является вектор, лежащий на касательной
к годографу.
Для того, что бы функция была дифференцируема,
необходимо выполнение равенства : ,
,
где
 .
.
Свойства производной.
1.
 .
.
2.
 .
.
3.
 .
.
4.
 .
.
5.
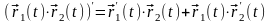 .
.
6.
 .
.
Теорема 2: Если ,
то вектор
перпендикулярен
вектору
.
,
то вектор
перпендикулярен
вектору
.
Доказательство. Из условия теоремы
имеем:
 .
Продифференцировав это равенство,
получим:
.
Продифференцировав это равенство,
получим:
 ,
что и требовалось доказать.
,
что и требовалось доказать.
Используя равенство
 ,
можно разложить векторную функцию
,
можно разложить векторную функцию
 в ряд Тейлора:
в ряд Тейлора:
 .
.
2. Кривые в пространстве, длина кривой.
Понятие прямая так же как и понятие
точки первичны и не определяются.
Рассмотрим отображение некоторой точки
 в трехмерное пространство и обозначим
его
в трехмерное пространство и обозначим
его
 .
Будем говорить, что отображение
непрерывно, если
.
Будем говорить, что отображение
непрерывно, если

 ,
такое, что если
,
такое, что если
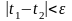 ,
то
,
то

 .
Если отображение
.
Если отображение
 непрерывно в каждой точке М, то оно
непрерывно и на всём множестве М.
непрерывно в каждой точке М, то оно
непрерывно и на всём множестве М.
Непрерывное отображение отрезка
в пространстве
называется линией в пространстве.
Также под линией будем понимать образ,
полученный при таком отображении. Линии
в пространстве удобно описывать в виде
 ,
причём если эти векторы откладывать от
одной точки.
,
причём если эти векторы откладывать от
одной точки.
Рассмотрим случай, когда образы двух
векторных функций совпадают, то есть
,
 ,
где
,
где
 ,
,
 .
Эти две линии определяют одну линию,
если существует монотонная функция
.
Эти две линии определяют одну линию,
если существует монотонная функция
 ,
,
 ,
,
 ,
такая что
,
такая что
 .
.
Линию
 назовем гладкой, если векторная
функция
(где
),
определяющая эту линию, имеет непрерывную
производную
во всех точках отрезка
.
назовем гладкой, если векторная
функция
(где
),
определяющая эту линию, имеет непрерывную
производную
во всех точках отрезка
.
Всякая гадкая линия, заданная уравнением
(где
),
имеет конечную дину, которая может
быть вычислена по следующей формуле:
 .
Когда в качестве параметра выбрана
длина линии
.
Когда в качестве параметра выбрана
длина линии
 ,то
говорят, что линия задана в натуральной
параметризации, а сам параметр l
называется натуральным параметром.
,то
говорят, что линия задана в натуральной
параметризации, а сам параметр l
называется натуральным параметром.
Линия L, заданная уравнением , называется кусочно-гладкой, если отрезок можно разделить на конечное множество отрезков, на каждом из которых линия будет гладкой.
Кривая L называется спрямляемой, если множество длин всевозможных ломанных, вписанных в кривую указанным выше образом, ограничено. Точная верхняя грань этого множества называется длиной дуги кривой.





Свойства длины дуги кривой:
1◦. Если кривая L1 является частью спрямляемой кривой L, то кривая L1 также спрямляема.
2◦Если кривая L разбита точкой N на две спрямляемые части L1 и L2, то кривая L спрямляема и для длин дуг кривых L1, L2 и L справедливо соотношение L1 + L2 = L
3◦ Обозначим через l(t) длину дуги кривой L соответствующей значениям параметра из отрезка[a, t]. Функция l(t) строго монотонна и непрерывна на отрезке [a, b] и положительна при t > a. Если выполнены условия теоремы 1.4, то функция l(t) имеет вид

Пусть r’ (t) != 0. Тогда существует функция t = t(l), обратная к функции l = l(t) и дифференци-
руема столько раз, сколько и функция r(t).Функция l(t) называется натуральным параметром кривой.
