3.5. Вихревое и безвихревое (потенциальное) движения

Напомним некоторые дифференциальные операции с векторами, известные из векторного анализа. Для этого воспользуемся векторным оператором Гамильтона

(3.37)

и проделаем некоторые формальные операции.

Из векторной алгебры известно, что скалярное произведение орт будет

;

, (3.38)

а их векторное произведение равно

;

, (3.39)

поэтому получим следующие операции с оператором .

1. Действие оператора на скалярную функцию , равное

, (3.40)

называется градиентом скалярной фукнции. есть вектор, который обладает, как будет показано далее, некоторыми особенностями, и называется он потенциальным вектором.

2. Скалярное произведение оператора на вектор

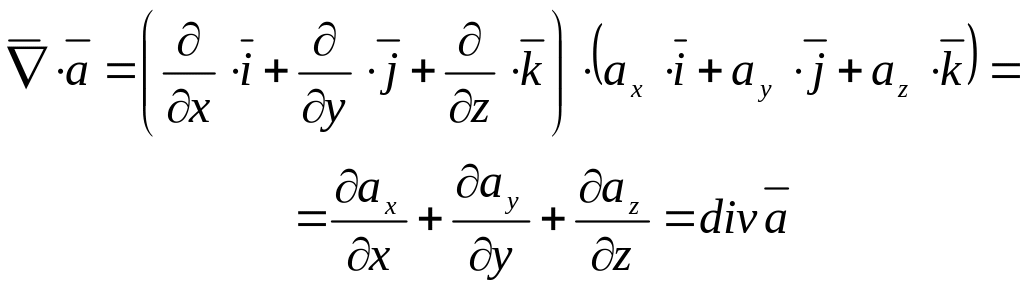(3.41)

есть величина скалярная и называется дивергенцией или расходимостью вектора.

3. Векторное произведение оператора на вектор

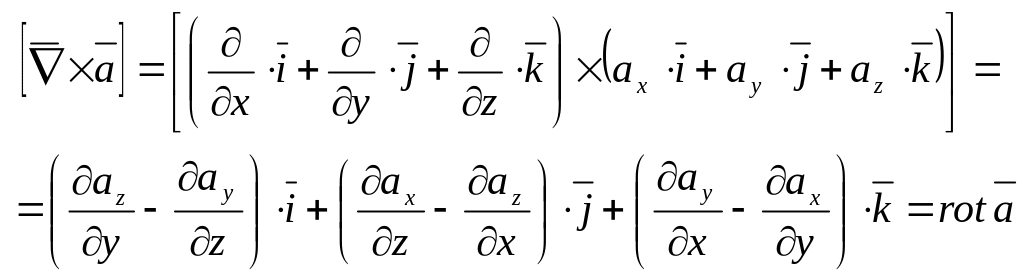(3.42)

есть величина векторная и называется она вихрем или ротором вектора.

Заметим, что скалярное произведение оператора на

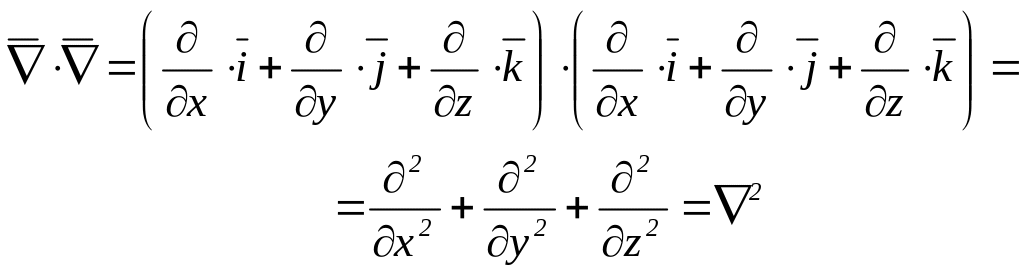(3.43)

есть оператор Лапласса. Применяя этот оператор к скалярной функции , получим

. (3.44)

Пользуясь оператором Гамильтона, легко получить следующие дифференциальные операции второго порядка:

; (3.45)

. (3.46)

Очевидно, что первое выражение обращается в нуль потому, что векторное произведение параллельных векторов ( и ) равно нулю, а второе - обращается в нуль потому, что здесь имеет место скалярное произведение взаимно перпендикулярных векторов: и .

Применим указанные операции в механике сплошных сред. Для определения физического смысла величины вектора рассмотрим поле любой скалярной величины, встречающееся в механике (температура, плотность, давление и пр.). В скалярном поле характерными линиями, определяющими поле, являются линии равных значений рассматриваемой величины. Для температуры это изотермы, для давлений - изобары, для проекций скоростей - изотахи и т.д. В качестве примера на рис. 3.5 приведены изотахи для расходных составляющих скоростей в выходном сечении патрубка турбины.

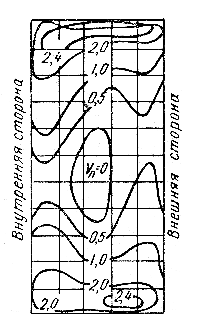
Рис. 3.5. Изотахи в выходном сечении патрубка турбины

В непрерывном поле скалярной величины через любую точку пространства можно провести линию постоянного значения. При этом в каждой точке скалярного поля значение производной от рассматриваемой величины будет зависеть от выбора направления. По направлениям касательных к линиям постоянного значения производные равны нулю, а по нормали к этой линии производная будет иметь наибольшее значение. Градиент скалярной функции есть вектор, направленный по нормали к линии постоянного значения скалярной функции в сторону увеличения этой функции и равный по величине производной от функции по направлению указанной нормали.

Таким образом, видно, что градиенты скалярного поля составляют векторное поле.

Рассмотрим физический смысл вихря вектора скорости. Из ранее приведенного определения следует, что

. (3.47)

Напомним уже известное понятие вращения твердого тела. Пусть некоторое тело вращается с угловой скоростью вокруг оси z. Тогда из рис. 3.6 видно, что величина скорости точки тела М будет равна , а ее проекции на оси х и у соответственно и .

Рис. 3.6. Схема скоростей вращающегося тела

Определив значения и , получим, что

, (3.48)

т.е. . (3.49)

Если аналогичным образом рассмотреть вращение твердого тела вокруг осей х и у, то соответственно найдем

; (3.50)

. (3.51)

Следовательно, вихрь вектора скорости жидкой частицы может быть определен вектором угловой скорости

. (3.52)

а модуль этого вектора равен

. (3.53)

Физически неравенство нулю значения в какой-либо точке потока означает, что в этой точке имеет место вращение элементарного объема. Никакого видимого вращения жидкости при этом в этой точке может и не быть. В качестве примера рассмотрим поток, в котором , a . Очевидно, для такого потока , a . Следовательно, это поток вихревой, так как , хотя никакого видимого вращения потока нет. Таким образом, вихрь отражает наличие вращательного движения только для элементарного объема.

Например, наблюдая за движением лодки в воде, легко видеть вихри, образующиеся за кормой лодки. Но, согласно введенному определению вихря, вихревое движение жидкости будет иметь место не только за кормой лодки, но и в непосредственной близости к корпусу лодки, где скорость изменяется довольно сильно и .

Иногда вихревое движение отождествляют с турбулентным. Это совершенно разные понятия. Вихревое движение может быть и ламинарным и турбулентным, а, в свою очередь, ламинарное и турбулентное (осредненное) движения могут быть как вихревыми, так и безвихревыми.

Если вектор скорости есть потенциальный вектор, то, его можно представить в виде

. (3.54)

Следовательно, проекции скорости и будут равны

. (3.55)

Последнее условие означает, что величина есть потенциал скорости .

Очевидно, что если вектор скорости имеет потенциал, то в соответствии с формулами (3.54) и (3.45) будем иметь

. (3.56)

Такое движение, при котором , называется безвихревым или потенциальным движением жидкисти.

В гидродинамике широко применяется понятие циркуляции скорости. Если и векторном поле скоростей проведем отрезок кривой АВ (рис. 3.7), то криволинейный интеграл

(3.57)

определяет величину циркуляции вектора скорости по контуру s на участке АВ.

Рис. 3.7. Схема циркуляции скорости

Если кривая, по которой определяется циркуляция, замкнутая, то величина циркуляции определяется интегралом по замкнутому контуру

. (3.58)

Легко видеть, что при наличии потенциала скоростей в векторном поле циркуляция скорости на участке АВ определяется разностью значений потенциала скоростей в точках А и В. Действительно, учитывая выражения (3.55), получим

.(3.59)

Когда контур АВ замкнутый и внутри не содержится никаких особенностей, то циркуляция по этому контуру будет равна нулю, так как .

Вихри скоростей образуют векторное поле, поэтому в нем можно получить векторные линии и векторные трубки.

Линия, в каждой точке которой вихри вектора скорости или вектора угловых скоростей вращения частиц касательны к ней, называется вихревой линией.

Уравнение вихревых линий, как следует из выражения (3.12), будет

. (3.60)

Если в пространстве, заполненном вихрями, взять некоторый замкнутый контур (не являющийся вихревой линией) и через каждую точку этого контура провести вихревые линии, то образуется вихревая поверхность. Часть жидкости, ограниченная этой поверхностью, называется вихревой трубкой. Когда замкнутый контур бесконечно мал, то вихревая трубка называется элементарной.

Из определения вихревой липни и вихревой поверхности следует, что в любой точке таких линий и поверхностей нормальная составляющая вихря скорости равна нулю.

Следовательно, если ввести понятие о потоке вектора вихря скорости, равном в соответствии с формулой (3.16)

,

то поток вектора вихря скорости через вихревую поверхность равен нулю.

Из векторного анализа известно, что поток любого вектора через любую замкнутую поверхность, внутри которой нет особенностей, равен нулю. Из этой теоремы векторного анализа вытекает, что и поток вихря сквозь любую замкнутую поверхность тоже равен нулю

. (3.61)

Выделим в вихревой трубке (рис. 3.8) некоторую замкнутую поверхность, образованную двумя любыми поперечными сечениями и и боковой поверхностью .

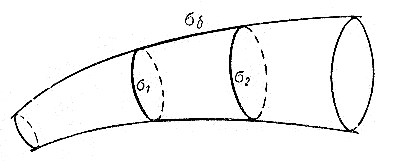
Рис. 3.8. Схема вихревой трубки

Так как поток вихря по боковой поверхности равен нулю, то, согласно формуле (3.61), следует

. (3.62)

Из полученного равенства вытекает следующее свойство вихревых трубок, известное в кинематике, как вторая теорема Гельмгольца: поток вектора вихря скорости сквозь произвольно проведенное поперечное сечение вихревой трубки в данный момент времени одинаков вдоль всей трубки.

Из этой теоремы следует, что поток вихря есть величина, характерная для всей вихревой трубки. Поэтому поток вихря принимают за характеристику вихревой трубки и называют интенсивностью вихревой трубки

. (3.63)

Иногда интенсивность вихревой трубки выражают через угловую скорость следующим образом:

. (3.64)

Если величина вихря постоянна по поперечному сечению вихревой трубки, то вторую теорему Гельмгольца можно записать в виде

. (3.65)

Из этой теоремы вытекают очень важные следствия:

1) сечение вихревой трубки нигде не может стать равным нулю, так как в этом сечении скорость вращения частиц должна стать бесконечной, что физически невозможно;

2) вихревые трубки не могут заканчиваться внутри жидкости: они либо замыкаются на себя, образуя вихревые кольца (рис. 3.9), либо «опираются» на стенку или на свободную поверхность.

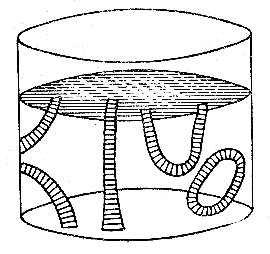
Рис. 3.9. Схемы вихревых колец

К последнему типу вихрей принадлежат наблюдаемые в природе водяные и воздушные смерчи. Прибор, иллюстрирующий образование вихря, показан на рис. 3.10.

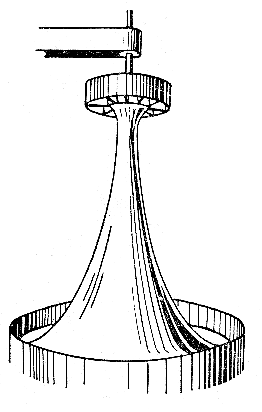
Рис. 3.10. Прибор для образования вихря

Вращение шкива, имеющего несколько радиальных перегородок, закручивает воздух. В области разрежения, создаваемого воздушным вихрем, вода поднимается и образует искусственный смерч.

В идеальной жидкости при наличии массовых сил, обладающих однозначным потенциалом, интенсивность вихря не меняется со временем. Таким образом, вихри идеальной жидкости не могут менять в пространстве и во времени своей интенсивности. Они должны существовать вечно, они не могут возникать и вырождаться. В действительности, в реальной жидкости из-за наличия вязкости вихри зарождаются и затем диффундируют, т.е. вырождаются.

Из теоретической механики известно, что скорость любой точки М твердого тела определяется геометрической суммой скорости поступательного движения вместе с некоторым полюсом О и скорости вращения вокруг мгновенной оси, проходящей через полюс О, т.е.

, (3.66)

где - угловая скорость вращения;

- радиус-вектор точки М.

Аналогичная теорема, являясь основной теоремой кинематики, имеет место и для скоростей движения элементарных жидких объемов. Эта теорема гласит: скорость движения любой точки жидкой частицы складывается из скорости квазитвердого движения и скорости деформации , т. е.

. (3.67)

Скорость квазитвердого движения, как следует из формулы (3.66), в свою очередь складывается из поступательной скорости и скорости вращения.

Для доказательства этой теоремы определим в данный момент времени поле скоростей в окрестности точки (рис. 3.11).

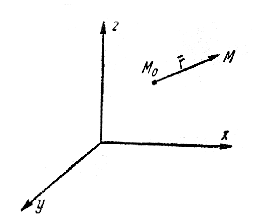
Рис. 3.11. Поле скоростей в окрестностях точки

Пусть в точке с координатами и скорости будут иметь значения и .

В соответствии с рядом Тейлора можно найти значение скоростей и в точке , расположенной в окрестности точки . С точностью до малых первого порядка они будут равны

;

; (3.68)

,

где .

Прибавив и вычтя в первом уравнении (3.68) величину

, (3.69)

получим

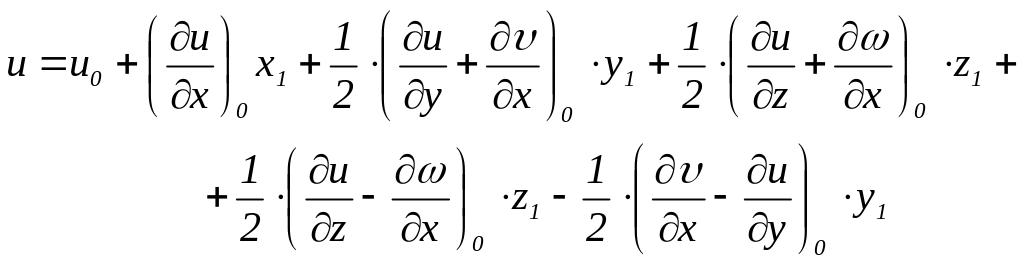(3.70)

Для дальнейших преобразований введем следующие обозначения:

;

;

;

;

;

;

. (3.71)

Тогда уравнение (3.70) будет

, (3.72)

а остальные два уравнения (3.68) после аналогичных преобразований примут вид

; (3.73)

. (3.74)

Первые два слагаемых правой части полученных уравнений можно рассматривать как скорости квазитвердого движения, третьи слагаемые являются скоростями деформации элементарного объема.

Так как, согласно рис 3.11,

, (3.75)

то

;

; (3.76)

.

Для характеристики скорости деформации введем функцию F, равную

, (3.77)

Тогда

;

; (3.78)

.

Используя выражения (3.76) и (3.78), окончательно получим

;

; (3.79)

,

или в векторном виде

, (3.80)

где - скорость поступательного движения;

- скорость вращательного движения вокруг мгновенной оси с угловой скоростью ;

grad F - скорость чистой деформации.

Скорость деформации жидкой частицы в точке М определяется следующей таблицей:

. (3.81)

Таблица S называется тензором скоростей деформации, a - компонентами или составляющими тензора скоростей деформации.

При этом , расположенные на диагонали таблицы, характеризуют скорости относительного удлинения (сжатия) жидких отрезков, a - скорости перекосов элементарного объема. Рассмотрим детально отдельные составляющие тензора скоростей деформаций.

Возьмем сферическую частицу движущейся жидкости (рис. 3.12) и посмотрим, что с ней произойдет через время dt.

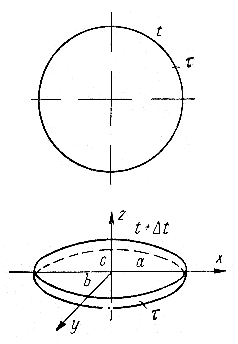
Рис. 3.12. Схема деформации сферической частицы

жидкости

Сферическая частица в момент времени t имела объем , через время dt эта частица может остаться сферической или измениться, но измениться незначительно, ибо время dt очень мало. Пусть - объем эллипсоида с полуосями и с, образовавшегося из сферы за время dt. Найдем изменение объема. Обычно берут относительное изменение объема в единицу времени, т.е. .

Объем шара равен

, (3.82)

объем эллипсоида запишется

, (3.83)

причем его полуоси будут

;

; (3.84)

,

где - изменение скорости по осям координат.

Тогда

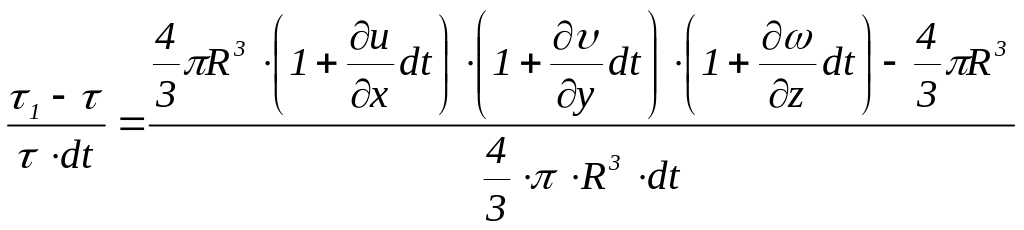. (3.85)

После раскрытия скобок и пренебрежения величинами второго и третьего порядка малости будем иметь

. (3.86)

характеризует собой расходимость вектора скорости. Используя старые обозначения

. (3.87)

получим

. (3.88)

Отсюда видно, что совокупность диагональных составляющих тензора скоростей деформации (3.81) выражает расходимость вектора скорости, характеризующего собой скорость (быстроту) относительного изменения объема жидкой частицы.

Для характеристики компонентов тензора скоростей деформации рассмотрим детально один из них, например . Эта величина характеризует скорость деформации сдвига жидкой частицы в плоскости ху.

Пусть в некоторый момент времени жидкая частица будет иметь в плоскости ху форму квадрата со сторонами dx и dy (рис. 3.13).

Рис. 3.13. Схема деформации жидкой частицы

Так как скорости в вершинах квадрата будут неодинаковы (рис. 3.13, а), то через единицу времени рассматриваемый квадрат примет форму параллелограмма (рис. 3.13, б). При этом угол сдвига между осью игреков и стороной О'С' будет равен

, (3.89)

а угол между осью иксов и стороной О'А' соответственно

. (3.90)

Так как мы рассмотрели изменение прямого угла СОА за единицу времени, то величина

(3.91)

будет характеризовать скорость изменения первоначального угла АОС. Следовательно,

, (3.92)

т.е. характеризует скорость деформации скашивания угла или сдвига в плоскости ху.

Аналогичным образом можно показать, что и характеризуют скорости деформации сдвига в плоскостях уz и хz.

Таким образом, скорость деформации элементарной жидкой частицы полностью определяется тензором (3.81).

Второй важной кинематической теоремой о вихрях является теорема Стокса: интенсивность вихревой трубки равна циркуляции скорости по замкнутому контуру, один раз опоясывающему вихревую трубку. Докажем эту теорему для более общего случая с такой формулировкой: поток вектора вихря скорости через любую поверхность, опирающуюся на некоторый замкнутый контур, равен циркуляции скорости по этому контуру.

Вначале определим величину циркуляции скорости по некоторому бесконечно малому контуру, который находится в движущейся жидкости, имеющей непрерывно распределенные вихри. Пусть контур ОСВАО (рис. 3.13, а) лежит в плоскости ху и имеет стороны dx и dy. Если в точке О проекции скоростей будут и , то в точках С и А величины скоростей, совпадающих по направлению со сторонами СВ и АВ, равны соответственно

; (3.93)

. (3.94)

Тогда циркуляция по контуру ОСВАО будет равна

(3.95)

или, раскрывая скобки и производя сокращение, получим

. (3.96)

Так как является проекцией вихря на ось z, нормальную к площадке dxdy, то правая часть последнего равенства является потоком вектора вихря скорости через площадку dxdy. Проделав аналогичные вычисления для площадок dxdz и dydz и распространив эти результаты на элементарную площадку , произвольно расположенную в пространстве, получим

. (3.97)

Последнее соотношение означает, что циркуляция по бесконечно малому прямоугольному контуру равна потоку вихря через площадку, ограниченную этим контуром, или интенсивности элементарной вихревой трубки.

Если теперь возьмем произвольный плоский контур с любой конечной площадью, то, разбив, как это показано на рис. 3.14, всю площадь на элементарные прямоугольники и вычислив циркуляцию по контурам этих прямоугольников, в результате суммирования по всей площади получим циркуляцию вдоль всего контура, равную

. (3.98)

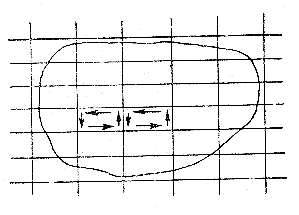
Рис. 3.14. Циркуляция скорости через плоский контур

и произвольную поверхность

Полученную формулу можно применить не только для плоской площадки, а и для некоторой произвольной поверхности (рис. 3.14). Разбив эту поверхность на бесконечно большое количество бесконечно малых площадок , получим величину циркуляции для каждой площадки (считая ее плоской), равную

. (3.99)

Суммируя циркуляции по элементарным площадкам, получим циркуляцию по поверхности

. (3.100)

Таким образом, теорему Стокса можно считать доказанной для произвольного контура, а следовательно, и для контура, опоясывающего вихревую трубку.

Формула (3.100) после подстановки выражения для циркуляции (3.57) будет иметь вид

. (3.101)

Заменив вектор скорости на некоторый вектор а, получим известную из векторного анализа формулу Стокса, связывающую интеграл по контуру с интегралом по поверхности, опирающейся на этот контур

, (3.102)

где .