
- •Геометрические векторы. Линейные операции над ними. Коллинеарность.
- •Базис. Разложение по базису. Координаты вектора.
- •Линейные операции над векторами в координатной форме.
- •Проекция вектора на ось и ее свойства
- •Декартова прямоугольная система координат
- •Определители. Минор, алгебраическое дополнение.
- •Вычисление определителей 2-го и 3-го порядков. Минор. Алгебраическое дополнение.
- •Вычисление определителей n-ого порядка. Треугольные диагональные матрицы.
- •Решение матричных уравнений. Примеры. Их связь с формулами Крамара.
- •Системы линейных уравнений. Матричная и векторная запись. Основные понятия.
- •Правило Крамара для решения систем линейных уравнений.
- •Ранг матрицы. Элементарные преобразования матрицы.
- •Обратная матрица (определение вычисление единственности). Вырожденные матрицы. Св-ва обратных матриц.
- •Теорема о ранге матрицы и её следствия. Задача о нахождении линейно независимой подсистемы в системе векторов.
- •Теорема о базисном миноре (с док.)
- •Теорема о ранге матрицы и её следствия. Задача о нахождении линейно независимой подсистемы в системе векторов.
- •Теорема Кронекера – Капели (с док.)
- •Базисные и свободные переменные. Геометрическая интерпретация решения системы линейных уравнений.
- •Решение систем линейных уравнений (слу). Свойства решений слу.
Обратная матрица (определение вычисление единственности). Вырожденные матрицы. Св-ва обратных матриц.
Опр. Матрица В
называется обратной матрицы А, если
выполняется следующее равенство:
![]() .
Обратную матрицу имеют только невырожденные
матрицы (detA
).
.
Обратную матрицу имеют только невырожденные
матрицы (detA
).
![]() или
или
![]()
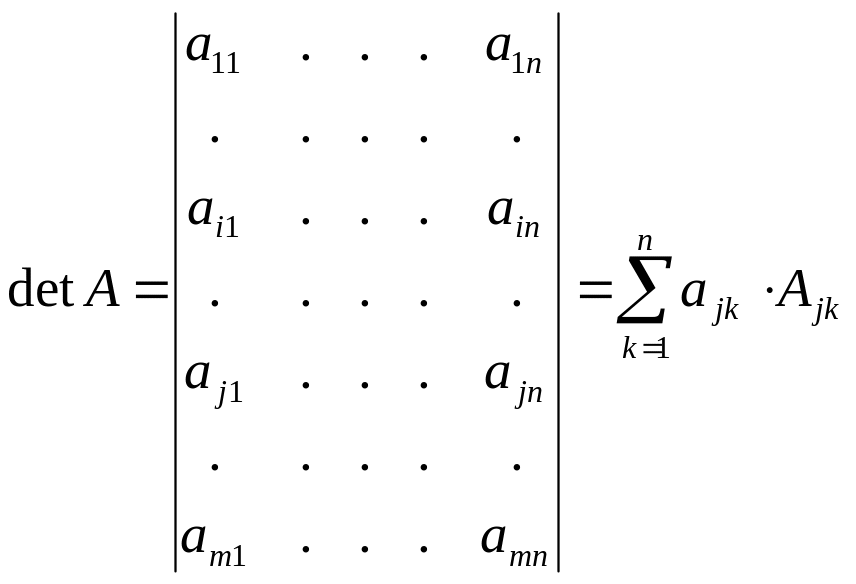
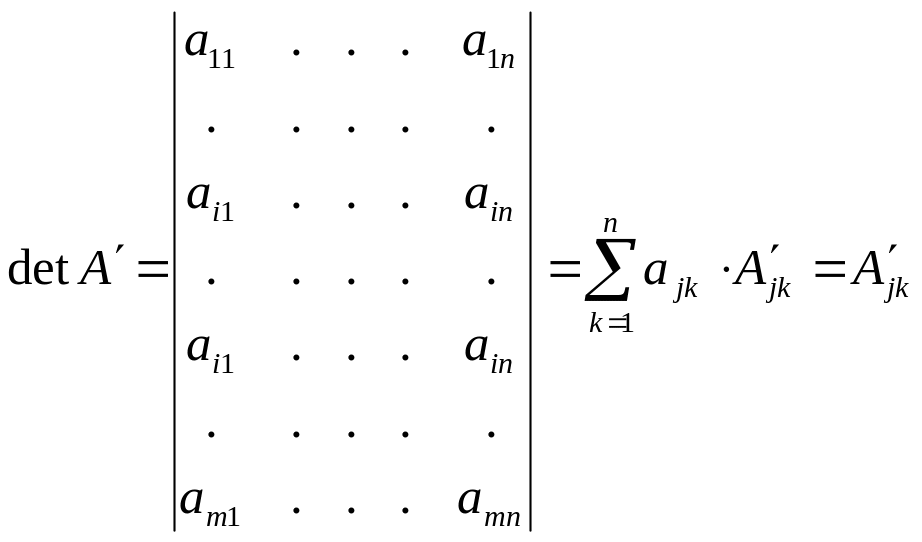
На j-том
месте в последней матрице стоит i-тая
строка detA’=0.
Разлагаем detA’=0
по j-той
строке:
![]() ,
т.е. сумма произведений элементов любой
строки на соответствующие алгебраические
дополнения другой строки равна нулю.
Теорема (о нахождении обратной матрицы
A-1)
Для любой невырожденной матрицы
существует единственная обратная
матрица А-1,
которая вычисляется по формуле:
,
т.е. сумма произведений элементов любой
строки на соответствующие алгебраические
дополнения другой строки равна нулю.
Теорема (о нахождении обратной матрицы
A-1)
Для любой невырожденной матрицы
существует единственная обратная
матрица А-1,
которая вычисляется по формуле:
![]() ,
где
,
где
![]() -
состоит из соответствующих алгебраических
дополнений – присоединённая матрица.
Доказательство:
-
состоит из соответствующих алгебраических
дополнений – присоединённая матрица.
Доказательство:
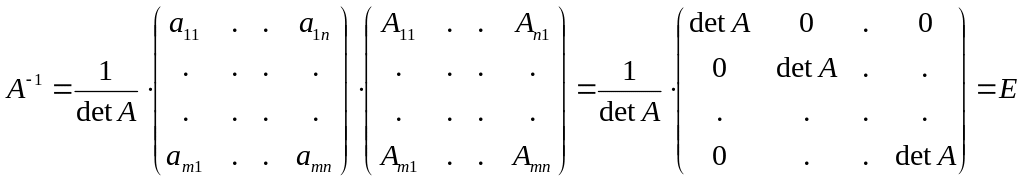 Докажем единственность: пусть
Докажем единственность: пусть
![]() и
и
![]() ,
,
тогда
![]()
Теорема о ранге матрицы и её следствия. Задача о нахождении линейно независимой подсистемы в системе векторов.
Теорема.
Если
ранг матрицы системы линейных форм
равен r,
то
существует r
линейно независимых форм, от которых
линейно зависят
все остальные формы.
Доказательство.
Пусть мы имеем систему m
линейных
форм
:
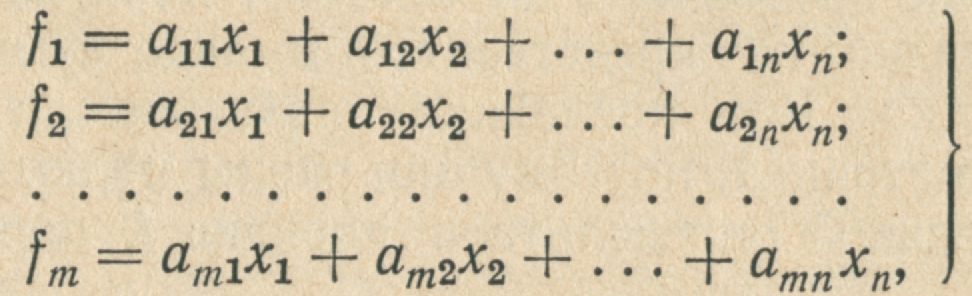
и пусть матрица из коэффициентов этой системы имеет ранг r. Следовательно, среди определителей, порождаемых матрицей М, есть хотя бы один определитель r-го порядка, отличный от нуля. Мы можем предположить, что один из таких определителей находится в левом верхнем углу матрицы М. Обозначим его через D. Это предположение не уменьшает общности наших рассуждений, так как если бы этого не было, то мы соответственным образом изменили бы нумерацию форм и неизвестных. Из нашего предположения следует, что первые r форм f1, f2, ... , fr линейно независимы. В самом деле, если бы они были зависимы, то одна из строк определителя D была бы линейной комбинацией других строк и он бы равнялся нулю, что противоречит условию. Покажем теперь, что всякая форма fk (k>r) линейно зависит от f1,f2,…,fr. Для этого достаточно показать, что k-я строка матрицы М есть линейная комбинация её первых r строк. Возьмём определитель (r+1)-го порядка:
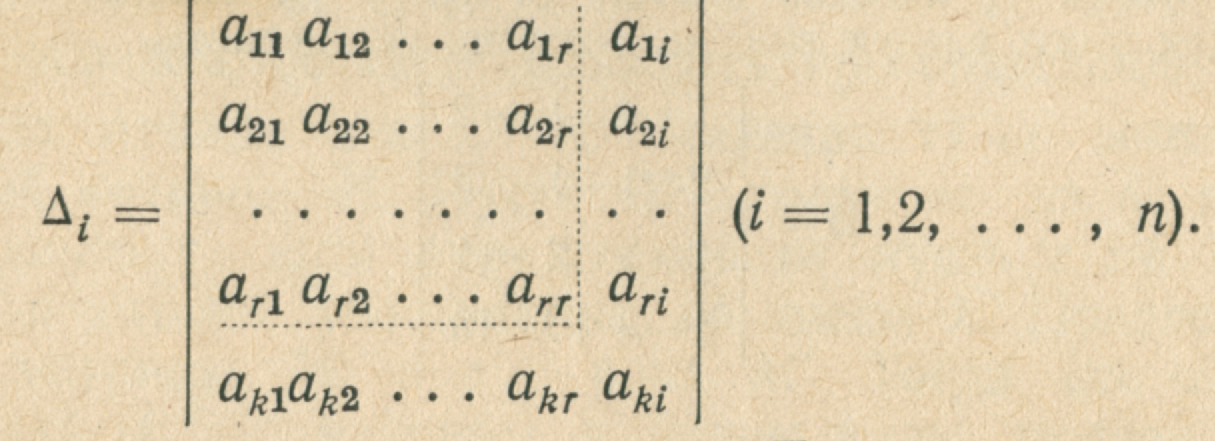 Этот
определитель равен нулю. Действительно,
если i
Этот
определитель равен нулю. Действительно,
если i![]() r,
то
r,
то
![]() будет иметь два одинаковых столбца,
поэтому
.
Если
же i
>
r,
то
будет определитель (r
+ 1)-го
порядка, порожденный
матрицей М
ранга
r,
поэтому и здесь
= 0. Разложим
определитель Д, по элементам последнего
столбца, обозначив
их алгебраические дополнения через
А1i,
А2i,.
. . , Аr+1i
{Аr+1i
— алгебраическое
дополнение элемента aki):
будет иметь два одинаковых столбца,
поэтому
.
Если
же i
>
r,
то
будет определитель (r
+ 1)-го
порядка, порожденный
матрицей М
ранга
r,
поэтому и здесь
= 0. Разложим
определитель Д, по элементам последнего
столбца, обозначив
их алгебраические дополнения через
А1i,
А2i,.
. . , Аr+1i
{Аr+1i
— алгебраическое
дополнение элемента aki):
![]()
Так как Ar+1i = D 0, то полученную зависимость можно разрешить относительно аki:
![]() (1) или обозначая
(1) или обозначая
![]() получаем
получаем
![]() .
.
Полученное соотношение (1) не только доказывает что k-z строка матрицы M есть линейная комбинация её первых r строк, но и даёт правило нахождения линейной зависимости.
Теорема о базисном миноре (с док.)
Строки базисного минора линейно независимы. Любая строка не входящая в базисный минор является линейной комбинацией базисных строк или строк базисного минора.
Теорема о ранге матрицы и её следствия. Задача о нахождении линейно независимой подсистемы в системе векторов.
Ранг матрицы равен максимальному числу линейно независимых подсистем. Если ранг матрицы равен r, то в качестве r - независимых строк можно взять: во-первых, те строки, которые остались ненулевыми, во-вторых, любые r – строк, для которых существует минор Mr 0 – такие миноры называются базисными.
