
- •Понятие множества. Примеры множеств. Способы задания множеств.
- •Пустое множество. Равные множества. Подмножества. Примеры.
- •Универсальное множество. Дополнение множества до универсального множества.
- •Кортеж. Декартово умножение множеств.
- •Отношения эквивалентности и порядка.
- •Отображения. Функции. Равномощные множества. Композиция отображений.
- •12.Мощность множества. Счетные множества. Мощность континуума.
- •14.Понятие перестановки. Число перестановок n-элементного множества.
- •16. Понятия размещения. Числа всех размещений из n элементов по k элементов.
- •17. Треугольник паскаля и его свойства. Бином ньютона, его свойства и некоторые приложения.
- •18. Метод рекуррентных соотношений (определение и примеры).
- •Решение рекуррентных соотношений. Примеры.
- •21. Линейные рекуррентные соотношения с постоянными коэффициентами.
- •Числа Фибоначчи, их свойства и приложения.
- •23.. Числа Каталана. Числа Стирлинга (1-го и 2-го рода), гармонические числа.
- •25. Производящие функции.
- •Целочисленные функции округления.
- •27.Иерархия.Асимптотическая аппроксимация.
- •29.Графы, ориентированные графы, псевдографы, мультиграфы.
- •31.Маршруты, пути.
- •32.Матричное задание графов.
- •33.Операции над графами, подграфы.
- •35. Поиск маршрутов в графах.
- •36.Деревья, свойства деревьев. Лес.
- •38.Эйлеровы графы и циклы.
- •40.Планарные графы.
- •41.Правильная раскраска вершин графов.
- •43.Принцип Дирихле.
- •45.Приложение теоремы Рамсея. Теорема Ван дер Вардена.
- •46.Двудольные графы. Теорема Кенига
Числа Фибоначчи, их свойства и приложения.
Числа Фибоначчи — это элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597,… в которой каждое последующее число равно сумме двух предыдущих чисел. Числа Фибоначчи1 F(n) определяются следующим образом: F(0) = 1, F(l) = 1, F(n + 2) = F(n + 1) + F(n). Числа Фибоначчи обладают множеством интересных математических свойств.
Вот лишь некоторые из них:
Соотношение Кассини:
![]()
Правило "сложения":
![]()
Из предыдущего равенства при
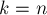 вытекает:
вытекает:
![]()
Из предыдущего равенста по индукции можно получить, что
![]() всегда
кратно
всегда
кратно ![]() .
.
Верно и обратное к предыдущему утверждение:
если ![]() кратно
,
то
кратно
,
то ![]() кратно
кратно ![]() .
.
НОД-равенство:
![]()
23.. Числа Каталана. Числа Стирлинга (1-го и 2-го рода), гармонические числа.
Числа
Каталана — числовая последовательность,
встречающаяся в удивительном числе
комбинаторных задач. Эта последовательность
названа в честь бельгийского математика
Каталана (Catalan), жившего в 19 веке, хотя
на самом деле она была известна ещё
Эйлеру (Euler), жившему за век до Каталана.
Первые несколько чисел Каталана ![]() (начиная
с нулевого): 1,1,2,5,14. Числа Каталана
встречаются в большом количестве задач
комбинаторики. Имеется две формулы для
чисел Каталана: рекуррентная и
аналитическая.
(начиная
с нулевого): 1,1,2,5,14. Числа Каталана
встречаются в большом количестве задач
комбинаторики. Имеется две формулы для
чисел Каталана: рекуррентная и
аналитическая.
![]() Рекуррентную формулу легко вывести из
задачи о правильных скобочных
последовательностях. Самой левой
открывающей скобке l соответствует
определённая закрывающая скобка r,
которая разбивает формулу две части,
каждая из которых в свою очередь является
правильной скобочной последовательностью.
Поэтому, если мы обозначим
Рекуррентную формулу легко вывести из
задачи о правильных скобочных
последовательностях. Самой левой
открывающей скобке l соответствует
определённая закрывающая скобка r,
которая разбивает формулу две части,
каждая из которых в свою очередь является
правильной скобочной последовательностью.
Поэтому, если мы обозначим ![]() ,
то для любого фиксированного
,
то для любого фиксированного ![]() будет
ровно
будет
ровно ![]() способов.
Суммируя это по всем допустимым
способов.
Суммируя это по всем допустимым ![]() ,
мы и получаем рекуррентную зависимость
на
.
,
мы и получаем рекуррентную зависимость
на
.![]() (здесь через
(здесь через ![]() обозначен,
как обычно, биномиальный коэффициент).
Эту формулу проще всего вывести из
задачи о монотонных путях.
обозначен,
как обычно, биномиальный коэффициент).
Эту формулу проще всего вывести из
задачи о монотонных путях.
Числа
Стирлинга первого рода s(n, k) —
это коэффициенты при последовательных
степенях переменной x в
многочлене [x]k:
[x]n =
∑k=0:n s(n, k)xk.Для
них определяются аналогичные рекуррентные
соотношения, что и для чисел второго
рода: s(n, n) = 1,
для n ≥ 0,s(n, 0) = 0,
для n > 0,
s(n, k) = s(n−1, k−1) +
(n−1)s(n−1, k),
для 0 < k < n.Число
Стирлинга второго рода S(n, k) —
это число разбиений n-элементного
множества на k блоков,
т. е. S(n, k) = |Πk(X)|,где
множество X состоит
из n элементов.
Например, S(4, 2) = 7.Любопытны
некоторые тождества, связанные с числами
Стирлинга второго рода: S(n, n) = 1,
для n ≥ 0,
S(n, 0) = 0,
для n > 0,
S(n, k) = S(n−1, k−1) + kS(n−1, k),
для 0 < k < n
xn =
∑k=0:n S(n, k)[x]k,
для n ≥ 0,
где [x]k = x(x−1)…(x−k+1).В математике, n-м гармоническим
числом называется
сумма обратных
величин первых n последовательных
чисел натурального ряда:
![]() .
Гармонические числа являются частичными
суммами гармонического ряда.
.
Гармонические числа являются частичными
суммами гармонического ряда.
24.. Суммы и рекуррентные соотношения. Преобразования сумм.
