49 Применение дифференциала к приближенным вычислениям

Пусть нам известно значение функции y0=f(x0) и ее производной y0' = f '(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x.

Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x0)·Δx.

Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f'(x0)·Δx.

Откуда

f(x) ≈ f(x0) + f'(x0)·Δx

Примеры.

y = x2 – 2x. Найти приближенно, с помощью дифференциала, изменение y (т.е. Δy), когда x изменяется от 3 до 3,01.

Имеем Δy≈dy=f'(x)·Δx.

f'(x)=2x – 2 ,f'(3)=4, Δx=0,01.

Поэтому Δy ≈ 4·0,01 = 0,04.

Дифференциал суммы, произведения, частного

Теорема 13. Пусть функции u = u(x), v = v(x) дифференцируемы.

Тогда

Доказательство

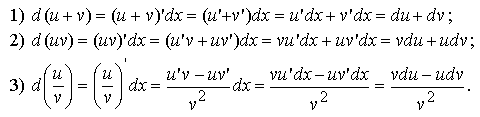
Теорема доказана.

50. Функция, заданная параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.

Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем

Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х.

Пусть  

Найти у'х.

Решение: Имеем   x't=3t2,   y't=2t.   Следовательно,   у'х=2t/t2,   т. е. 

В этом можно убедиться, найдя непосредственно зависимость у от х.

Действительно,    Тогда    Отсюда  т. е.

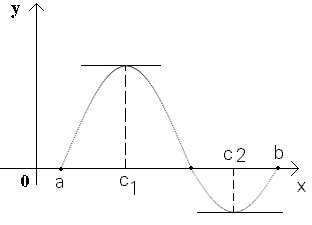
51. Теорема Ролля. Если функция y= f(x) непрерывна на отрезке [a; b], дифференцируема во всех внутренних точках этого отрезка (т.е. на (а; b)) и на концах отрезка обращается в нуль f(a) = f(b) = 0, то на (a; b) найдется хотя бы одна точка c  (a; b), в которой f'(c) = 0.

Доказательство. Так как функция f(x) непрерывна на [a; b], то по одной из теорем о непрерывных функциях она достигает на этом отрезке наибольшего значения и наименьшего. Пусть 

Заметим, что если М = m, то f(x) = const = 0 (по условию теоремы f(a)=f(b)=0) и, следовательно,f'(x)=0при всех x  [a; b] .

Предположим, что M≠m, тогда, по крайней мере, одно из этих чисел отлично от нуля. Для определенности будем считать, что М ≠0 и М > 0.

Пусть в точке x = c f(c)=М, при этом c≠a и с ≠ b, т.к. f(a)=f(b)=0. Придадим значению c приращение Δxи рассмотрим новую точку c+Δx. Поскольку f(c) – наибольшее значение функции, то f(c+Δx) – f(c)≤0 для любого Δx. Отсюда следует, что

Переходя в этих неравенствах к пределу при Δx→0 и учитывая, что производная при x = c существует, будем иметь:

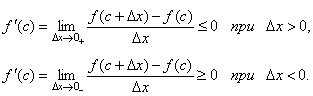
Но неравенства f'(c) ≤ 0 и f'(c) ≥ 0 одновременно возможны лишь в случае, когда

f'(c)=0. Теорема доказана.

52.

Теорема Лагранжа. Если функция y= f(x) непрерывна на [a; b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a; b] найдется хотя бы одна точка c, a<c<b такая, чтоf(b) – f(a)=f'(c)(b – a).

Доказательство. Обозначим   и рассмотрим вспомогательную функцию F(x) = f(x) – f(a) – k(x – a).

Выясним геометрический смысл введенной функции. Для этого рассмотрим график данной функции на [a; b] и напишем уравнение хорды АВ. Заметим, что угловой коэффициент хорды  и она проходит через точку A(а; f(a)). Следовательно, ее уравнение

y = f(a) + k(x – a).

Но F(x)=f(x)–[f(a)+k(x–a)]. ПоэтомуF(x) при каждом xесть разность ординат графика y= f(x) и хорды, соответствующих точкам с одинаковой абсциссой.

Легко видеть, что F(x) непрерывна на [a; b] , как разность непрерывных функций. Эта функция дифференцируема внутри [a; b] и F(a)=F(b)=0. Следовательно, к функции F(x) можно применить теорему Ролля. Согласно этой теореме найдется точкаc  (a; b), что F'(c)=0. Но F '(x) = f'(x) – k, а значит,F'(c) = f'(c) – k = 0.

Подставляя в это равенство значение k, получим

,

что и требовалось доказать.

Теорема Коши. Если f(x) и g(x) – две функции, непрерывные на [a; b] и дифференцируемые внутри него, причем g'(x) ≠ 0 при всех x  (a; b), то внутри отрезка [a; b] найдется хотя бы одна точка c  (a;b), что  .

Доказательство.Определим число  . Заметим, что g(b) – g(a) ≠ 0, т.к. в противном случае выполнялось бы равенство g(b)=g(a) и по теореме Ролля в некоторой точке d  (a; b)g'(d) = 0. Это противоречит условию теоремы.

Составим вспомогательную функцию.

F(x) = f(x) – f(a) – k[g(x) – g(a)].

Несложно заметить, что F(a)=F(b)=0. Функция F(x) удовлетворяет на [a;b] всем условиям теоремы Ролля. Следовательно, найдется число сÎ(a; b) такое, что F'(c) = 0. Но

F'(x) = f'(x) – k·g(x), а значит F'(c) = f'(c) – k·g'(c) = 0,

откуда .

Заметим, что теорему Коши нельзя     доказать, применяя теорему Лагранжа к числителю и знаменателю дроби k. Объясните почему.