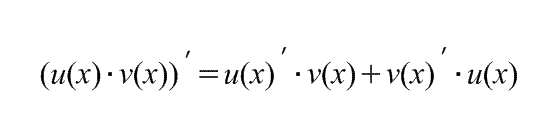42. Производная степенной функции.
Формула для вычисления производной степенной функции xn, где n — произвольное натуральное число, большее 1, такова:
(xn)’=nxn-1 (1)
Формула производной функции х2 уже известна: (х2)' = 2х.
Производная показательной и логарифмической функции |
|
Предполагается, что основание a показательной и логарифмической функции больше нуля и не равно единице: a > 0, a ≠ 1. Производная показательной функции y = ax с основанием a определяется формулой
где ln a - натуральный логарифм a, т.е. логарифм a по основанию е, приблизительно равному 2,718281828... (2.7, затем два раза год рождения Л.Н.Толстого). Знаменитое трансцендентное число е можно вычислить с любой степенью точности с помощью различных компьютерных алгоритмов. Если a = е, то получаем красивый результат в виде
Производная логарифмической функции y = loga x определяется выражением
Для натурального логарифма y = ln x производная равна
|
43 Производная алгебраической суммы функций
выражается следующей теоремой.
Теорема 1. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
(u±v)' = u'±v'
Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,
(u — v + w)' = u' — v' + w'
Производную произведения функций определяет
Теорема 2. Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой, т. е.
(uv)' = u'v + uv'
Следствие 1. Постоянный множитель можно выносить за знак производной (cv)' = cv' (с = const).
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные.
Например, (uvw)' = u'vw + uv'w + uvw'
Производная суммы (функций): |
|
Производная произведения (функций): |
|
44. Производная частного функций.
Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле
Производные тригонометрических функций. Формула производной косинуса, тангенса и котангенса.
Докажем, что функции y = cos x, y = tg x, y = ctg x имеет производные в каждой точке своей области опредления и справедливы формулы:
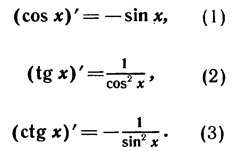
Вывод формулы (1) основан на равенствах
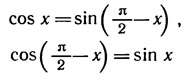
и правиле дифференцирования сложной функции:
Чтобы доказать справедливаость формул (2)и (3), применим формулу для нахождения производной частного и выведенные формулы производной синуса и косинуса (1):
45. Теорема (о дифференцировании обратной функции)
Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е
Производные от обратных тригонометрических функций
