18 ,19 Итерационные методы решения систем:
1)Метод простой итерации:
Представим матрицу A в виде A=S – T и матрица S – единичная матрица соответствующего размера, умноженная на главную диагональ матрицы A. Тогда система Ax=b эквивалентна системе Sx=Tx+b.
Итерационный процесс: Sx(K+1)= Tx(k) + b.
Так последовательность x(k) сходится к точному решению x.
2)Метод Зейделя:
ТО же самое но в качестве матрицы S используем нижнюю треугольную матрицу, элементы которой на главной диагонали и ниже равны соответствующим элементам матрицы A.
Теорема. Пусть A – матрица с диагональным преобладанием, тогда методы простой итерации и Зейделя сходятся.
3)Метод последовательной верхней релаксации.
Пусть
,
A=D+L+U,
где D,L,U
– соответственно диагональная, нижняя
и верхняя треугольная части матрицы A
с нулями на главной диагонали. Тогда
итерационный процесс имеет вид:
(D + ωL) x(K+1)=((1-ω) D – ωU) x(K) + ωb.
19.
Векторное произведение двух векторов
и его приложения.
Необходимое
и
достаточное условие коллинеарности
двух векторов.Три
некомпланарных вектора
,
и
,
взятые в указанном порядке, образуют
правую
тройку,
если с конца третьего вектора
кратчайший поворот от первого вектора
ко второму вектору
виден совершающимся против часовой
стрелки, и левую
– если по часовой.
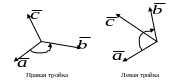
Векторным произведением вектора на вектор называется вектор , который:
а)
перпендикулярен векторам
и
,
т.е.
и
;
б)
имеет длину, численно равную площади
параллелограмма, построенного на
векторах
и
как на сторонах, т.е.
, где
(угол между)
в) векторы , и образуют правую тройку.
Векторное
произведение обозначается
или
.
Из
определения векторного произведения
непосредственно вытекают следующие
соотношения между ортами
,
и
:
,
,
.
Теорема
(о свойствах векторного произведения).
Пусть
,
и
- произвольные векторы, а
- любой скаляр. Тогда справедливы
следующие соотношения:
а)
;
б)
;
в)
два ненулевых вектора
и
коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулевому вектору,
т.е.
;
г)
;
Доказательство.
а)
векторы
и
коллинеарны, имеют одинаковые модули
(площадь параллелограмма остается
неизменной), но противоположно направлены
(тройки
и
противоположной ориентации). Стало быть
.
б)
пусть
.
Вектор
перпендикулярен векторам
и
.
вектор также перпендикулярен векторам
и
(векторы
и
лежат в одной плоскости). Значит, векторы
и
коллинеарны. Очевидно, что и направления
их совпадают. Имеют одинаковую длину:
и
.
Поэтому .
в)
если
||
,
то угол между ними равен 0 или
.
Но тогда
. Значит,
. Если же
,
то
. Но тогда
или
,
т.е.
||
.
В частности,
.
Получим выражение для векторного произведения через координаты. Применим таблицу векторов , и :
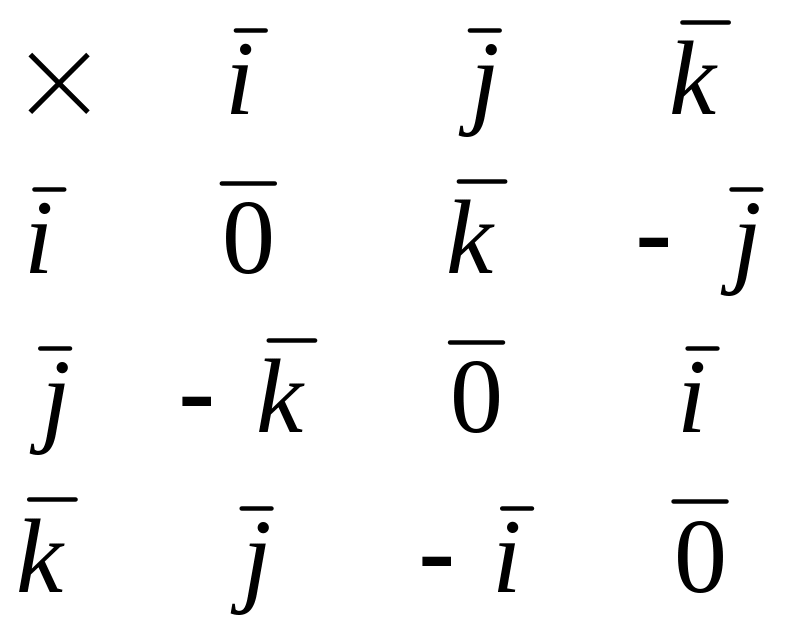Пусть
заданы два вектора
и
.
Найдем векторное произведение этих
векторов, перемножив их как многочлены
(с использованием свойств векторного
произведения):
,т.е.
=
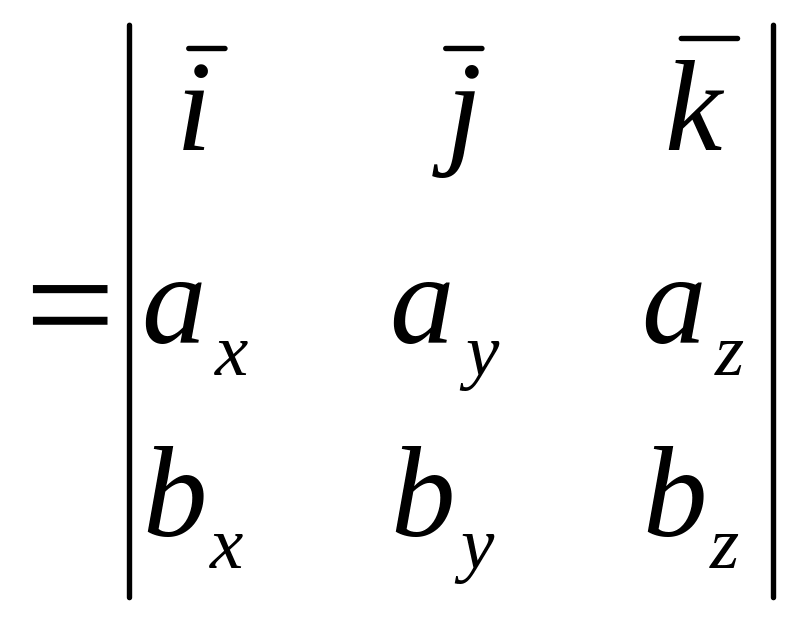
Если || , то ( и наоборот):
=
Нахождение площади
параллелограмма и треугольника.
Согласно определению векторного
произведения векторов
и
т.е.
.
Значит,
