12.Линейные операторы. Примеры. Матрица линейного оператора в фиксированном базисе. Действия над линейными операторами.

Пусть L-лин.прост-во над полем действ.чисел. Скажем,что в L задан оператор(преобразование)φ,если каждому вектору х L поставлен в соот-вие опред. Ектор φ(х) L.

Оп-р φ назыв.лин-ным,если для любых двух векторов х,у L и произвольного числа λ R выполн.след.условия:1) φ(х+у)= φ(х)+ φ(у);2) φ(λх)=λφ(х). Вектор φ(х) назыв.образом вектора х,а вектор х-прообразом вектора φ(х) при преобразовании φ.

Аφ=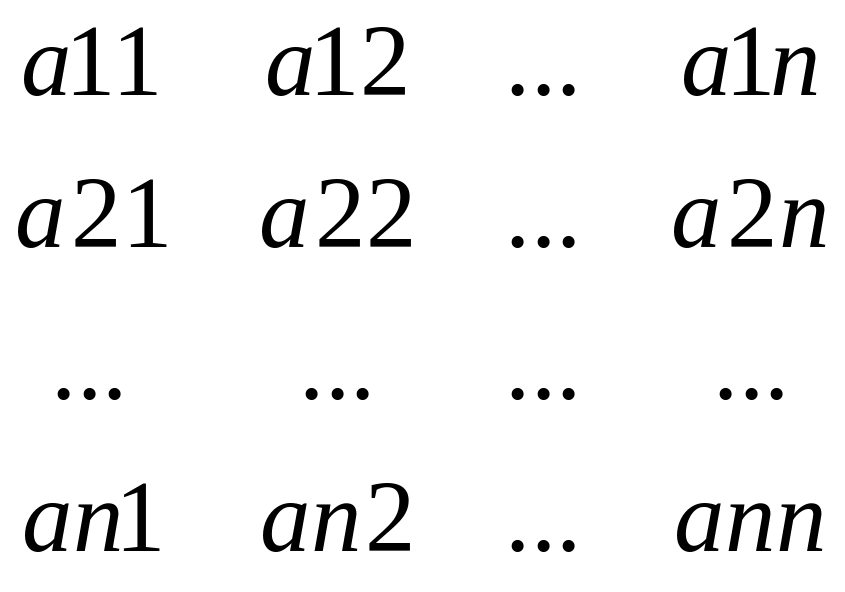

Если в лин.прост-ве L задан базис,то каждому лин.оператору отвеч.опред.квадр.матрица порядка n и,наоборот,каждой такой матр.отвечает опр.лин.оп-р. Матрица Аφ назыв.матрицей лин.оп-ра φ. Для каждого лин.оп-ра φ и нулевого век-ра 0 из L φ(0)=0. При этом,если φ(0)=0 только при х=0,то оп-р φ назыв.невырожденным. если есть такой вектор х 0,что φ(0)=0, то оп-р φ-вырожденный. Пусть Аφ=(а_ij)-матр.лин оп-ра φ. Рассм.сис-му лин.однородных ур-ний:

а11х1+а12х2+…+а1nхn=0

а21х1+а22х2+…+а2nхn=0

…………………………….

а n1х1+аn2х2+…+аnnхn=0.

Для сущ-ния ненулевого решения этой сис-мы необх.и дост.,чтобы оп-ль матр. Аφ был равен 0. Чтобы оп-р φ был невырожденным,необх.и дост.,чтобы опр-ль матр. Аφ этого оп-ра(в любом базисе)был отличен от 0. Матр,опр-ль которой отличен от 0,назыв. невырожденной матрицей.

Пример. Пусть в φ(а) в трехмерн.пр-ве - вектор,симметр. вектору а относит. пл-ти хОу. Линейность этого преобразования очевидна. При этом φ(е1)=е1, φ(е2)=е2, φ(е3)=-е3,и матр.преобразования имеет вид Аφ=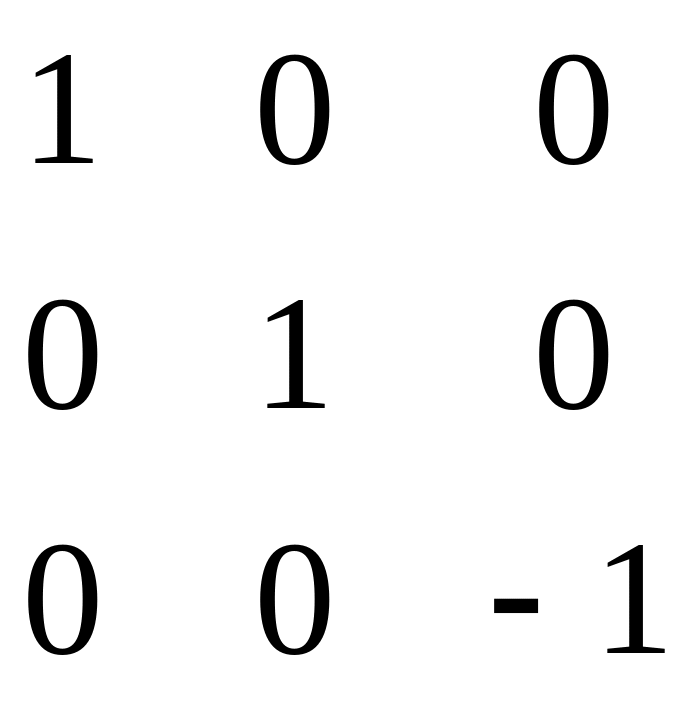

Действия над лин.оп-рами:

1. сложение лин.операторов. Если φ и ψ-два лин.оп-ра в лин.прост-ве L,то их суммой φ+ψ назыв. оп-р τ,опр-емый равенством τ(х)= φ(х)+ψ(х) для любого х, принад-щего L. Если лин. оп-ры φ и ψ имеют в некот. базисе матрицы Аφ и Аψ,то А_φ+ψ=Аφ+Аψ.

Св-ва: 1. φ + ψ= ψ+φ 2. (φ + ψ)+τ = φ+ (ψ+ τ). 3. φ+0= φ для любого φ. И др.

2. умножение лин.оп-ра на число.

Если φ—лин.оп-р в прост-ве L и λ R,то произв-нием φ на λ назыв. оп-р λ* φ, определ-емый как (λ* φ)(х)=λ(φ(х)) для каждого в-ра х L. (λ* φ)-лин.оп-р и А_{λ* φ}= λ*Аφ.

Справдливы след.тож-ва: 1. 1* φ= φ, 0* φ=0, (-1)* φ=- φ 2.α*(β*φ)=(αβ)*φ, (α+β)*φ=α*φ+β*φ, α*(φ+ψ)=α*φ+α*ψ

3) Произ-нием φψ опер-ров φ и ψ назыв. оп-р τ такой,что τ(х)

= φ(ψ(х)) для каждого х L. Произ-ние лин.оп-ров тоже будет лин.оп-ром.

1. (φψ)(х+у)=φ(ψ(х+у))=φ(ψ(х)+ψ(у))=φ(ψ(х))+φ(ψ(у))=(φψ)(х)+(φψ)(у)

2. (φψ)(λх)=φ(ψ(λх))=φ(λ*ψ)(х)=λ*φ(ψ)(х)=λ(φψ)(х).

14.Собственные вектора и собственные значения линейного оператора. Характеристический многочлен и его свойства. Теорема о том, что характеристический многочлен линейного оператора не зависит от выбора базиса.

В-р х 0 назыв.собст.вектором лин. оп-ра φ,если найдется такое число λо, что φ(х)=λо*х. Число λо назыв. соотв-ющим вектору х собственным знач.оп-ра φ матрицы Аφ.

Найдем собствен.значения и собст.векторы лин.оп-ра.

Выберем в пр-ве L произв.базис e1,e2,…,en, и пусть х= х1e1+х2e2+…+хnen, а Аφ=(а_ij)-матрица оп-ра φ в этом базисе. Тогда φ(х)= (а11x1+а12x2+…+а1nxn)e1+( а21x1+а22x2+…+а2nxn)e2+…+(аn1x1+аn2x2+…+аnnxn)en= λо*( х1e1+х2e2+…+хnen), откуда ввиду единственности разложения вектора φ(х) по базису e1,e2,…,en имеем:

( а11- λо)x1+а12x2+…+а1nxn=0

а21x1+(а22- λо)x2+…+а2nxn=0

………………………………….

аn1x1+аn2x2+…+(аnn-λо)xn=0.

Для сущ-ния ненулевого решения этой однородной сис-мы необх.и дост.,чтобы ее оп-ль был равен 0.

а 11- λо а12 … а1n

а21 а22- λо…. c2n

……………………….

аn1 аn2 аnn-λо

Левая часть посл.рав-ва совпадает со значением при λ=λо оп-ля det(Aφ-λ*E) матрицы Аφ-λ*Е,который явл. Многочленом относ-но λ степени n. Коэф-ты этого многочлена f(λ), называемого характерестическим многочленом матр. Аφ,принадлежат полю действ.чисел. Т.о., каждое собств.зн-ние лин. оп-ра φ явл. корнем его характеристического многочлена.

Теорема Характеристический многочлен лин.оп-ра не зависит от выбора базиса.

Док-во. Пусть f(λ) = det(Aφ-λ*E) – харектер.многочлен оп-ра φ в базисе e1,e2,…,en. Предположим,что базис e’1,…,e’n получ.из старого при помощи матр. С. Тогда характ.многочлен f’(λ) оп-ра φ в базисе e’1,…,e’n равен f’(λ)=det(C^-1AφC-λ*E)=

det(C^-1AφC- C^-1λ*EC)=det(C^-1(Aφ-λ*E)C)=det(C^-1 )*det(Aφ- λ*E)*det(C)= det(Aφ-λ*E)=f(λ)

Пусть f(λ)=(-1)ⁿ λⁿ+(-1)^n-1α1λ ^n-1+..+ α_n –характ.многочлен оп-ра φ. Легко видеть,что α1 равно следу матр. Аφ, а α_n =f(0)=det(Аφ). Поэтому для того,чтобы оп-р φ был неврожденным,необх.и дост.,чтобы f(0)было отлично от 0,т.е. чтобы оп-р φ не имел нулевых собств. значений. Для тождественного(нулевого) оп-ра все ненулевые век-ры прост-ва явл.собст. с собств. зн-ями,равными единице(нулю).