
- •16. Кратные, криволинейные, поверхностные интегралы.
- •16.1. Двойной интеграл.
- •16.1.3. Свойства двойного интеграла.
- •Интеграл от единичной функции по области равен площади этой области: .
- •Теоремы об оценке интеграла.
- •Вычисление двойного интеграла. Двукратный (повторный) интеграл.
- •16.1.5. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •16.1.6. Задачи на двойной интеграл.
- •16.1.7. Приложения двойного интеграла.
16. Кратные, криволинейные, поверхностные интегралы.
16.1. Двойной интеграл.
 16.1.1.
Определение двойного интеграла.
Теорема
существования двойного интеграла. Пусть
на плоскости Oxy
задана ограниченная замкнутая область
D
с кусочно-гладкой границей, и пусть на
области D
определена функция
16.1.1.
Определение двойного интеграла.
Теорема
существования двойного интеграла. Пусть
на плоскости Oxy
задана ограниченная замкнутая область
D
с кусочно-гладкой границей, и пусть на
области D
определена функция
![]() .
.
Разобьём область
D
произвольным образом на
![]() подобластей
подобластей
![]() (не имеющих общих внутренних точек).
Символом
(не имеющих общих внутренних точек).
Символом
![]() будем обозначать площадь области
будем обозначать площадь области
![]() ;
символом
;
символом
![]() здесь и дальше будет обозначаться
наибольшее расстояние между двумя
точками, принадлежащими области D:
здесь и дальше будет обозначаться
наибольшее расстояние между двумя
точками, принадлежащими области D:
![]() ;
;
символом
![]() обозначим наибольший из диаметров
областей
:
обозначим наибольший из диаметров
областей
:
![]() .
.
В каждой из
подобластей
![]() выберем произвольную точку
выберем произвольную точку
![]() ,
вычислим в этой точке значение функции
,
вычислим в этой точке значение функции
![]() ,
и составим интегральную сумму
,
и составим интегральную сумму
![]() .
.
Если существует
предел последовательности интегральных
сумм при
![]() ,
не зависящий ни от способа разбиения
области D
на подобласти
,
ни от выбора точек
,
не зависящий ни от способа разбиения
области D
на подобласти
,
ни от выбора точек
![]() ,
то функция
называется интегрируемой по области
D,
а значение этого предела называется
двойным интегралом от функции
по области D
и обозначается
,
то функция
называется интегрируемой по области
D,
а значение этого предела называется
двойным интегралом от функции
по области D
и обозначается
![]() .
.
Если расписать
значение
![]() через координаты точки
через координаты точки
![]() ,
и представить
,
и представить
![]() как
как
![]() ,
получим другое обозначение двойного
интеграла:
,
получим другое обозначение двойного
интеграла:
![]() .
Итак, кратко,
.
Итак, кратко,
![]() .
.
Теорема существования двойного интеграла. Если подынтегральная функция непрерывна на области D, то она интегрируема по этой области.
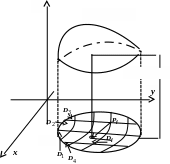
16.1.2. Геометрический
смысл двойного интеграла. Геометрический
смысл каждого слагаемого интегральной
суммы: если
![]() ,
то
,
то
![]() - объём прямого цилиндра с основанием
высоты
- объём прямого цилиндра с основанием
высоты
![]() ;
вся интегральная сумма
- сумма объёмов таких цилиндров, т.е.
объём некоторого ступенчатого тела
(высота ступеньки, расположенной над
подобластью
,
равна
).
Когда
,
это ступенчатое тело становится всё
ближе к изображенному на рисунке телу,
ограниченному снизу областью
;
вся интегральная сумма
- сумма объёмов таких цилиндров, т.е.
объём некоторого ступенчатого тела
(высота ступеньки, расположенной над
подобластью
,
равна
).
Когда
,
это ступенчатое тело становится всё
ближе к изображенному на рисунке телу,
ограниченному снизу областью
![]() ,
сверху - поверхностью
,
сверху - поверхностью
![]() ,
с цилиндрической боковой поверхностью,
направляющей которой является граница
области
,
а образующие параллельны оси
,
с цилиндрической боковой поверхностью,
направляющей которой является граница
области
,
а образующие параллельны оси
![]() .
Двойной интеграл
равен объёму этого тела.
.
Двойной интеграл
равен объёму этого тела.
16.1.3. Свойства двойного интеграла.
16.1.3.1. Линейность. Если функции ,
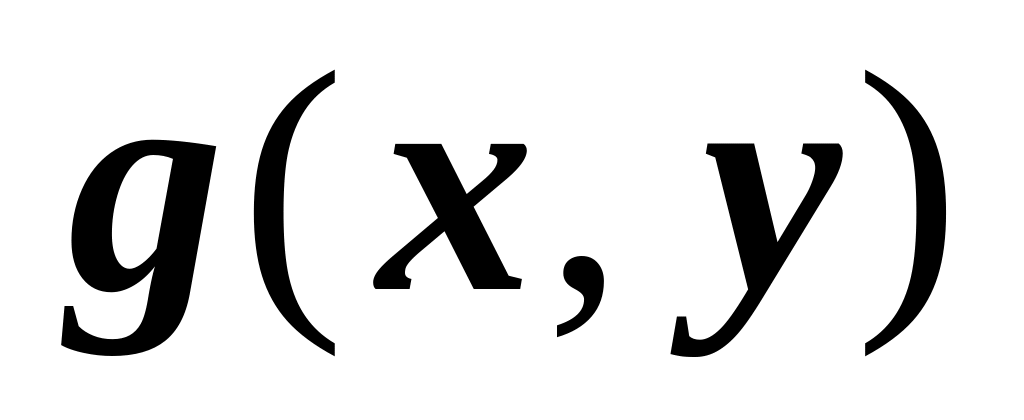 интегрируемы по области
,
то их линейная комбинация
интегрируемы по области
,
то их линейная комбинация
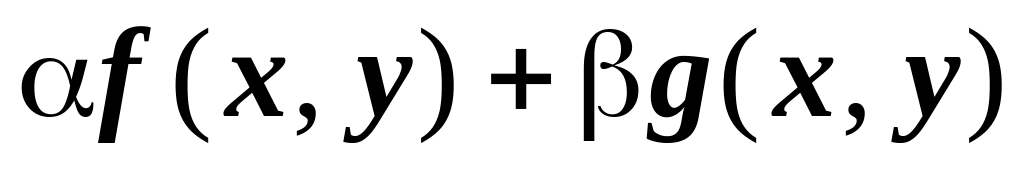 тоже интегрируема по области
,
и
тоже интегрируема по области
,
и

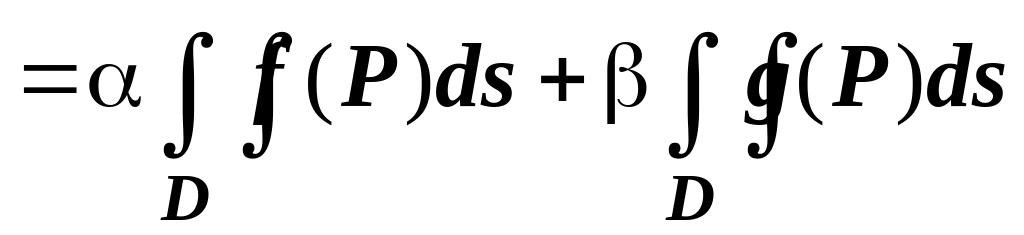 .
.
Док-во. Для
интегральных сумм справедливо равенство
![]()
![]() .
Переходя к пределу при
и пользуясь свойствами пределов,
рассмотренными в разделе 4.4.6.
Арифметические действия с пределами
(конкретно, свойствами 4.4.10.1 и 4.4.10.2),
получим требуемое равенство.
.
Переходя к пределу при
и пользуясь свойствами пределов,
рассмотренными в разделе 4.4.6.
Арифметические действия с пределами
(конкретно, свойствами 4.4.10.1 и 4.4.10.2),
получим требуемое равенство.
16.1.3.2. А ддитивность.
Если область
является объединением двух областей
ддитивность.
Если область
является объединением двух областей
![]() и
и
![]() ,
не имеющих общих внутренних точек, то
,
не имеющих общих внутренних точек, то
![]() .
.
Док-во. Пусть
область
разбита на подобласти
![]() ,
область
разбита на подобласти
,
область
разбита на подобласти
![]() .
Тогда объединение этих разбиений даст
разбиение области
:
.
Тогда объединение этих разбиений даст
разбиение области
:
![]() на
на
![]() подобластей. Интегральная сумма по
области
равна сумме сумм по областям
и
:
подобластей. Интегральная сумма по
области
равна сумме сумм по областям
и
:
 .
Как и в предыдущем случае, переходя к
пределу при
.
Как и в предыдущем случае, переходя к
пределу при
![]() ,
получим требуемое равенство.
,
получим требуемое равенство.
Интеграл от единичной функции по области равен площади этой области: .
Док-во: Для
любого разбиения
![]() ,
т.е. не зависит ни от разбиения, ни от
выбора точек
.
Предел постоянной равен этой постоянной,
поэтому
,
т.е. не зависит ни от разбиения, ни от
выбора точек
.
Предел постоянной равен этой постоянной,
поэтому
![]() .
.
16.1.3.4.
Интегрирование
неравенств.
Если в любой точке
![]() выполняется неравенство
выполняется неравенство
![]() ,
и функции
,
и функции
![]() интегрируемы по области
,
то
интегрируемы по области
,
то
![]() .
.
Док-во.
В любой точке
![]() выполняется неравенство
выполняется неравенство
![]() ,
поэтому
,
поэтому
![]() .
По теореме о переходе к пределу в
неравенствах отсюда следует требуемое
утверждение.
.
По теореме о переходе к пределу в
неравенствах отсюда следует требуемое
утверждение.
