11.6. Возмещение премии и накопление дисконта облигаций

Проблема оценки облигаций существует не только тогда, когда облигация покупается или продается на рынке, но и когда она находится у владельца. В общем случае ее цена изменяется во времени даже в такой крайне редкой ситуации, когда рыночная процентная ставка остается постоянной, и уж тем более, если эта ставка изменяется. С приближением даты погашения увеличивается современная стоимость суммы, получаемой при погашении облигации, одновременно уменьшается современная стоимость будущих поступлений по купонам. Какой бы ни была цена до погашения, в конце срока цена облигации равна номиналу или некоторой заранее фиксированной выкупной цене.

Проследим, к каким изменениям в цене или курсе облигаций приводит ход времени. Для этого вернемся к формуле (11.7) и запишем ее для некоторого момента t после выпуска облигации:

t = l, 2, ..., n,

где K_t — курс в момент t ( после очередной выплаты процентов);

n - t — срок, оставшийся до даты погашения.

Для t = n K_t = 100, так как считаем, что проценты в этот момент уже получены.

Нетрудно установить, что у облигации, купленной с премией, второе слагаемое курса сокращается скорее, чем увеличивается первое. В связи с этим премия и курс в целом уменьшаются с каждым шагом во времени. Такой процесс получил название возмещение премии (amortization).

По определению абсолютный размер премии (дисконта) находится как

E = P - N.

Премия в расчете на курс в момент t составит

e_t = K_t - 100.

На рис. 11.7 и в табл. 11.7 иллюстрируется процесс возмещения премии на примере облигации с условиями: п = 8, g = 8%, i = 6%.

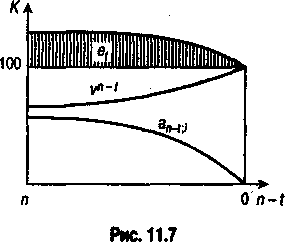
Таблица 11.7

t	100vn-t	100ga8-t;6	Kt	et
0	62,74	49,68	112,42	12,42
1	66,51	44,66	111,17	11,17
2	70,50	39,34	109,83	9,83
...
7	94,34	7,55	101,89	1,89
8	100,00	0	100,00	0

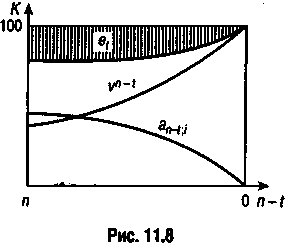
На рис. 11.8 иллюстрируется процесс роста цены за счет накопления дисконта (accumulation). В ходе этого процесса цена и курс облигации увеличиваются во времени, поскольку на каждом шаге во времени рост первого слагаемого перекрывает сокращение второго. Процессы изменения курса рассматривались нами на фоне стабильной рыночной ставки. Однако это условие нереалистично. Действительный курс в связи с изменениями процентной ставки отклоняется от "идеального", динамика которого представлена на рис. 11.7 и 11.8.

11.7. Портфель облигаций

Портфель (набор), охватывающий различные по видам и срокам облигации, также является объектом количественного финансового анализа. Простейший анализ заключается в оценке полной доходности портфеля и средних, характеризующих сроки платежей. Более сложный — в определении оптимальной структуры портфеля, в разработке и проведении такой стратегии при формировании структуры портфеля, которая обеспечивает гарантированный поток платежей (immunization). Последние из названных направлений анализа требуют самостоятельного рассмотрения, которое выходит за рамки настоящей книги.

Доходность портфеля. Данный параметр измеряется в виде годовой ставки сложных процентов. Эта ставка находится с помощью ряда методов. Наиболее точным является решение уравнения, в котором общая стоимость облигаций приравнивается сумме современных величин всех видов платежей.

Величина ∑Q_jP_j характеризует размер портфеля по цене приобретения, ∑S_tv_t — сумма современных величин всех поступлений от облигаций, определенных по искомой ставке i. Здесь

S_t — член потока платежей в момент t;

Q_j — количество облигаций вида j;

p_j — цена приобретения облигаций;

v — дисконтный множитель по ставке i (напомним, что значение i находят с помощью интерполяции или каким-либо итерационным методом).

Приближенные методы заключаются в расчете средних взвешенных ставок помещения (I). Веса определяются двумя способами.

Согласно первому в качестве весов берутся стоимости облигаций по цене приобретения, тогда

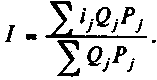(11.29)

Считается, что меньшую погрешность дает взвешивание, когда в качестве весов принимаются произведения показателей D на стоимость облигаций.

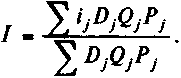(11.30)

Пример 11.16. Портфель, приобретенный за 355 млн. руб., содержит облигации со следующими параметрами:

Облигация	Количество, Qj	Цена, Pj	Номинал, Nj	Срок, nj	Купонный доход, gj	Число выплат в году, pj
А	1000	95	100	5	8%	1
Б	500	120	200	8	-	-
В	2000	100	100	4	9%	2

На основе приведенных данных сформируем поток платежей (табл. 11.8, гр. 2). Для этого найдем размер платежа в конце каждого полугодия. Время в годах здесь: 0,5; 1; 1,5 и т.д. Размер платежа в первом полугодии равен только процентам от облигаций типа В, в конце первого года — сумме процентов по облигациям A и В, в конце четвертого года — сумме процентов и стоимости погашения номинала облигаций типа В.

Таблица 11.8

t	Rt
1	2	3	4	5	6
0,5	9000	0,9622	0,9578	8660	8622
1,0	17000	0,9259	0,9174	15741	15596
1,5	9000	0,8910	0,8787	8019	7909
2,0	17000	0,8573	0,8417	14575	7575
2,5	9000	0,8250	0,8062	7425	7256
3,0	17000	0,7938	0,7722	13495	13127
3,5	9000	0,7638	0,7396	6875	6656
4,0	217000	0,7350	0,7084	159501	153728
5,0	10800	0,6806	0,6499	73503	70192
8,0	100000	0,5403	0,5019	54027	50187
Итого:				361820	346860

Поскольку ожидаемое значение средней ставки помещения находится между 8 и 9%, рассчитаем соответствующие дисконтные множители — гр. 3 и 4. В гр. 5 и 6 приводятся дисконтированные величины членов потоков платежей.

По интерполяционной формуле (11.10), в которой вместо P_k применим сумму цен, находим

I = 8 + (9 - 8) = 8,48%.

Проверка: сумма дисконтированных по этой ставке платежей составит 344 850 руб., дальнейшее уточнение оценки дает i = 8,47%, при этом контрольная сумма равна 355 000.

Пример 11.17. Найдем приближенные показатели доходности портфеля облигаций примера 11.16. Показателем доходности облигаций в виде годовых ставок сложных процентов равны соответственно 9,3; 6,59 и 9%.

Применив приближенную формулу (11.29) (общая стоимость облигаций взята в десятках тыс. руб.), получим

I = = 8,67%.

Ответ заметно отличается от точного (8,47%). Для того чтобы применить формулу 11.30., необходимо найти показатели D для каждого вида облигаций. Определим их по формуле (11.23): 4,2; 8 и 3,47 года. В этом случае для портфеля облигаций получим

I = = 8,34%.

Погрешность в ответе несколько меньше, чем в полученном по формуле (11.29).

Средняя продолжительность платежей портфеля. Для дальнейшего анализа портфеля облигаций нам необходимо установить зависимость между общей средней продолжительностью платежей портфеля в целом и аналогичными характеристиками облигаций, входящих в этот портфель. В связи с этим предварительно рассмотрим условный портфель, состоящий из двух облигаций. Соответственно имеются два потока платежей: R_j и S_j. Каждый из данных потоков характеризуется следующими средними продолжительностями платежей:

Для потока платежей от двух облигаций находим

Отсюда следует, что

Таким образом, средняя продолжительность суммарного потока платежей равна средней взвешенной аналогичных характеристик частных потоков.

Для m частных потоков получим

j = l, 2, ..., m, (11.31)

где h_j — удельный вес цен облигации вида j в сумме цен всех облигации. Удельные веса можно получить на основе не только цен облигаций, но и их курсов. Для облигации k находим

Нетрудно убедиться в том, что найденная выше зависимость справедлива и для модифицированных средних:

Пример 11.18. Найдем для портфеля облигаций примера 11.16 среднюю продолжительность платежей:

D₀ = = 4,43 года.