1. Матрицей называется прямоуг.таблица чисел или буквенных выражений,содержащая n строк и m столбцов.Матрица обозначается большими латинскими буквами А,В,С.

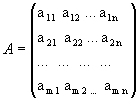
Числа a _{i j}-назыв-ся элементами

Матрицы

i-ая строка

j-ый столбец 

Действия над матрицами:

1.суммирование. Суммой двух матриц А = (a _{i j} ) и B = (b _{i j} ) одного размера называется матрица C = (c _{i j} ) того же размера, элементы которой определяются по формуле c _{i j}= a _{i j} + b _{i j}.

2.умножение на число. Произведением матрицы А на число l называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число l: l A = (l a _{i j} ).

3.умножение 2-ух матриц. Произведением двух матриц А = (a _{i j} ) и B = (b _jk ),называется матрица С = (c _{i k} ), элементы которой определяются по следующему правилу:c_{i k} =a _{i 1} b _{1 k} + a _{i 2} b _{2 k} +... + a _{i m} b _{m k} 

элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.

2. Определитель-это число,которе ставится в соответствии квадратной матрицы по определенному правилу . Порядком определителя назыв-ся число строк(столбцов)квадратичной матрицы. Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Определитель 2-го порядка равен произведению элементов гл.диагонали (диагональ идущая из левого верхнего угла в правый нижний угол) минус произведение элементов побочной диагонали(диагональ идущая из левого нижнего угла в правый верхний)

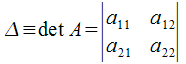
Определитель 3-го порядка можно вычислить 2-мя способами!

1-ый Метод триуг-ка .

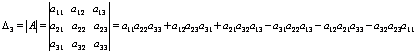
2-ой С помощью разложения по элементам столбца или строки.для этого введем понятие минора

Минором   элемента   матрицы n-го порядка называется определитель матрицы  -го порядка, полученной из матрицы   вычеркиванием   -й строки и  -го столбца.

минором  матрицы   3-го порядка будет: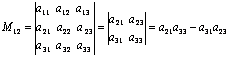 

Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком плюс, если сумма номеров строки и столбца, на пересечении которых стоит этот элемент, четная, и минус, если нечетная.

Алгебраическое дополнение элемента  обозначают  . Таким образом,  .

Знаки, приписываемые минорам определителя 3-го порядка, можно задать таблицей

.

Определитель 3-го порядка можно теперь записать следующим образом:

.

Для определителя 3-го порядка имеет место теорема разложения. Определитель 3-го порядка равен сумме произведений элементов какого –либо ряда определителя на их алгебраические дополнения.

Свойства определителей

Свойство № 1: Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот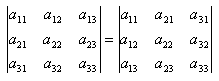

Свойство № 2:

При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:

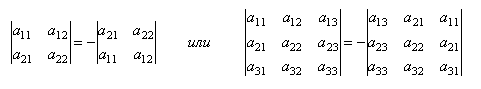
Свойство № 3:

Определитель матрицы, имеющий два одинаковых ряда, равен нулю.

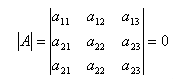
Свойство № 4:

Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.

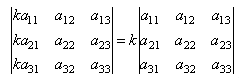
Свойство № 5:

Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.

Свойство № 6:

Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-хопределителей по формуле:

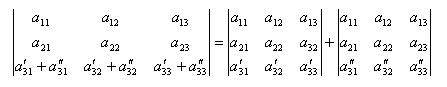
Свойство № 7:

Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

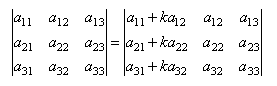
4 Вектор – это направленный отрезок, соединяющий две точки в пространстве или в плоскости. Векторы обычно  обозначаются либо маленькими буквами, либо начальной и конечной точками. Сверху обычно ставят чёрточку.. 

Линейные операции над векторами:

Сложение

Правило треугольника:  следующий способ построения суммы произвольных

в екторов a и b. Надо от конца вектора a отложить вектор равный вектору b. Тогда вектор, начало которого совпадает с началом вектора a, а конец - с концом вектора b, будет суммой векторов a и b.

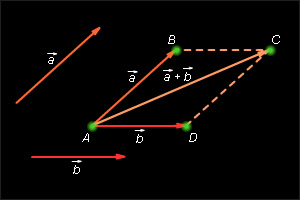
Правило параллелограмма: для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

В ычитание

П равило треугольника. Чтобы найти разность двух векторов, нужно: изобразить их исходящими из одной точки; дополнить чертеж отрезком так. чтобы получился треугольник; придать отрезку направление от вычитаемого к уменьшаемому; этот направленный отрезок и будет вектором разности.

Умножение вектора на число

Произведением вектора   на скаляр (число)   является вектор 

5

Разложение по ортам

а=а_х*i+a_y*j+a_z*k – формула разложения вектора а по базисным векторам i.j.k

С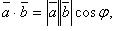 калярное произведение векторов(не нулевых)называется число равное произведению векторов на cos угла между ними

6.

Векторное произведение. Вектор  с называется векторным произведением  векторов а и b, если:

1)       |c| = |a||b|sinφ, где φ – угол между а и b.

2)       c a, c b.

3)       Тройка векторов abc является правой.

Длина вектора численно равна площади параллелограмма, построенного на векторах и как на сторонах (это геометрический смысл векторного произведения).

С мешанное произведение 3-ех векторов – называется скалярное произведение векторного произведения а и b на с. Результат смешанного произведения есть число(скалярное)

Геометрический смысл: заключается в том что модуль смешан.произведения=объему параллелепипеда ,построенного на векторах аbс

7. Общее уравнение прямой

Уравнение прямой, проходящей через две точки

Уравнение прямой с угловым коэффициентом

Уравнение прямой в отрезках

Прямая линия, пересекающая ось Ox в точке   и ось Oy в точке  :

8

Уравнение плоскости в пространстве :

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0. Уравн-е плоскости ,проходящей ч/з данную точку ,перпендик-но нормальному сектору этой пл-ти.

У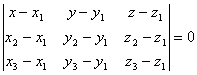 равнение плоскости, проходящей через три точки:

Взаимное расположение плоскостей в пространстве :

Для расположения двух плоскостей в пространстве возможны два случая:

1) Две плоскости имеют хотя бы одну общую точку, тогда по аксиоме пересечения плоскостей их пересечение - есть прямая; такие плоскости называются пересекающимися.

2) Две плоскости не имеют общих точек; такие плоскости называются параллельными.

Расстояние от точки до плоскости

Расстояние от произвольной точки М₀(х₀, у₀, z₀)  до плоскости Ах+Ву+Сz+D=0 равно:

• 9. Каноническое уравнение плоскости в пространстве:

Аx+By+Cz+D=0, где D = -Ax₀-By₀-Cz₀.

• Параметрические уравнения прямой в пространстве:

 

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A₁ x + B₁ y + C₁ z + D₁ = 0, A₂ x + B₂ y + C₂ z + D₂ = 0;              

2) двумя своими точками M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), тогда прямая, через них проходящая, задается уравнениями:

= ;                                       

3) точкой M₁(x₁, y₁, z₁), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

.                                        

Уравнения (3.4) называются каноническими уравнениями прямой.

Вектор a называется направляющим вектором прямой.

Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:

x = x₁ +mt, y = y₁ + nt, z = z₁ + рt.                              

Взаимное расположение прямых в пространстве :

Возможны четыре различных случая расположения двух прямых в пространстве:

– прямые скрещивающиеся, т.е. не лежат в одной плоскости;

– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;

– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;

– прямые совпадают.

10.

Кривые 2го порядка

Э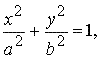 ллипс

Гипербола

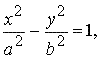
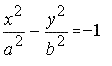
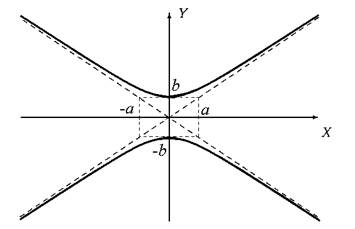
Парабола

y² = 2 px

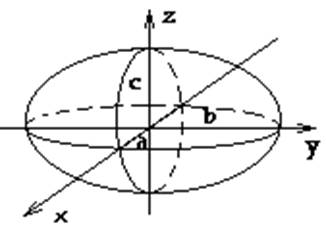1 1.

Э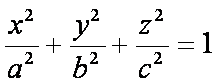 ллипсоид

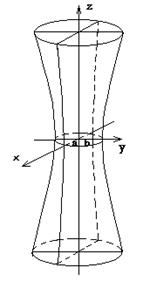
Однополосный гиперболоид

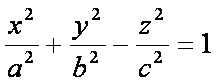
Д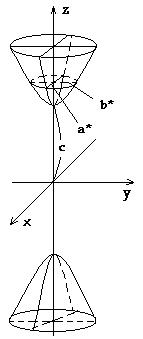 вуполостный гиперболоид.

Э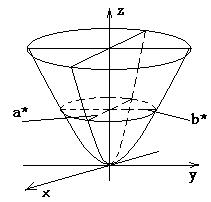 ллиптический параболоид.

Г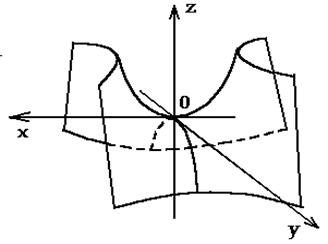 иперболический параболоид

      

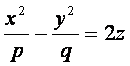
К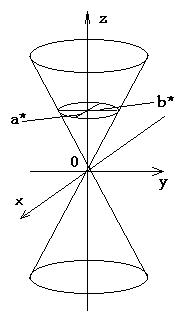 онус второго порядка

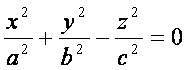
12

Число   называется пределом числовой последовательности  , если последовательность   является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

В случае, если у числовой последовательности существует предел в виде вещественного числа  , её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равенминус бесконечности.

Частичный предел последовательности — это предел одной из её подпоследовательностей.

Верхний предел последовательности — это наибольшая из её предельных точек.

Нижний предел последовательности — это наименьшая из её предельных точек.

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

13.

• П 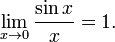ервый замечательный предел:

• В 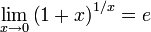торой замечательный предел:

14.

15.

Неопределенности типа 

Пусть заданы две функции f (x) и g (x), такие, что

В этом случае говорят, что функция   имеет неопределенность типа   в точке x = a. Чтобы найти предел при x = a когда функция   содержит неопределенность  , нужно разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю. 

Неопределенности типа 

Пусть две функции f (x) и g (x) обладают свойством

где a является действительным числом, либо стремится к + ∞ или − ∞. Говорят, что в этом случае функция   имеет в точке a неопределенность типа  . Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени. 

16.

17.

П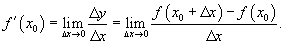 роизводная фун-ии назыв-ся предел отношении приращение функции к приращению аргумента при стремящемся аргумента к 0,если этот предел сущ-т и конечен.

Г еометрическ.смысл производной. Производная функции y = f (x) в т.х=tga угла наклона касательной к графику функции в т.х

Производная от координаты по времени есть скорость. В этом состоит механический смысл производной.

v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смысл производной. Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).

Основные правила дифференцирования

* Функция f(x) называется дифференцируемой в точке x0, если она имеет производную в этой точке.