30.Распределение выборочных средних. Центральная предельная теорема, стандартная ошибка средней.

Центральная предельная теорема (Ц.П.Т.) — класс теорем в теории вероятностей, утверждающих, что сумма большого количества независимых случайных величин имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях являются суммами нескольких случайных факторов, центральные предельные теоремы обосновывают популярность нормального распределения. Классическая формулировка Ц.П.Т.

Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние μ и σ², соответственно. Пусть . Тогда

по распределению при .

Обозначив символом выборочное среднее первых n величин, то есть , мы можем переписать результат центральной предельной теоремы в следующем виде:

по распределению при .

• классическая центральная предельная теорема утверждает, что сумма n независимых одинаково распределённых случайных величин имеет распределение, близкое к N(nμ,nσ²). Эквивалентно, имеет распределение близкое к N(μ,σ² / n).

• Так как функция распределения стандартного нормального распределения непрерывна, сходимость к этому распределению эквивалентна поточечной сходимости функций распределения к функции распределения стандартного нормального распределения. Положив , получаем 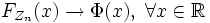, где Φ(x) — функция распределения стандартного нормального распределения.

• Центральная предельная теорема в классической формулировке доказывается методом характеристических функций (теорема Леви о непрерывности).

Ц.П.Т. Ляпунова

Пусть выполнены базовые предположения Ц.П.Т. Линдеберга. Пусть случайные величины {X_i} имеют конечный третий момент. Тогда определена последовательность

. Если предел

(условие Ляпунова),

то

по распределению при .

31.Доверительные интервалы для средней при больших выборках. Поправка на конечность генеральной совокупности.

Для построения доверит интервалов для параметров генеральных совокупностей могут быть реализованы два подхода,основанных на значении точного(при данном объеме выборки n) или асимптотического (при n→∞) распределения выборочных характеристик или некоторых функций от них. Первый подход-для построения интервальных оценок параметро для малых выборок, второй-для больших выборок. Теорема. Вероятность того,что отклонение выборочной средней(или доли) от генеральной средней(или доли) не превзойдет число ∆>0 (по абсолютной величине) равна: , где . ,где

32.Доверительные интервалы для средней при малых выборках. T-распределение

Стьюдента, степень свободы. Поправка на конечность генеральной совокупности.

Задача построения доверительного интервала для генеральной средней может быть решена,если в генеральной совокупности рассматриваемый признак имеет нормальное распределение. Теорема.Если признак(случайная величина) Х имеет нормальный закон распределения с параметрами М(Х)=х₀, , т.е. ,то выборочная средняя х пи любом n(а не только при n→∞) имеет нормальный закон распределения . Распределением Стьюдента(или t-распределением) называется распределение случайной величины , где Z-случайная величина,распределенная по стандартному нормальному закону, т е N(0;1). -независимая от Z случайная величина,имеющая -распределение с k степенями свободы. При k→ t-распределение приближается к нормальному.При k>30 можно считать t-распределение приближенно нормальным. Математическое ожидание случайной величины,имеющей t-распределение, в силу симметрии ее кривой распределения равно нулю, а ее дисперсия равна k/(k-2), т.е. M(t)=0, D(t)=k/(k-2)