6. Розвязування системи матричним методом

Розвязати систему матричним методом

х₁ + 2х₂ +х₃=4

2х₁- х₂+ 3х₃=5

3х₁+х₂ - х₃=-1

7. Ранг матриці та способи його обчислення

Будемо розглядати матрицю A порядку m+n з дійсними елементами

Рядки цієї матриці можна розглядати як n- вимірні вектори a₁, a₂,… a_m з дійсними координатами (елементи простору Rⁿ). Ранг системи векторів a₁, a₂,… a_m називається горизонтальним рангом матриці (або рангом матриці за рядками) і позначається .r_r(A).

Стовпчики матриці A можна розглядати як m- вимірні вектори b₁, b₂,…b_n

з дійсними координатами (елементи простору R^m). Ранг системи векторів b₁, b₂,…b_n називається вертикальним рангом матриці A (або рангом матриці A за стовпчиками) і позначається r_b(A).

Мінором матриці A порядку k (k≤m,k≤n) називається визначник, побудований на перетині будь-яких k рядків і k стовпчиків матриці.

В матриці A візьмемо всі мінори, які не дорівнюють нулю. Серед них виберемо мінор найвищого порядку. Порядок цього мінору будемо називати рангом матриці A за мінорами і позначати r_m(A). Якщо всі елементи матриці дорівнюють нулю, ранг матриці за мінорами будемо вважати рівним нулю.

Ранг матриці можна знайти так. Якщо всі мінори першого порядку (елементи матриці) дорівнюють нулю, то r = 0. Якщо хоч один з мінорів першого порядку відмінний від нуля, а всі мінори другого по­рядку дорівнюють нулю, то r = 1. У випадку, коли є мінор другого по­рядку, відмінний від нуля, досліджуємо мінори третього порядку. Так продовжуємо доти, поки не станеться одне з двох: або всі мінори по­рядку k дорівнюють нулю, або мінорів порядку k не існує, тоді r = k –1

Вказаний метод знаходження рангу матриці не завжди зручний, тому що пов'язаний з обчисленням значного числа визначників. Простіший метод грунтується на тому, що ранг матриці не змінюється, якщо над матрицею виконати так звані елементарні перетворення, а саме :

а) переставити місцями два рядки (стовпці);

б) помножити кожен елемент рядка (стовпця) на один і той самий відмінний від нуля множник;

в) додати до елементів рядка (стовпця) відповідні елементи другого рядка (стовпця), помножені на одне і те саме число.

8. Теорема Кронекера- Капеллі.Теорема: система лінійних алгебрарічних рівнянь сумісна тоді, і тількі тоді, коли ранг основної матриці дорівнює рангу розширенної матриці.

9. Вектор.Лінійні операції з векторами.

Вектор – впорядкована пара точок(М,N),перша з яких називається початком векторав,друга-його кінцем. Вектор з початком М та кінцем N позн.MN(з рисочкою) і зображається відрізком,на якому стрілкою позначається напрям від М до N. Якщо ж неістотно,які саме початок і кінець вектора ,його позначають однією буквою,наприклад , а і б (з рискою) тощо. відстань між М та N називається довжиною або модулем вектора . Дії з векторами виконуються за правилами:

1. Додавання: = (а_х + b_х, а_у + b_у, а_z + b_z).

2. Множення вектора на число   R: .

10. Скалярний добуток векторів та його властивості.

Скалярним добутком двох векторів і називається добуток довжин цих векторів на косинус кута, утвореного векторами. Якщо хоча б один із векторів дорівнює нулю, то кут між векторами не визначений і за означенням скалярний добуток дорівнює нулю.

Скалярний добуток двох векторів дорівнює добутку довжини одного з них на проекцію іншого на напрям першого.

1. .

2. .

3. .

4. .

5. якщо і навпаки, якщо .

11. Пряма на площині.

Рис. 2.14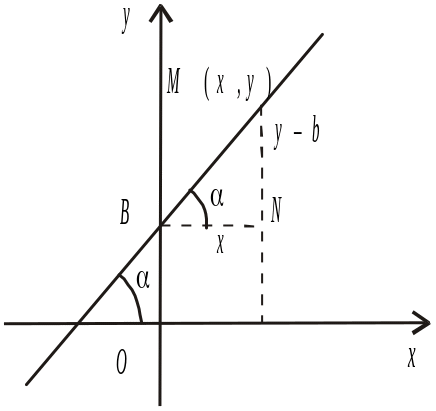

Нехай задано деяку пряму знайдемо її рівняння.

Точка М (х, у) лежить на прямій тоді і тільки тоді, коли виконується умова .Позначимо tg  = k і назвемо цю величину кутовим коефіцієнтом прямої лінії. Тоді, враховуючи, що NM = y – b, BN = x, маємо рівняння прямої з кутовим коефіцієнтом у = kx + b. (2.14)

Нехай деяка точка М₁ (х₁, у₁) належить заданій прямій, тоді у₁ = kx₁ + b. Знайдемо з цього рівняння значення b і, підставивши його в рівняння прямої дістанемо:у – у₁ = k (х – х₁) (2.15)

— рівняння прямої, що проходить через задану точку М₁ (х₁, у₁).

Нехай ще одна точка М₂ (х₂, у₂) також належить заданій прямій, тоді з означення лінії маємо:у₂ – у₁ = k (x₂ – x₁).

Знайдемо значення k з останнього співвідношення і, підставивши його в рівнянняпрямої, дістанемо: . Останнє рівняння називається рівнянням прямої, що проходить через дві задані точки.

12. Відстань від точки до прямої

Нехай задано деяку точку М₀ (х₀, у₀) і пряму l: Ах + Ву + С = 0. Пересвідчимось, що М₀ не лежить на прямій, Ах₀ + Ву₀ + С  0, тоді відстань від точки М₀ (х₀, у₀) до прямої Ах + Ву + С = 0 можна знайти за формулою: .

13. Еліпс,гіпербола,парабола.

Еліпс. Означення. Множина точок площини, для яких сума відстаней від двох заданих точок, що називаються фокусами, є величина стала й така, що дорівнює 2а і більша, ніж відстань між фокусами, називається еліпсом.Тоді канонічне рівняння еліпса, де b² = а² – с².

Гіпербола. Означення. Множина точок площини, для яких модуль різниці відстаней від двох заданих точок, що називаються фокусами, є величиною сталою, яка дорівнює 2а і менша за відстань між фокусами, називається гіперболою.

Скористаємось рис. 2.17, з якого бачимо, що точки F₁ (– c, 0) і F₂ (c, 0) — фокуси гіперболи, точка М (х, у) — точка визначеної множини. Тоді .

Канонічне рівняння гіперболи має вигляд: , де b² = c² – a².Парабола. Означення. Множина то­чок площини, що містяться на одна- ковій відстані від даної точки фокуса і даної прямої, яка не проходить че- рез фокус і називається директрисою, є парабола.

За означенням r = d, отже (див. рис. 2.18): або у² = 2рх— канонічне рівняння параболи, коли  = 1.

14. Площина. Пряма у просторі.

Нехай задано прямокутну систему координат Охуz, площину , вектор , який має координати , і точку , яка належить площині

Точка М (х, у, z) — довільна точка площини. Ця точка належить площині лише в тому разі, коли вектори і взаємно перпендикулярні.Умова перпендикулярності векторів

. (2.25)

Останній вираз можна розглядати як векторне рівняння площини. Координати вектора дорівнюють відповідно х – х₀, у – у₀, z – z₀. Записавши вираз (2.25) у розгорнутому вигляді, дістанемо рівняння площини, що проходить через задану точку:

(2.26)

Розкривши дужки в і позначивши , дістанемо загальне рівняння площини:

Пряму у просторі можна задати як лінію перетину двох площин у прямокутній системі координат:

(2.31)

Зрозуміло, що ці площини мають бути непаралельними, тобто їхні нормальні вектори , — не колінеарні. Система (2.31) називається загальним рівнянням прямої. Дістанемо ще деякі форми рівняння прямої.

Канонічне рівняння прямої. Нехай у системі координат Охуz задано пряму l і ненульовий вектор , колінеарний цій прямій. Точка належить прямій, а напрямний вектор . Тоді довільна точка М (х, у, z) лежатиме на прямій тоді і тільки тоді, коли вектори і колінеарні:

. (2.32)

Рівняння називається канонічним рівнянням прямої у просторі.

Рівняння прямої, що проходить через дві задані точки.

Нехай дві точки і належать прямій у просторі. Тоді вектор можна розглядати як напрямний вектор прямої. Замінюючи ним вектор у рівнянні , дістанемо шукане рівняння прямої у просторі

15. Поверхні другого порядку.

Поверхнею другого порядку називається множина точок, прямокутні координати яких задовольняють рівняння виду ах²+by²+cz²+dxy+exz+fyz+gx+hy+kz+l=0, (1)

де принаймні один з коефіцієнтів а, b, c, d, e, f відмінний від нуля.

Рівняння(1) називається загальним рівнянням поверхні другого порядку.

Поверхня другого порядку як геометричний об’єкт не змінюється, якщо він заданої прямокутної системи координат перейти до іншої. При цьому рівняння і рівняння, знайдене після перетворення координат, будуть еквівалентні.

Можна довести, що існує система координат, в якій рівняння має найпростіший (або канонічний вигляд.

До поверхонь другого порядку належать, зокрема, циліндричні та конічні поверхні, поверхні обертання, сфера, еліпсоїд, одно порожнинний та двопорожнинний гіперболоїди, еліптичний та гіперболічний параболоїди. Розглянемо ці поверхні та їхні канонічні рівняння