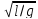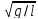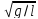- •60. Остается ли момент инерции физического маятника одинаковым относительно осей, проходящих через разные точки подвеса? Почему?
- •63Запишите и объясните физический смысл уравнения неразрывности
- •66. Как измерить среднюю скорость в сечении канала переменного сечения?
- •68. С помощью манометрических трубок в лабораторной работе №6 какое статическое давление вы измеряли? Абсолютное давление или избыточное над атмосферным давлением?
- •69. Вычислите давление столба воды высотой в 1 метр в Паскалях.
- •70. Какие законы сохранения использованы в лабораторной работе №10 ?
- •71) Дайте формулировку закона сохранения механической энергии.
- •73) Что называется моментом импульса? Как определить его направление?
- •76. Что такое вязкость? Дать определение вязкости, указать единицу измерения в си.
- •77. От каких величин зависит вязкость жидкости?
- •78. Какие силы действуют на шар, находящийся в жидкости , в Лабе №11?
- •80. Каким образом можно было бы в Лабе №14 учесть тот факт, что блок обладает массой?
- •85. Как в Лабе №11 влияет на движение шарика его диаметр и диаметр цилиндра , в котором он падает?
- •88) Записать формулу для тангенциального ускорения, раскрыть его физический смысл, указать направление.
- •89) Записать формулу для нормального ускорения, раскрыть его физический смысл, указать направление.
|
1.Дайте определение абсолютной и относительной погрешности. Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Погрешность делится на 2 вида: на абсолютную и относительную погрешности. Абсолютная погрешность: Допустим, что истинное значение некоторой величины есть х0 . Измеряя эту величину, как правило, получают результат, отличный от х0 . Если измерение выполняется неоднократно, то результаты измерений не только отличаются от х0 , но в большинстве случаев различны и между собой. Обозначим результаты измерений х1, х2, х3, …, хп , Тогда разность хi =хi - х0, где i=1,2, …, п , (1.1) называется абсолютной погрешностью измерения. Она выражена в единицах измеряемой величины. Относительная
погрешность: Для оценки точности
эксперимента рассчитывают относительную
погрешность эксперимента. Относительная
погрешность – это погрешность,
выраженная в долях истинного значения
измеренной величины:
|
10.Как найти среднюю квадратичную погрешность отдельного измерения? Методы
обработки результатов прямых измерений,
содержащих случайные погрешности.
Пусть в одних и тех же условиях
проделано N измерений и х(i) – результат
i-го измерения. Наиболее вероятное
значение измеряемый величины – ее
среднеарифметическое значение:
|
|
|
2. Как классифицируются погрешности по свойствам? Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. При классификации погрешностей по их свойствам различают погрешности систематические, случайные и промахи. Систематической погрешностью измерения называется составляющая погрешности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Например, шкала измерительной линейки неравномерна, капилляр термометра имеет в различных участках различный диаметр, весы неравноплечные, стрелка амперметра при отсутствии тока не стоит на нуле и прочие. Эти погрешности, как правило, можно учесть, а поэтому устранить введением поправки к измеренному значению (учесть деление, на котором стоит стрелка амперметра при отсутствии тока и каждый раз вычитать его из показаний прибора). Систематическую погрешность измерения экспериментально можно обнаружить либо сопоставлением данного результата с результатом измерения этой же величины, но полученным другим методом, либо путем использования более точных средств измерений. Однако обычно систематические погрешности оценивают путем теоретического анализа условий измерения, основываясь на известных свойствах средств измерений. Промахи – следствие неправильных действий экспериментатора. Это, например, описка при записи результатов наблюдения, неправильно снятое показание прибора и т.д. При обнаружении промахов их исключают из расчетов. Случайные погрешности – погрешности, изменяющиеся случайным образом. При этом различия между результатами отдельных измерений индивидуально непредсказуемы, а закономерности проявляются лишь при значительном числе измерений.
|
5,Какому _ из двух соответствуют более доброкачественные измерения? 2 является дисперсией, - характеризует разброс измерений относительно среднеарифметического значения и называется стандартным отклонением или среднеквадратичной погрешностью.
Рис.
1.3.
Кривые
распределения Гаусса для различных
значений
1=10,
2=20
и 3=30.
На рис. 1.3. изображены кривые распределения, соответствующие различным . Из этого рисунка видно, что при малом кривая уже, а максимум выше, что соответствует более доброкачественным измерениям. На практике чаще бывает необходимо определить погрешность среднего арифметического. Пусть х1, х2, …, хi, …, хп – результаты отдельных измерений, причем каждое из них характеризуется одной и той же дисперсией. Среднее арифметическое ряда измерений определяется по формуле:
Аналогично
|
|
|
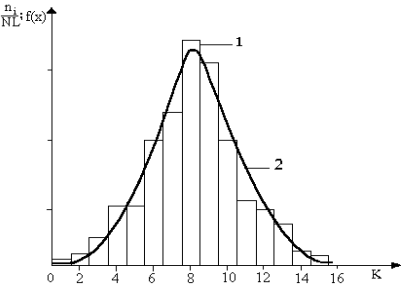
3. Какими свойствами обладает нормальное распределение случайных погрешностей? Методы
обработки результатов прямых измерений,
содержащих случайные погрешности.
Пусть в одних и тех же условиях проделано
N
измерений
и хi
– результат i-го
измерения. Наиболее вероятное значение
измеряемый
величины – ее среднеарифметическое
значение Величина
2
называется дисперсией результатов
измерений. При
большом числе измерений отношение ni
/N
характеризует
вероятность появления значений
измеряемой
величины в данном интервале с шагом
L.
Если ni
/N
разделить на величину шага интервала
L,
то значение величины
Рис.
1.3.
Кривые
распределения Гаусса для различных
значений
1=10,
2=20
и 3=30.
На
рис. 1.3. изображены кривые распределения,
соответствующие различным
. Из этого рисунка видно, что при малом
кривая уже, а максимум выше, что
соответствует более доброкачественным
измерениям. Распределение, соответствующее
предельной кривой, называют нормальным
(гауссовым) распределением. Оно
описывается функцией распределения где 2– как уже сказано выше, является дисперсией, - характеризует разброс измерений относительно среднеарифметического значения и называется стандартным отклонением или среднеквадратичной погрешностью. Функция
Гаусса является нормированной, т.е.
f(x)
удовлетворяет соотношению:
Интеграл имеет бесконечные пределы. Это означает, что измеряемая величина с вероятностью 1 (или 100%) лежит в пределах от - до + , или то, что нахождение измеряемой величины в этих пределах является событием достоверным. Функция плотности вероятности обладает следующими свойствами (см. рис. 1.2.): симметрична относительно х,. достигает максимального значения в точке х,. быстро стремится к нулю, когда |хi-х| становится большим по сравнению с .
|
6.Как рассчитывается точность нониуса? В науке и технике для определения длин и расстояний используется много приборов, обеспечивающих измерение их с различной точностью. Широко применяется для измерения длин масштабная линейка с нониусом. Нониусом называется дополнение к масштабу (линейному или круговому), позволяющее повысить точность измерения в 10, 20 раз. Линейный нониус - это маленькая линейка с делениями, которая может скользить вдоль масштабной линейки. Деления нониуса наносятся так, что (m-1) делению основного масштаба соответствует m делений нониуса (см. рис. 2.1.)
Рис. 2.1. Линейный нониус
Цена
деления основного масштаба известна,
пусть она равна а (обычно а=1 мм).
Обозначим цену деления нониуса х,
тогда
откуда,
Разница между ценой деления масштаба и нониуса называется точностью нониуса
Для измерения размера предмета совместим его начало с нулевым делением масштабной линейки, нониус приложим к концу предмета. Тогда длина предмета равна
где k – номер ближайшего деления основного масштаба, расположенного слева от «0» нониуса. Так как цена деления нониуса не равна цене деления масштаба, то обязательно найдется деление нониуса n, которое ближе всего совпадает с некоторым делением масштаба, тогда, как видно из рис. 2.2,
Следовательно,
т.е. длина отрезка, измеряемого с помощью нониуса, равна числу целых делений основного масштаба, умноженному на цену его деления, плюс номер деления нониуса, совпадающего с некоторым делением основного масштаба, умноженный на точность нониуса. Точность нониуса обычно указывается на измерительном приборе. Погрешность результатов измерений, проводимых с помощью нониуса, равна точности нониуса.
|
|
|
4. Какая надежность соответствуют стандартному отклонению? Вероятность того, что истинное значение находится внутри некоторого интервала от <x>-x до <x>+x, называется доверительной вероятностью (коэффициентом надежности, надежностью) а интервал - доверительным интервалом. При достаточно большом значении N доверительному интервалу <x>х соответствует =0,68, <x>2х соответствует =0,95, <x>3х соответствует =0,997. Мера приближения измеренного значения величены х к истинному значению х0 определяется физической сущностью измеряемой величины, а также физическими и конструктивными принципами, заложенными в методику измерений, поэтому бесконечное увеличение числа измерений не дает заметного увеличения точности. 1.2.6. Так как нет смысла стремиться к очень большому числу измерений, то при проведении эксперимента проводят ограниченное число опытов. Однако при этом для заданной надежности доверительный интервал, измеренный в долях , оказывается заниженным. Возникает вопрос, как изменяется надежность в зависимости от числа измерений? Зависимость эта сложна и не выражается в элементарных функциях. Множители, определяющие величину интервала в долях Sх в зависимости от и N, называются коэффициентами Стьюдента, обозначаются через t, и находятся из таблиц коэффициента Стьюдента. Доверительный
интервал х
можно рассчитать по формуле:
Конечный результат, в данном случае, представляется в виде: х = <x> x при =К%. (1.12) Очевидно, что при =0,68 t,1, но при N t,1. Доверительный интервал результата эксперимента обычно соответствует доверительной вероятности =0,95. При =0,95 t,2, но при N t,2.
|
7. Чему равно приборная погрешность микрометра, штангенциркуля? .Микрометр Для более точных измерений применяют микрометрические инструменты. Они бывают нескольких типов: микрометр для наружных измерений, микрометрический глубинометр и микрометрический нутромер. Микрометр для наружных измерений (рис. 2.4.) состоит из полого стержня, жестко соединенного скобой. В полость стержня ввинчен микрометрический винт (А). При измерении предмет зажимается между неподвижным стержнем и подвижным торцом микрометрического винта А. Микровинт вращают, держась за трещетку В. Вместе с микровинтом вращается барабан С, перемещаясь при этом поступательно относительно стержня. Отсчетное устройство микрометра состоит из двух шкал. Горизонтальная шкала стержня представляет собой двойную шкалу с ценой деления 0,5 мм, нанесенную по обе стороны продольной черты, таким образом, что верхняя сдвинута относительно нижней на половину деления. Цена деления шкалы барабана может быть установлена следующим образом. Пусть число делений круговой шкалы барабана n=50. Шаг микровинта h=0,5 мм, т.е. одному полному обороту микровинта (и барабана) соответвует линейное перемещение края барабана на 0,5 мм. Цена
деления круговой шкалы:
Штангенциркуль (рис.2.3.) состоит из миллиметрового масштаба М (шкалы прибора), жестко связанного с ножкой LA. Вдоль масштаба может перемещаться нониус N, с которым жестко связана вторая ножка LB и рейка F прибора. Подвижная часть штангенциркуля снабжена зажимным винтом С. Когда между ножками А и В отсутствует зазор, нулевые деления нониуса и шкалы совпадают. Для промера наружных размеров предмет вводят между ножками А и В, которые сдвигают до соприкосновения с предметом. Затем закрепляют подвижную ножку зажимом С и производят отсчет. Число целых миллиметров отсчитывается непосредственно по шкале прибора до нулевой метки нониуса, число долей миллиметра – по нониусу. При внутренних промерах употребляют ножки LL, для измерения глубины – рейку F. Штангенциркули изготовляют с нониусом n=10, 20, 50 делений. |
|
|
8. Приведите примеры прямых и косвенных измерений. Измерения как экспериментальные процессы весьма разнообразны. Это объясняется множеством экспериментальных величин, различным характером измерения величин, различными требованиями точности измерения и другие. Косвенное измерение — измерение, при котором искомое значение величины находится на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. -сопротивление резистора находим на основании закона Ома подстановкой значений силы тока и напряжения, получаемых в результате прямых измерений. (Проводим прямое измерение напряжения, проводим прямое измерение тока, потом на основании полученных ДВУХ чисел получаем косвенное "измерение" сопротивления) Прямые и косвенные измерения различают в зависимости от способа получения результата измерений. Прямое измерение – измерение, при котором искомое значение физической величины получают непосредственно. Как примеры прямых измерений приведены: измерение длины детали микрометром, силы тока амперметром, массы на весах. В ходе прямых измерений искомое значение величины определяют непосредственно по устройству отображения измерительной информации применяемого средства измерений. Формально без учета погрешности измерения они могут быть описаны выражением Q = х,где Q – измеряемая величина, х – результат измерения. Косвенное измерение – определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. Далее сказано, что вместо термина косвенное измерение часто применяют термин косвенный метод измерений. Этот вариант предпочтительно не использовать как явно неудачный. При косвенных измерениях искомое значение величины рассчитывают на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Формальная запись такого измерения Q = F (X, Y, Z,…),где X, Y, Z,… – результаты прямых измерений. Принципиальной особенностью косвенных измерений является необходимость обработки (преобразования) результатов вне прибора (на бумаге, с помощью калькулятора или компьютера), в противоположность прямым измерениям, при которых прибор выдает готовый результат. Классическими примерами косвенных измерений можно считать нахождение значения угла треугольника по измеренным длинам сторон, определение площади треугольника или другой геометрической фигуры и т.п. Один из наиболее часто встречающихся случаев применения косвенных измерений– определение плотности материала твердого тела. Например, плотность ρ тела цилиндрической формы определяют по результатам прямых измерений массы т, высоты h и диаметра цилиндра d, связанных с плотностью уравнением
|
11.Как найти среднюю квадратичную погрешность среднего арифметического? Пусть х(1), х(2), …, х(i), …, х(n)– результаты отдельных измерений, причем каждое из них характеризуется одной и той же дисперсией. Среднее арифметическое ряда измерений определяется по формуле:
Тогда дисперсия этой величины определяется как
Аналогично Средняя квадратичная погрешность среднего арифметического равна средней квадратичной погрешности отдельного результата, деленной на корень квадратный из числа измерений. Это фундаментальный закон возрастания точности при росте числа наблюдений.
|
|
|
9.Чему равна приборная погрешность стрелочного и цифрового измерительного прибора? Если погрешность прибора зависит от измеряемой величины, то она называется мультипликативной и предел допускаемой абсолютной погрешности выражается формулой хмакс приб = (а + вх), (2.6) где
в
– постоянная
величина, вх
– предельное значение мультипликативной
погрешности, а
– предельное значение аддитивной
погрешности. Таким образом,
мультипликативная погрешность прямо
пропорциональна значению измеряемой
величины х.
Источники мультипликативной
погрешности – действие влияющих
величин на параметры элементов и узлов
средств измерений. Зона погрешности
при наличии аддитивной и мультипликативной
составляющей показана на рисунке 2.1
б.
Инструментальная погрешность
электроизмерительных приборов
определяется их классом точности.
Класс
точности
(максимальная приведенная погрешность)
– это отношение максимальной абсолютной
погрешности прибора к пределу измерения
величины (полному значению шкалы).
Его, как и относительную погрешность,
выражают в процентах. Класс точности
показывает, сколько процентов
максимальная инструментальная
погрешность составляет от всей шкалы
прибора:
ГОСТом
установлено 8 классов точности
измерительных приборов: 0,05; 0,1; 0,2; 0,5;
1,0; 1,5; 2,5; 4,0. Зная класс точности прибора
и предельное значение измеряемой
величины, можно определить абсолютную
и относительную инструментальную
погрешность измерения:
Из формулы (2.9) видно, что чем ближе значение измеряемой величины к пределу измерения, тем меньше относительная инструментальная погрешность. У приборов, аддитивная составляющая погрешности которых преобладает надмультипликативной, класс точности выражается одним числом. К таким приборам относится большинство аналоговых стрелочных приборов. Относительная инструментальная погрешность в этом случае находится просто по формуле (2.9). Класс точности средств измерения, у которых аддитивная и мультипликативная составляющие основной погрешности соизмеримы, обозначается двумя числами, разделенными косой чертой: c/d. Причем класс точности должен удовлетворять условию c/d>l. К приборам, класс точности которых выражается дробью, относятся цифровые показывающие приборы. Их максимальная относительная погрешность определяется по формуле:
17.Нарисовать график функции Гаусса для двух различных значений стандартного отклонения, дать объяснение
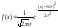
Кривые распределения Гаусса для различных значений σ: σ(1)=10, σ(2)=20 и σ(3)=30. <x>=500. На рис. изображены кривые распределения, соответствующие различным σ . Из этого рисунка видно, что при малом σ кривая уже, а максимум выше, что соответствует более доброкачественным измерениям. На практике чаще бывает необходимо определить погрешность среднегоарифметического. Площадь под кривой Гаусса всегда остается постоянной не смотря на изменение σ.
16.Записать условие нормировки функции Гаусса, объяснить его смысл Распределение
плотности вероятности по интер-валам:
1- при конечном числе измерений
(приведенная гистограмма); 2-кривая
Гаусса. Теория вероятности позволяет вычислить форму предельной гладкой кривой, к которой стремятся гистограммы при неограниченном увеличении числа опытов. Эта предельная кривая носит название кривой Гаусса. Распределение,
соответствующее предельной кривой,
называют нормальным (гауссовым)
распределением. Оно описывается
функцией распределения:
удовлетворяет соотношению:
- симметрична относительно <х>, -достигает максимального значения в точке <х>, - быстро стремится к нулю, когда |х(i)-<х>| становится большим по сравнению с σ .
20. Чему будет равна абсолютная погрешность измерения , если случайная погрешность равна нулю? Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Погрешность делится на 2 вида: на абсолютной и относительной погрешности. Абсолютная погрешность: Допустим, что истинное значение некоторой величины есть х0 . Измеряя эту величину, как правило, получают результат, отличный от х0 . Если измерение выполняется неоднократно, то результаты измерений не только отличаются от х0 , но в большинстве случаев различны и между собой. Обозначим результаты измерений х1, х2, х3, …, хп , Тогда разность хi =хi - х0, где i=1,2, …, п , (1.1) называется абсолютной погрешностью измерения. Она выражена в единицах измеряемой величины При классификации погрешностей по их свойствам различают погрешности систематические, случайные и промахи. Случайные
погрешности – погрешности, изменяющиеся
случайным образом. При этом различия
между результатами отдельных измерений
индивидуально непредсказуемы, а
закономерности проявляются лишь при
значительном числе измерений.
|
12.Как найти доверительный интервал? Вероятность того, что истинное значение находится внутри некоторого интервала от <x>-∆x до <x>+∆x, называется доверительной вероятностью (коэффициентом надежности, надежностью) а интервал - доверительным интервалом. При достаточно большом значении N доверительному интервалу <x>±σ<х> соответствует α=0,68, <x>±2σ<х>соответствует α=0,95, <x>±3σ<х> соответствует α=0,997. Мера σ приближения измеренного значения величеных к истинному значению х(0) определяется физической сущностью измеряемой величины, а также физическими и конструктивными принципами, заложенными в методику измерений, поэтому бесконечное увеличение числа измерений не дает заметного увеличения точности. Так как нет смысла стремиться к очень большому числу измерений, то при проведении эксперимента проводят ограниченное число опытов. Однако при этом для заданной надежности α доверительный интервал, измеренный в долях σ, оказывается заниженным. Зависимость (как изменяется надежность в зависимости от числа измерений) эта сложна и не выражается в элементарных функциях. Множители, определяющие величину интервала в долях S<х> в зависимости от α и N, называются коэффициентами Стьюдента, обозначаются через t(α,Ν) и находятся из таблиц коэффициента Стьюдента. Доверительный интервал ∆х можно рассчитать по формуле: Доверительный интервал результата эксперимента обычно соответствует доверительной вероятности α=0,95. При α=0,95 tα,Ν>2, но при N→∞ t(α,Ν)→2.
13.14.15.Как называется событие, вероятность которого равна 1? Что Вы можете сказать об этом событии? Случайными событиями называются такие события, которые могут произойти или не произойти при осуществлении совокупности условий, связанных с возможностью появления данных событий. Случайные события обозначают буквами A, B, C,... . Каждое осуществление рассматриваемой совокупности называется испытанием. Число испытаний может неограниченно возрастать. Отношения числа m наступлений данного случайного события A в данной серии испытаний к общему числу n испытаний этой серии называется частотой появления события A в данной серии испытаний (или просто частотой события А) и обозначается Р*(А). Таким образом, P*(A)=m/n. Частота случайного события всегда заключена между нулем и единицей: 0 ≤ P*(A) ≤ 1. Массовые случайные события обладают свойством устойчивости частоты: наблюдаемые в различных сериях однородных испытаний (с достаточно большим числом испытаний в каждой серии) значения частоты данного случайного события колеблются от серии к серии в довольно тесных пределах. Именно это обстоятельство позволяет при изучении случайных событий применять математические методы, приписывая каждому массовому случайному событию его вероятность, за которую принимается то (вообще говоря заранее неизвестное) число, около которого колеблется наблюдаемая частота события. Вероятность случайного события А обозначается через Р(А). Вероятность случайного события, как и его частота, заключена между нулем и единицей: 0 ≤ P(A) ≤ 1. Достоверному событию приписывают вероятность Р(А)=1. Невозможному событию приписывают вероятность Р(А)=0. Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю. Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1) — вероятности события A. Совмещением (или произведением) двух событий A иВ называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА. Аналогично, совмещением нескольких событий, например A, В иС, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С. Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В. Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С. Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное.
18.Как определяется погрешность косвенных измерений? В
частном случае вместо формулы
В
частном случае, если все показали
степени измеряемых величин равны 1,
формула
т.е. для таких функции относительная погрешность равна корню квадратному из суммы квадратов относительных погрешностей прямых измерений.
19. Как определяется результирующая погрешность измерений.
Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Погрешность делится на 2 вида: на обсолютной и относительной погрешности. Абсолютная погрешность: Допустим, что истинное значение некоторой величины есть х0 . Измеряя эту величину, как правило, получают результат, отличный от х0 . Если измерение выполняется неоднократно, то результаты измерений не только отличаются от х0 , но в большинстве случаев различны и между собой. Обозначим результаты измерений х1, х2, х3, …, хп , Тогда разность хi =хi - х0, где i=1,2, …, п , (1.1) называется абсолютной погрешностью измерения. Она выражена в единицах измеряемой величины. Относительная погрешность: Для оценки точности эксперимента рассчитывают относительную погрешность эксперимента. Относительная погрешность – это погрешность, выраженная в долях истинного значения измеренной величины:
Часто
ее выражают в процентах:
Результирующая погрешность является суммой двух составляющих: систематической погрешности и случайной погрешности Систематической погрешностью измерения называется составляющая погрешности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Например, шкала измерительной линейки неравномерна, капилляр термометра имеет в различных участках различный диаметр, весы неравноплечные, стрелка амперметра при отсутствии тока не стоит на нуле и прочие. Эти погрешности, как правило, можно учесть, а поэтому устранить введением поправки к измеренному значению (учесть деление, на котором стоит стрелка амперметра при отсутствии тока и каждый раз вычитать его из показаний прибора). Систематическую погрешность измерения экспериментально можно обнаружить либо сопоставлением данного результата с результатом измерения этой же величины, но полученным другим методом, либо путем использования более точных средств измерений. Однако обычно систематические погрешности оценивают путем теоретического анализа условий измерения, основываясь на известных свойствах средств измерений. Случайные погрешности – погрешности, изменяющиеся случайным образом. При этом различия между результатами отдельных измерений индивидуально непредсказуемы, а закономерности проявляются лишь при значительном числе измерений.
|
|
|
21) Как определяется цена деления измерительного прибора? Измерительный прибор, средство измерений, дающее возможность непосредственно отсчитывать значения измеряемой величины в установленном диапозоне. Наиболее распространены измерительные приборы прямого действия - измерительные преобразователи и измерительные приборы сравнения, в которых измеряемая величина сравнивается с соответствующей мерой (весы, компаратор, потенциометр). Измерительные приборы, как правило, имеют шкалу. Это значит, что на нем нанесены штриховые деления, а рядом написаны числовые значения величин, соответствующие делениям. Расстояния между двумя штрихами, возле которых написаны значения физической величины, могут быть дополнительно разделены еще на несколько делений, не подписанных числами. Расстояние между двумя ближайшими штрихами называется ценой деления шкалы прибора. тобы подсчитать цену делений шкалы, нужно: а) выбрать на шкале два ближайших оцифрованных штриха б) сосчитать количество делений между ними в) разность значений около выбранных штрихов разделить на количество делений
22) Вероятность события ,которого равна нулю называется невозможным событием. Событие которое не может произойти в результате эксперимениа.То есть событие, не содержащее ни одного элементарного исхода. Невозможному событию приписывают вероятность Р(А)=0. Вероятность – число, заранее неизвестное, около которого колеблется наблюдаемая частота события. Так как кроме невозможных различают еще и случайные и достоверные события рассмотрим их кратко: Вероятность случайного события А обозначается через Р(А). Вероятность случайного события, как и его частота, заключена между нулем и единицей: 0 ≤ P(A) ≤ 1. Достоверному событию приписывают вероятность Р(А)=1. Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю. Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1) — вероятности события A.
|
23Каким образом может влиять масса и форма подвеса маятника на его движение? Приведет ли учет наличия подвеса к увеличению или уменьшению периода колебаний? Физическим маятником называется твердое тело произвольной формы, укрепленное на неподвижной горизонтальной оси (не проходящей через его центр масс) и способное совершать колебания относительно этой оси. Математическим маятником называют идеализированную систему ,состоящую из евесомой и нерастяжимой нити,на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити Если
колеблющееся тело нельзя представить
как материальную точку, маятник
называется физическим. При отклонении
маятника от положения равновесия на
угол _ возникает вращательный момент
, стремящийся вернуть маятник в
положение равновесия. Этот момент
равен
Где m- масса маятника , а l – расстояние между точкой подвеса О и центром масс С маятника. Он имеет такое направление , что стремится вернуть маятник в положение равновесия, и аналогичен в этом отношении квазиупругой силе. Поэтому так же, как смещению и квазиупругой силе, моменту N и угловому смещению _ нужно приписывать противоположные знаки. Обозначив
момент инерции маятника относительно
оси, проходящей через точку подвеса,
буквой I
, можно написать:
Из этих уравнений следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром масс маятника.
|
|
|
24. Объясните почему кривая зависимости периода Т колебаний физического маятника от величины а , если ее представить на рисунке , симметрична относительно центра масс, хотя сам физический маятник такой симметрией может и не обладать. Зависимость периода колебаний физического маятника от расстояния между точкой подвеса и центром масс Подставив I= I0 + ma2 , (5.10) где
I0
- момент инерции тела относительно
оси, проходящей через центр масс., в
В
случае а
вторым слагаемым под корнем в выражении
(5.13) можно пренебречь по сравнению с
первым, тогда будем иметь:
Период колебаний физического маятника принимает минимальное значение на некотором расстоянии а* от точки подвеса до центра масс. Найти это расстояние а* и соответствующий ему период колебаний Тmin можно из условия экстремума:
|
Отсюда,
используя (5.13), получим следующие
выражения:
Приведенная длина l0 определяется графически с помощью экспериментально полученной зависимости периода колебаний физического маятника от расстояния между точкой подвеса и центром масс, качественно изображенной на рис.5.2. Как видно, эта кривая состоит из двух ветвей, симметрично расположенных относительно оси ординат (ось Т).
|
|
|
25.
Представить в виде графика зависимость
скорости и пути ,пройденного телом ,
при равномерном прямолинейном
движении?
26) Представить в виде графика зависимость ускорения,скорости и пути ,пройденного телом , при равноускоренном прямолинейно
|
27) Какие силы называются консервативными? Дайте примеры Если
частица в каждой точке пространства
подвержена воздействию других тел,
то говорят, что эта частица находится
в поле сил. Например: заряженная частица
е в электрическом поле, возбуждаемом
неподвижным зарядом q.
Это поле характерно тем, что направление
силы, действующей на частицу в любой
точке пространства проходит через
неподвижный центр (заряд q),
а величина силы зависит только от
расстояния до этого центра: F=F(r)=k
|
|
|
28) Какие силы не являются консервативными? Дайте примеры Если
частица в каждой точке пространства
подвержена воздействию других тел,
то говорят, что эта частица находится
в поле сил. Например: заряженная частица
е в электрическом поле, возбуждаемом
неподвижным зарядом q.
Это поле характерно тем, что направление
силы, действующей на частицу в любой
точке пространства проходит через
неподвижный центр (заряд q),
а величина силы зависит только от
расстояния до этого центра: F=F(r)=k
|
29) Как понимать термин « Физическая величина является функцией состояния»? првиедите примеры. Любая физическая величина, имеющая определенное значение для каждого равновесного состояния системы, является функцией состояния и называется термодинамической величиной. Например, у идеального газа к ним относятся давление, объём, температура и масса. Эти параметры являются зависимыми, они связаны уравнением состояния. Функции состояния зависят только от текущего состояния системы и не зависят от пути, по которому система пришла в это состояние. Функции состояния в термодинамике включают: температуру, давление, объём, энтропию, а также термодинамические потенциалы. В зависимости от выбранной модели некоторые из этих величин, строго говоря, могут быть не функциями, а независимыми переменными. Эти величины не являются независимыми. Связь между термодинамическими параметрами для конкретной системы называется уравнением состояния. В случае, если известно каноническое уравнение состояния, задание любой пары параметров из следующих: энтропия и объём, энтропия и давление, температура и объём, температура и давление, позволяет вычислить остальные два параметра
30)Как понимать « Физическая величина является функцией процесса»? првиедите примеры. Функции процесса зависят не только от текущего состояния системы, но также и от пути, по которому система пришла в данное состояние. Функции процесса в термодинамике включают: количество теплоты термодинамическую работу. Эти
величины, однако, могут быть «превращены»
в функции состояния с помощью
интегрирующего
множителя:
|
|
|
31.Какое движение называетсяьпоступательным? Запишите уравнение динамики для поступательного движения тела. Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени При поступательном движении все точки тела получают за один и тот же промежуток времени равные по величине и направлению перемещения, вследствие чего скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Поэтому достаточно определить движение одной из точек тела (например, его центра инерции) для того, чтобы охарактеризовать полностью движение всего тела. Любая прямая, проведенная между каким-либо точками тела, перемещается параллельно самой себе. Углы Эйлера при поступательном движении постоянны. Таким образом, это движение полностью характеризуется заданием движения какой-либо одной точки тела, т.е. поступательно движущееся тело имеет три степени свободы. В кинематическом отношении это движение полностью эквивалентно движению материальной точки. Уравнение динамики для поступательного движения тела: F=ma
p=mv= |
32.Какое движение называется вращательным? Запишите уравнение моментов для вращательного движения тела. Вращательное движение —это такое движение, при котором две точки тела остаются все время неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все точки твердого тела, лежащие на оси вращения, неподвижны. Другие точки твердого тела движутся по окружностям в плоскостях, перпендикулярных оси вращения. Центры этих окружностей лежат на оси вращения. Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени. Уравнение моментов для вращательного движения тела:
M-момент
силыя. I-момент
инерции.
|
|
|
33. Сформулируйте и запишите основной закон динамики вращательного движения.
При
вращении материальной точки массы тi
по окружности радиуса гi
момент ее импульса в проекции на ось
вращения равенLi=miiri
Линейная
скорость движения i
связана с угловой скоростью
соотношением
i=ri
, поэтому Li=miri2
. Если вокруг оси 0 вращается система
материальных точек с одной и той
же угловой скоростью ,
то основной закон динамики вращательного движения в проекции на ось вращения можно записать:
где М - проекция суммарного момента внешних сил на ось вращения. Уравнение вращения т.т. вокруг неподвижной оси:
. Произведение момента инерции твердого тела относительно неподвижной оси вращения на угловое ускорение равно моменту внешних сил относительно той же оси.
34. что понимают под моментом инерции тела относительно некоторой оси? При
вращении материальной точки массы тi
по окружности радиуса гi
момент ее импульса в проекции на ось
вращения равенLi=miiri
Линейная
скорость движения i
связана с угловой скоростью
соотношением
i=ri
, поэтому Li=miri2
. Если вокруг оси 0 вращается система
материальных точек с одной и той
же угловой скоростью ,
то основной закон динамики вращательного движения в проекции на ось вращения можно записать:
где М - проекция суммарного момента внешних сил на ось вращения. Уравнение вращения т.т. вокруг неподвижной оси:
Произведение момента инерции твердого тела относительно неподвижной оси вращения на угловое ускорение равно моменту внешних сил относительно той же оси.
|
35.36.От чего зависит момент инерции тела? От чего он не зависит? Момент
инерции тела – физическая величина,
аналогичная массе при поступательном
движении; она зависит от формы, размеров,
массы тела и ее распределения внутри
тела, а также от выбора оси вращения,
не зависит от скорости движения, и
характеризует инертность тела при
вращательном движении. Так же момент
инерции твердого тела есть величина
аддитивная. Момент инерции тела равна
моменту инерции частей этого тела : Тонкий стержень длины lJ= 1/12 ml^2 Сплошной цилиндр радиуса RJ= ½ mR^2 Тонкий диск радиуса RJ= ½ mR^2 Шар радиуса RJ=2/5 mR^2 Основное уравнение динамики вращательного движения абсолютно твердого тела вокруг неподвижной оси, называемая уравнением моментов в проекции на эту ось:
I
– момент инерции тела относительно
этой же оси;
Теорема
Штейнера:
момент инерции относительно произвольной
оси равен моменту инерции относительно
оси, параллельной данной и проходящей
через центр масс тела, плюс произведение
масс тела на квадрат расстояния между
осями:
37.Как найти момент инерции тела, которое в данных условиях нельзя считать материальной точкой?
Моментом
инерции механической
системы относительно
неподвижной оси («осевой момент
инерции») называется величина Ja,
равная сумме произведений масс
всех n материальных
точек системы на квадраты их
расстояний до оси:
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
|
|
|
38. Какая формула упрощает расчет момента инерции тела относительно оси, не проходящей через центр масс? т.Гюйгенса - Штейнера, момент инерции груза относительно оси вращения:
осью, проходящей через центр масс полого цилиндра параллельной оси вращения.
40. перечислите причины , дающие погрешность в эксперименте. Скажется ли на точности измерений в лабораторной работе №3 колебание груза при его падении, а также неуравновешенность диска?
Момент инерции от-но произвольной оси = сумме от-но, оси параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между ними Момент инерции тела – физическая величина, аналогичная массе при поступательном движении; она зависит от формы, размеров, массы тела и ее распределения внутри тела, а также от выбора оси вращения, и характеризует инертность тела при вращательном движении. Определение момента инерции диска методом колебаний В работе используется установка, на ободе которой укреплен массивный шар
Рис.3.2. Схема экспериментальной установки для определения момента инерции диска методом колебаний.
Пренебрегая моментом сил трения, можно написать уравнение движения диска с шаром в следующем виде:
где I- момент инерции диска c валом относительно оси вращения OO, I1 - момент инерции шара относительно оси вращения OO, вычисляемый по теореме Гюйгенса – Штейнера:
где R и R1 – радиусы диска и шара соответственно, m1 - масса шара, – угол отклонения диска от положения равновесия. При малых углах отклонения можно принять sin ≈ и уравнение (3.5) можно написать в виде:
Как известно, решением такого дифференциального уравнения будет периодическая функция
где α0- угловая амплитуда колебаний, - начальная фаза, ω0 - циклическая частота колебаний:
Измерив период колебаний диска с шаром Т0 и зная массу m1 и радиус шара R1, из формул (3.6) и (3.9) найдем момент инерции диска относительно оси вращения:
41.Как определить направление момента силы? Момент импульса частицы относительно точки называют вектор М, равный векторному произведению векторов rи p: М=[rp]. dM/dt=[dr/dt,p] + [r,dp/dt] [dr/dt,p]=0 Согласно второму закону Ньютона, dp/dt=F,гдеF – равнодействующая всех сил, приложенных к частице. Cледовательно: dM/dt=[rF] Обозначим левую часть N, запишем N=[rF] – момент силы. Момент силы – векторная величина, равная векторному произведению радиус вектора, характеризующий положение частицы относительно некоторой точки выбранной системы отсчета, на равнодействующую всех сил, приложенных к частице.Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика(«правилом правого винта»): если направление движения ручки буравчика (или штопора) совместить с направлением вращения, то направление движения всего буравчика совпадет с направлением вектора угловой скорости.
42.Как определить направление угловой скорости? Угловая
скорость —
векторная величина, характеризующая
скорость вращения тела. Вектор угловой
скорости по величине равен углу
поворота тела в единицу времени: Направлен по оси вращения согласно правилу буравчика(«правилом правого винта»): если направление движения ручки буравчика (или штопора) совместить с направлением вращения, то направление движения всего буравчика совпадет с направлением вектора угловой скорости. Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. 43.Как определить направление углового ускорения? Угловое ускорение - векторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.Угловое ускорение равно первой производной от угловой скорости по времени.Формула угловой скорости:
Вектор
углового ускорения α
направлен вдоль оси вращения (в сторону
44. При каком условии мы имеем право считать в лабораторной работе №4 «Изучение основного закона динамики вращательного движения» линейное ускорение точек на ободе шкива равным ускорению поступательного движения груза? Момент
сил создается грузом m, привязанным
к нити Н, которая навита на один
из шкивов. Если момент сил трения Mтр,
приложенный к оси маятника, мал по
сравнению с моментом силы натяжения
нити, то проверка уравнения
|
39. В методе колебаний для определения момента инерции диска в лабораторной работе №3 применяется теория малых колебаний. Какие упрощения при этом допускаются? Момент инерции тела – физическая величина, аналогичная массе при поступательном движении; она зависит от формы, размеров, массы тела и ее распределения внутри тела, а также от выбора оси вращения, и характеризует инертность тела при вращательном движении. Определение момента инерции диска методом колебаний В работе используется установка, на ободе которой укреплен массивный шар
Рис.3.2. Схема экспериментальной установки для определения момента инерции диска методом колебаний.
Пренебрегая моментом сил трения, можно написать уравнение движения диска с шаром в следующем виде:
где I- момент инерции диска c валом относительно оси вращения OO, I1 - момент инерции шара относительно оси вращения OO, вычисляемый по теореме Гюйгенса – Штейнера:
где R и R1 – радиусы диска и шара соответственно, m1 - масса шара, – угол отклонения диска от положения равновесия. При малых углах отклонения можно принять sin ≈ и уравнение (3.5) можно написать в виде:
Как известно, решением такого дифференциального уравнения будет периодическая функция
где α0- угловая амплитуда колебаний, - начальная фаза, ω0 - циклическая частота колебаний:
Измерив период колебаний диска с шаром Т0 и зная массу m1 и радиус шара R1, из формул (3.6) и (3.9) найдем момент инерции диска относительно оси вращения:
45. Можно ли определить момент инерции маятника Обербека, используя закон сохранения механической энергии? Если
Т - сила натяжения нити,
Силу натяжения нити можно найти из уравнения движения груза:
тогда Момент
сил трения Мтр
обычно оказывается довольно велик
и зависит от скорости вращения, Мтр
способен существенно исказить
результаты опыта, однако, в первом
приближении можно принять момент
сопротивления постоянным и не зависящим
от скорости, тогда с учетом момента
силы трения уравнение можно записать
в виде: М-Mтр
46.Дайте определение физического маятника Физическим маятником называется твердое тело произвольной формы, укрепленное на неподвижной горизонтальной оси (не проходящей через его центр масс) и способное совершать колебания относительно этой оси.
В состоянии устойчивого равновесия физического маятника линия, проходящая через точки подвеса «О» и центра масс «С», направлена вертикально. Если маятник отклонить от положения равновесия на некоторый угол α и отпустить, то он будет совершать колебательное движение под действием момента силы тяжести относительно оси вращения. Проекция на ось вращения момента силы тяжести равна:
где m – масса маятника, g – ускорение свободного падения, a – расстояние от точки подвеса «О» до центра масс «С». Уравнение движения (уравнение моментов) физического маятника в проекции на ось вращения имеет следующий вид:
где I – момент инерции маятника относительно оси вращения. Время Т одного полного колебания, называемое
периодом колебаний, определяется
выражением: Приведенная длина физического маятника равна длине математического маятника с периодом колебаний, равным
периоду колебания для данного
физического маятника. Точка, которая лежит на прямой, проходящей че-рез точку подвеса и центр масс, и находится на расстоянии приведенной длины от точки подвеса, называется центром качания.
|
|
|
47. Дайте определение математического маятника. Математическим
маятником
называют тело небольших размеров,
подвешенное на тонкой нерастяжимой
нити, масса которой пренебрежимо мала
по сравнению с массой тела. В положении
равновесия, когда маятник висит по
отвесу, сила тяжести
Собственная
частота малых колебаний математического
маятника:
T
= 2π/ 48.Какие колебания называются гармоническими? По какому закону изменяется смещение при гармоническом колебании? Механическими колебаниями называются периодические изменения физической величины за равные промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f (t). Примерами простых колебательных систем могут служить груз на пружине или математический маятник. Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением: x(t)
= Asin(ωt
+ φ) илиx(t)
= Acos(ωt
+ φ),где х —
значение изменяющейся величины, t —
время, остальные параметры - постоянные:
А —
амплитуда колебаний, ω —
циклическая частота колебаний, (ωt
+ φ) — полная фаза колебаний,
Время Т одного полного колебания, назыв. периодом колебаний.Физическая величина, обратная периоду колебаний, называется частотой колебаний: ν = 1/Т. ω(0)=2πν=2π/Т – циклическая частота. 49.Каков физический смысл термина «приведённая длина физического маятника»? Выясним физический смысл термина «приведенная длина физического маятника». Время
Т одного полного колебания, называемое
периодом колебаний, определяется
выражением:
Приведенная
длина физического маятника равна
длине математического маятника с
периодом колебаний, равным периоду
колебания для данного физического
маятника:
50. Как выглядят кривые зависимости периода колебаний от расстояния между точкой подвеса и центром масс для математического и физического маятников, изображённые на одном и том же графике? Зависимость периода колебаний физического маятника от расстояния между точкой подвеса и центром масс Подставив
I=
I0
+
ma2
, где
I0
- момент инерции тела относительно
оси, проходящей через центр масс., в
При а0 (точка подвеса приближается к центру масс) период колебаний Т стремится к бесконечности, что соответствует безразличному равновесию. С удалением точки подвеса от центра масс период колебаний Т маятника сначала уменьшается, а затем снова возрастает и с дальнейшим увеличением а опять стремится к бесконечности. В случае а вторым слагаемым под корнем можно пренебречь по сравнению с первым, тогда будем иметь:
Последняя формула соответствует периоду колебаний математического маятника. Действительно, пределу а соответствует пренебрежение размерами самого маятника по сравнению с расстоянием а от точки подвеса до центра масс - это и есть определение математического маятника Период колебаний физического маятника принимает минимальное значение на некотором расстоянии а* от точки подвеса до центра масс. Найти это расстояние а* и соответствующий ему период колебаний Тmin можно из условия экстремума:
Отсюда получим следующие выражения:
Приведенная длина l0 определяется графически с помощью экспериментально полученной зависимости периода колебаний физического маятника от расстояния между точкой подвеса и центром масс, качественно изображенной на рис. Как видно, эта кривая состоит из двух ветвей, симметрично расположенных относительно оси ординат (ось Т). 58. какие виды механического равновесия вы знаете? Статика
изучает условия равновесия тел. Во
многих задачах статики можно использовать
модель абсолютно твердого тела, т.е.
тела, размеры и форма которого считаются
неизменными. В инерциальной системе
отсчета твердое тело находится в
равновесии если векторная сумма всех
действующих на тело внешних сил и
векторная сумма моментов этих сил
равны нулю. Равновесие бывает устойчивым,
неустойчивым и безразличным. Равновесие
устойчиво, если при малых смещениях
действующие силы стремятся вернуть
тело в положение равновесия, и
неустойчиво, если силы уводят его
дальше от равновесия. При безразличном
равновесии соседние положения также
являются равновесными. Устойчивому
равновесию соответствует минимум
потенциальной энергии тела по отношению
к ее значениям в соседних положениях,
неустойчивому – максимум.
|
51.Запишите и сформулируйте второй закон Ньютона. Второй закон Ньютона: сила есть производная импульса материальной точки по времени :F=dP/dt - (уравнение движения материальной точки). F=dP/dt=|P=mU|=m*dU/dt=ma. Единицей силы в СИ является ньютон. 1 ньютон – сила, которая сообщается телу массой 1 кг ускорением 1 м/с^2. Если на тело одновременно действуют несколько сил (например, F(1), F(2) и F(3)) то под силой Fв формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил:
Если равнодействующая сила F=0 то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения 52.Какую роль играет масса в поступательном движении? Опыт показывает, что всякое тело «оказывает сопротивление» при любых попытках изменить его скорость – как по модулю. Так и по направлению. Это свойство, выражающее степень неподатливости тела к изменению его скорости, называют инертностью. У различных тел оно проявляется в разной степени. Мерой инертности служит величина, называемой массой. Тело с большей массой является более инертным, и наоборот. Единица массы в Си является килограмм. Масса обладает двумя свойствами: 1.масса – величина аддитивная, т.е. масса составного тела равна сумме масс его частей. 2.Масса тела как такового – величина постоянная, не изменяется при движений. 53.54.Какие колебания называются гармоническими? Механическими колебаниями называются периодические изменения физической величины за равные промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f (t). Примерами простых колебательных систем могут служить груз на пружине или математический маятник. Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением: x(t)
= Asin(ωt
+ φ) илиx(t)
= Acos(ωt
+ φ),где х —
значение изменяющейся величины, t —
время, остальные параметры - постоянные:
А —
амплитуда колебаний, ω —
циклическая частота колебаний, (ωt
+ φ) — полная фаза колебаний,
Время Т одного полного колебания, назыв. периодом колебаний. Физическая величина, обратная периоду колебаний, называется частотой колебаний: ν = 1/Т. ω(0)=2πν=2π/Т – циклическая частота. Первая
производная от перемешения x(t)
= Asin(ωt
+ φ) является скорость U=ωAcos(ωt
+ φ), а вторая производная – это есть
ускорение a=-
55. что называется периодом колебаний? Как он связан с частотой? Колебаниями называются те процессы, которые в той или иной степени повторяются с течением времени. Таким свойством обладают, например, качания маятника часов, колебания струны или ножек камертона и т.д. в зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические. В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные, автоколебания и параметрические колебания. Свободные- происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок. Вынужденные – в процессе этих колебаний подвергается воздействию внешней периодически изменяющейся силы. Автоколебания – как и вынужденные колебания, сопровождаются воздействием внешних сил, которые управляются самой системой. Кинематически,
т.е. по характеру зависимости от времени
некоторой физической величины x(t),
различают непериодические и
периодические колебания. При
периодических колебаниях любое
значение x(t)
повторяется через одинаковые промежутки
времени Т. Эти промежутки называются
периодом колебаний: x(t)=
x(t+Т)
=> [wₒ(t+T)+α]=[wₒt+α]+2π
=> T=2π/wₒ При
малых колебаниях математического
маятника, можно положить что sin
φ=φ. (Математический маятник это
идеализированная система, состоящая
из невесомой и нерастяжимой нити, на
корой подвешена масса сосредоточенная
в одной точке). Введя, кроме того,
обозначение g/l=wₒ².
из чего следует, что частота колебаний
математического маятника зависит
только от длины и ускорения силы
тяжести. Учитывая это, получаем: T=2π
Величина
обратная периоду Т и равная числу
колебаний в единицу времени называется
частотой колебаний: ν=1/Т.
За единицу частоты принимается частота
такого колебания, период т которого
равен 1 сек. Эту единицу называют Герцем
(Гц). Также следует, что: ν=wₒ/
2π. В математическом маятнике: T=(1/2π
) Наиболее важная разновидность периодических колебаний синусоидальные (или гармонические) колебания. Они описываются функцией вида: x(t)=Acosφ(t)=Acos(wt+φₒ). Где А-амплитуда колебания, (wt+φₒ) – фаза колебания, φₒ - значение фазы колебания в момент времени t=о – начальная фаза колебания.
56. что называется частотой колебаний? Как она связана с периодом? Колебаниями называются те процессы, которые в той или иной степени повторяются с течением времени. Таким свойством обладают, например, качания маятника часов, колебания струны или ножек камертона и т.д. в зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические. В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные, автоколебания и параметрические колебания. Свободные- происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок. Вынужденные – в процессе этих колебаний подвергается воздействию внешней периодически изменяющейся силы. Автоколебания – как и вынужденные колебания, сопровождаются воздействием внешних сил, которые управляются самой системой. Кинематически, т.е. по характеру зависимости от времени некоторой физической величины x(t), различают непериодические и периодические колебания. При периодических колебаниях за единицу времени совершается одинаковое количество колебаний, что называется частотой колебаний: ν=wₒ/ 2π. За единицу частоты принимается частота такого колебания, период которого равен 1 сек. Эту единицу называют Герцем (Гц). При
малых колебаниях математического
маятника, можно положить что sin
φ=φ. (Математический маятник это
идеализированная система, состоящая
из невесомой и нерастяжимой нити, на
корой подвешена масса сосредоточенная
в одной точке). Введя, кроме того,
обозначение g/l=wₒ².
из чего следует, что частота колебаний
математического маятника зависит
только от длины и ускорения силы
тяжести. Учитывая это, получаем: ν=(1/2π
) Период - величина, обратная частоте. Это одинаковые промежутки, через которые повторяется любое значение x(t). Измеряется в секндах. Период Т равен: Т =1/ ν а также: x(t)= x(t+Т) => [wₒ(t+T)+α]=[wₒt+α]+2π => T=2π/wₒ
Период
математического маятника: T=2π
Наиболее важная разновидность периодических колебаний синусоидальные (или гармонические) колебания. Они описываются функцией вида x(t)=Acosφ(t)=Acos(wt+φₒ) Где А-амплитуда колебания, (wt+φₒ) – фаза колебания, φₒ - значение фазы колебания в момент времени t=о – начальная фаза колебания.
57. что такое амплитуда колебаний. Колебаниями называются те процессы, которые в той или иной степени повторяются с течением времени. Таким свойством обладают, например, качания маятника часов, колебания струны или ножек камертона и т.д. в зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические. В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные, автоколебания и параметрические колебания. Свободные- происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок. Вынужденные – в процессе этих колебаний подвергается воздействию внешней периодически изменяющейся силы. Автоколебания – как и вынужденные колебания, сопровождаются воздействием внешних сил, которые управляются самой системой. Кинематически, т.е. по характеру зависимости от времени некоторой физической величины x(t), различают непериодические и периодические колебания. При периодических колебаниях любое значение x(t) повторяется через одинаковые промежутки времени Т. Эти промежутки называются периодом колебаний: x(t)= x(t+Т) => [wₒ(t+T)+α]=[wₒt+α]+2π => T=2π/wₒ
Величина обратная периоду Т и равная числу колебаний в единицу времени называется частотой колебаний: ν=1/ Т. За единицу частоты принимается частота такого колебания, период которого равен 1 сек. Эту единицу называют Герцем (Гц). ν=wₒ/ 2π. Наиболее важная разновидность периодических колебаний синусоидальные (или гармонические) колебания. Они описываются функцией вида x(t)=Acosφ(t)=Acos(wt+φₒ) Где А-амплитуда колебания, (wt+φₒ) – фаза колебания, φₒ - значение фазы колебания в момент времени t=о – начальная фаза колебания. Смещение х изменяется со временем по закону косинуса. По графику функции x(t)=Acosφ(t)=Acos(wt+φₒ) по горизонтали время tпо вертикали смещение х. Т.к. косинус изменяется в пределах от -1 до 1, значения х лежат в пределах от –А до +А. Амплитудой колебания называется величина наибольшего отклонения системы от положения равновесия. А-постоянная положительная величина. Ее значение определяется величиной первоначального отклонения или толчка, которым система была выведена из состояния равновесия.
|
60. Остается ли момент инерции физического маятника одинаковым относительно осей, проходящих через разные точки подвеса? Почему?
Физическим маятником называется твердое тело произвольной формы, укрепленное на неподвижной горизонтальной оси (не проходящей через его центр масс) и способное совершать колебания относительно этой оси.
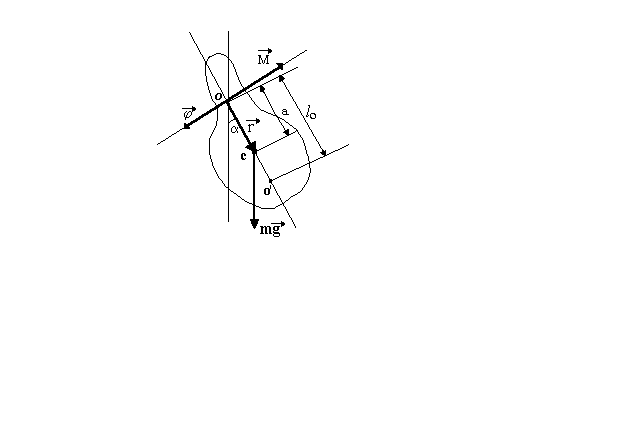
Уравнение моментов в проекции на ось вращения в данном случае имеет следующий вид:
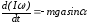 ,
(12.1)
,
(12.1)
где I - момент инерции маятника относительно оси вращения,
-
угол отклонения маятника от положения
равновесия,
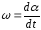 - угловая скорость,
- угловая скорость,
а - расстояние от оси вращения до центра тяжести маятника.
Если угол отклонения мал, то с достаточно большой точностью выполняется равенство:
sin = .. (12.2)
Кроме того, для данной оси вращения I=const, поэтому уравнение (12.1) можно переписать в виде:
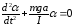 .
(12.3)
.
(12.3)
Введем обозначение:
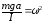 ,
(12.4)
,
(12.4)
тогда уравнение (12.3) примет вид:
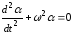 .
(12.5)
.
(12.5)
Уравнение такого типа является уравнением гармонических колебаний, а его решение имеет следующий вид:
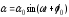 ,
(12.6)
,
(12.6)
где 0 - амплитуда колебания,
 -
циклическая частота,
-
циклическая частота,
Т - период колебаний,
0 - начальная фаза колебания.
Точка, которая лежит на прямой, проходящей через точку подвеса и центр масс, и находится на расстоянии приведенной длины от точки подвеса, называется центром качания.
По теореме Гюйгенса - Штейнера (см. Приложение) момент инерции твердого тела относительно произвольной оси равен:
I=I0 + ma2,
где I0 - момент инерции тела относительно оси, проходящей через центр масс.
Подставив в это равенство выражение (12.8) и разрешив его относительно l0, получим:
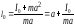 .
.
Из
этой формулы видно, что приведенная
длина равна сумме расстояния от точки
подвеса до центра масс (а) плюс некоторая
добавка
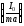 ,
то есть центр качания лежит ниже центра
масс (рис.12.1).
,
то есть центр качания лежит ниже центра
масс (рис.12.1).
Основное свойство центра качания физического маятника состоит в том, что при подвесе маятника на ось, проходящую через этот центр, период колебаний не изменится. Таким образом, при переносе точки подвеса в центр качания прежняя точка становится центром качания, то есть точка подвеса и центр качания обратимы.
61
62
63Запишите и объясните физический смысл уравнения неразрывности
В движущейся жидкости возьмем произвольный замкнутый контур С и через точки его в один и тот же момент времени проведем линии тока Совокупность линий тока, проведенных через все точки контура С, образуют трубчатую поверхность, называемую трубкой тока.
Масса жидкости, протекающая за время dt через поперечное сечение трубки, определяется выражением:
dm=uSdt , (6.1)
где –плотность жидкости;
u –скорость жидкости;
S – площадь нормального сечения трубки тока.
В случае стационарного течения масса жидкости, протекающая в единицу времени через любые сечения данной трубки тока, будет одной и той же.
Если взять два сечения трубки, площади которых равны S1 и S2, то можно написать:
1u1S1=2u2S2 . (6.2)
Эта формула выражает один из основных законов гидродинамики – закон сохранения массы или уравнения неразрывности.
Рассмотрим стационарное течение идеальной несжимаемой жидкости в трубке тока в поле силы тяжести. Применим к этому течению закон сохранения энергии. При этом пренебрегаем теплообменом, который может происходить между потоком жидкости и окружающей средой.
Выделим в жидкости бесконечно узкую трубку тока и рассмотрим часть жидкости, занимающую объем MNDC

Полная работа, совершаемая силами давления при перемещении выделенного объема жидкости в трубке тока из положения MNDC в положение M1N1D1C1 будет равна:
A=A1+A2= р1S1u1t - р2S2u2t . (6.7)
По закону сохранения энергии эта работа должна быть равна приращению полной энергии E выделенной части жидкости за время перемещения:
A=E (6.8)
Так как мы рассматриваем стационарное движение жидкости, энергия жидкости в объеме не изменится. Поэтому значение E равно разности энергии массы жидкости в объемах CDD1C1 и MN N1M1, которые соответствуют массе жидкости, вытекающей из сечения CD за времяt:
m2=u2S2 t
и втекающей через сечение MN за то же время t:
m1=u1S1t .
Полная
энергия единицы массы жидкости состоит
из суммы ее кинетической энергии
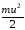 и потенциальной энергии в поле силы
тяжести mgh. Следовательно, приращение
полной энергии выделенного объема
жидкости равно:
и потенциальной энергии в поле силы
тяжести mgh. Следовательно, приращение
полной энергии выделенного объема
жидкости равно:
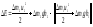 ,
(6.9)
,
(6.9)
здесь
h1
и h2
- высоты центров масс тел
 и
и
 с определенного начального уровня
(рис.6.2.).
с определенного начального уровня
(рис.6.2.).
На основании закона сохранения массы должно быть:
m1=m2=m ,
u1S1t=u2S2 t=uS t (6.10)
Подставляя значения A и E из (6.7) и (6.9) в (6.8), получим:
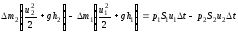 (6.11)
(6.11)
С учетом выражения (6.10), сокращая на m и перенося члены с одинаковыми индексами в одну сторону равенства, окончательно имеем:
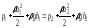 .
(6.12)
.
(6.12)
Эта формула впервые была получена петербургским академиком Д. Бернулли в 1738 году и называется уравнением Бернулли.
Формула (6.12) получена нами для двух произвольных сечений трубки тока. Это возможно тогда, когда сумма трех величин, входящих в уравнение Бернулли, остается постоянной по всей длине трубки тока. Следовательно, для любого сечения трубки тока при стационарном течении идеальной жидкости
 .
(6.13)
.
(6.13)
Первый
член р – называется статическим
давлением, второй член
 называется
динамическим давлением или динамическим
напором, третий член gh
называется нивелирным давлением.
называется
динамическим давлением или динамическим
напором, третий член gh
называется нивелирным давлением.
64. P+ρu2/2+ρgh=const
P-стат. давление
ρu2/2-динамический напор
ρgh-нивелирное давление
при движении жидкости по гори-зонтальной трубке сумма статического и динамического давлений сохраняет постоянное значение по длине трубки тока. При движении идеальной жидкости трубку тока можно заменить трубкой из твердого материала. Следовательно, для идеальной жидкости, движущейся в трубке переменного сечения, уравнение Бернулли также справедливо. Однако, при движении реальной (вязкой) жидкости в трубке появляются силы вязкого трения, действующие состороны стенок трубы на поток жидкости. Поэтому при
движении вязкой жидкости полное давление по длине трубы будет уменьшаться. Только для маловязких жидкостей (вода, бензин и др.) и на небольших участках длины трубопровода можно приближенно считать справедливым уравнение Бернулли.
65. Манометр, перемещающийся вместе с жидкостью, не будет изменять движения окружающих его слоев жидкости и покажет давление, которое было в потоке до его погружения. В этом случае жидкость неподвижна по отношению к манометру и измерение давления происходит так же, как и в гидростатике. На манометр, движущийся вместе с жидкостью, действует со стороны жидкости давление, которое соответствует степени сжатия жидкости в ненарушенном потоке. Давление, которое можно было бы измерить манометром, движущимся вместе с жидкостью, называют статическим давлением. Показание же неподвижного манометра, мембрана которого поставлена перпендикулярно к потоку, называют полным давлением. Итак, для измерения статического давления следует применять движущийся манометр, а для измерения полного давления — неподвижный. Однако на практике было бы крайне затруднительно применять движущийся манометр. Чтобы обойти это затруднение, прибору дают такую форму, при которой скорость течения вблизи места, где измеряется давление, не изменяется. Такой прибор можно сделать в виде узкой трубки с закругленным закрытым концом и с отверстиями сбоку (рис. 306, а). Струи потока, проходя мимо отверстий, практически сохраняют свою скорость неизменной, и в колене манометра, соединенного с такой трубкой, создается статическое давление. Такая трубка носит название зонда.

65. Статическое давление представляет собой давление газа, находящегося в трубопроводе. Оно характеризует потенциальную энергию потока и действует с одинаковой силой во все стороны.
Статические давления в поперечных сечениях трубки переменного сечения определяются по высоте столба жидкости в манометрических трубках (4), отсчитываемых от оси трубки переменного сечения (2):
рi=gh i,
где индекс i = 1, 2, 3 соответствует номерам поперечных сечений, =1000 кг/м3 – плотность воды,
g=9.804 м/с2 – ускорение свободного падения. Если значение hi подставим в метрах, то давление получим в Паскалях.
Манометр, перемещающийся вместе с жидкостью, не будет изменять движения окружающих его слоев жидкости и покажет давление, которое было в потоке до его погружения. В этом случае жидкость неподвижна по отношению к манометру и измерение давления происходит так же, как и в гидростатике. На манометр, движущийся вместе с жидкостью, действует со стороны жидкости давление, которое соответствует степени сжатия жидкости в ненарушенном потоке. Давление, которое можно было бы измерить манометром, движущимся вместе с жидкостью, называют статическим давлением. Показание же неподвижного манометра, мембрана которого поставлена перпендикулярно к потоку, называют полным давлением. Итак, для измерения статического давления следует применять движущийся манометр, а для измерения полного давления — неподвижный. Однако на практике было бы крайне затруднительно применять движущийся манометр. Чтобы обойти это затруднение, прибору дают такую форму, при которой скорость течения вблизи места, где измеряется давление, не изменяется. Такой прибор можно сделать в виде узкой трубки с закругленным закрытым концом и с отверстиями сбоку (рис. 306, а). Струи потока, проходя мимо отверстий, практически сохраняют свою скорость неизменной, и в колене манометра, соединенного с такой трубкой, создается статическое давление. Такая трубка носит название зонда.

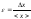 Часто ее выражают в процентах:
Часто ее выражают в процентах:
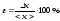
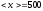 .
.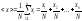 .
(1.7)
Тогда
дисперсия этой величины определяется
как
.
(1.7)
Тогда
дисперсия этой величины определяется
как (1.8)
таким
образом,
(1.8)
таким
образом,
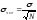 .
(1.9)
.
(1.9) (1.10)Средняя
квадратичная погрешность среднего
арифметического равна средней
квадратичной погрешности отдельного
результата, деленной на корень
квадратный из числа измерений. Это
фундаментальный закон возрастания
точности при росте числа наблюдений.
(1.10)Средняя
квадратичная погрешность среднего
арифметического равна средней
квадратичной погрешности отдельного
результата, деленной на корень
квадратный из числа измерений. Это
фундаментальный закон возрастания
точности при росте числа наблюдений.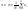 (1.2)
Величина
<х> стремится к истинному значению
х0
измеряемой величины при N.
Средней квадратичной погрешностью
отдельного результата измерения
называется величина
(1.2)
Величина
<х> стремится к истинному значению
х0
измеряемой величины при N.
Средней квадратичной погрешностью
отдельного результата измерения
называется величина
 . При
N
SN
стремится
к постоянному пределу :
. При
N
SN
стремится
к постоянному пределу :
 .
(1.4)
.
(1.4) будет
характеризовать относительное число
благоприятных случаев в единичном
интервале. Диаграмма, построенная для
yi,
показывает
распределение плотности вероятности
по интервалам и называется приведенной
гистограммой
будет
характеризовать относительное число
благоприятных случаев в единичном
интервале. Диаграмма, построенная для
yi,
показывает
распределение плотности вероятности
по интервалам и называется приведенной
гистограммой .
. , (1.5)
, (1.5)
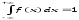 .
.
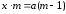
 .
.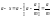 .
(2.7)
.
(2.7)
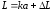 (см.
рис. 2.2.)
(см.
рис. 2.2.) .
. (2.8)
(2.8)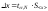 (1.11)
(1.11)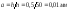

 .Если
случайная погрешность равна нулю, то
абсолютная погрешность равна приборной
погрешности. Если
же одна из погрешностей окажется три
и более раз меньше, то ее не учитывают.
.Если
случайная погрешность равна нулю, то
абсолютная погрешность равна приборной
погрешности. Если
же одна из погрешностей окажется три
и более раз меньше, то ее не учитывают.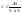 .
.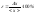 (1.!3)
(1.!3)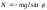
 В случае малых колебаний переходит в
известное нам уравнение:
В случае малых колебаний переходит в
известное нам уравнение:
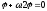 Через
w.2
обозначена в данном случае следующая
величина:
Через
w.2
обозначена в данном случае следующая
величина:
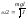
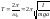 . получим
зависимость периода Т колебаний
физического маятника от расстояния
а между точкой подвеса «О» и центром
масс «С»:
. получим
зависимость периода Т колебаний
физического маятника от расстояния
а между точкой подвеса «О» и центром
масс «С»:
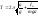 (5.13) На рис. 5.2. качественно изображена
зависимость (5.13). При а0
(точка подвеса приближается к центру
масс) период колебаний Т стремится к
бесконечности, что соответствует
безразличному равновесию. С удалением
точки подвеса от центра масс период
колебаний Т маятника сначала уменьшается,
а затем снова возрастает и с дальнейшим
увеличением а опять стремится к
бесконечности.
(5.13) На рис. 5.2. качественно изображена
зависимость (5.13). При а0
(точка подвеса приближается к центру
масс) период колебаний Т стремится к
бесконечности, что соответствует
безразличному равновесию. С удалением
точки подвеса от центра масс период
колебаний Т маятника сначала уменьшается,
а затем снова возрастает и с дальнейшим
увеличением а опять стремится к
бесконечности. Последняя
формула соответствует периоду колебаний
математического маятника. Действительно,
пределу а
соответствует пренебрежение размерами
самого маятника по сравнению с
расстоянием а от точки подвеса до
центра масс - это и есть определение
математического маятника
Последняя
формула соответствует периоду колебаний
математического маятника. Действительно,
пределу а
соответствует пренебрежение размерами
самого маятника по сравнению с
расстоянием а от точки подвеса до
центра масс - это и есть определение
математического маятника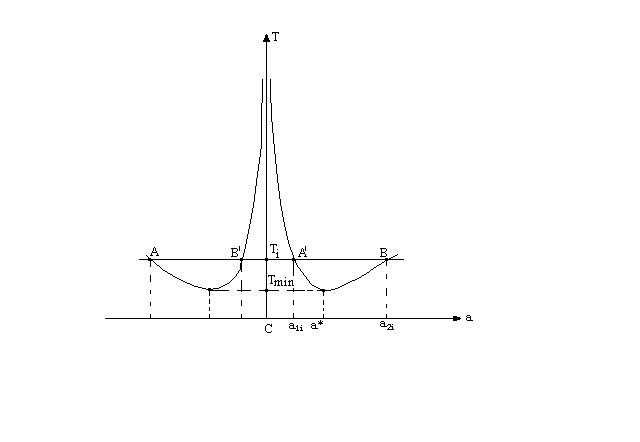
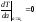 .
.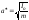
 (5.14)
(5.14)

 /
/ .
Поле сил, обладающее такими свойствами,
называется центральным. Если во всех
точках поля силы, действующие на
частицу, одинаковы по величине и
направлению (F=const),
поле называется однородным. Поле,
изменяющееся со временем, называется
нестационарным. Поле, остающееся
постоянным во времени, называют
стационарным. Для стационарного поля
может оказаться, что работа, совершаемая
над частицей силами поля, зависит лишь
от начального и конечного положения
частицы и не зависит от пути, по которому
двигалась частица. Силы, обладающие
таким свойством, называются
консервативными. Из независимости
работы консервативных сил от пути
вытекает, что работа таких сил на
замкнутом пути равна нулю. Например:
Сила тяжести является консервативной,
т.к. в любой точке имеет одинаковую
величину и одинаковое направление –
вниз по вертикали. Поэтому, независимо
от того, по какому из путей движется
частица, работа А определяется
выражением А=mg(
.
Поле сил, обладающее такими свойствами,
называется центральным. Если во всех
точках поля силы, действующие на
частицу, одинаковы по величине и
направлению (F=const),
поле называется однородным. Поле,
изменяющееся со временем, называется
нестационарным. Поле, остающееся
постоянным во времени, называют
стационарным. Для стационарного поля
может оказаться, что работа, совершаемая
над частицей силами поля, зависит лишь
от начального и конечного положения
частицы и не зависит от пути, по которому
двигалась частица. Силы, обладающие
таким свойством, называются
консервативными. Из независимости
работы консервативных сил от пути
вытекает, что работа таких сил на
замкнутом пути равна нулю. Например:
Сила тяжести является консервативной,
т.к. в любой точке имеет одинаковую
величину и одинаковое направление –
вниз по вертикали. Поэтому, независимо
от того, по какому из путей движется
частица, работа А определяется
выражением А=mg( .
Последнее выражение очевидно не
зависит от пути, отсюда следует что
сила тяжести консервативна. Такой же
результат получается для всякого
стационарного однородного поля.
Консервативными также являются: Сила
упругости, Сила всемирного тяготения
и т.д. Поле консервативных сил является
частным случаем потенциального
силового поля. Поле сил называется
потенциальным, если его можно описать
с помощью функции П (x,y,z,t),
градиент которой определяет силу в
каждой точке поля: F= ∇П.
функция П называется потенциальной
функцией или потенциалом. В случае
когда потенциал не зависит от времени,
т.е. П=П(x,y,z),
потенциальное поле оказывается
стационарным, а его силы – консервативными.
В этом случае П(x,y,z)=
-U(x,y,z).
.
Последнее выражение очевидно не
зависит от пути, отсюда следует что
сила тяжести консервативна. Такой же
результат получается для всякого
стационарного однородного поля.
Консервативными также являются: Сила
упругости, Сила всемирного тяготения
и т.д. Поле консервативных сил является
частным случаем потенциального
силового поля. Поле сил называется
потенциальным, если его можно описать
с помощью функции П (x,y,z,t),
градиент которой определяет силу в
каждой точке поля: F= ∇П.
функция П называется потенциальной
функцией или потенциалом. В случае
когда потенциал не зависит от времени,
т.е. П=П(x,y,z),
потенциальное поле оказывается
стационарным, а его силы – консервативными.
В этом случае П(x,y,z)=
-U(x,y,z).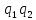 /
/ .
Поле сил, обладающее такими свойствами,
называется центральным. Если во всех
точках поля силы, действующие на
частицу, одинаковы по величине и
направлению (F=const),
поле называется однородным. Поле,
изменяющееся со временем, называется
нестационарным. Поле, остающееся
постоянным во времени, называют
стационарным. Для стационарного поля
может оказаться, что работа, совершаемая
над частицей силами поля, зависит лишь
от начального и конечного положения
частицы и не зависит от пути, по которому
двигалась частица. Силы, обладающие
таким свойством, называются
консервативными. Из независимости
работы консервативных сил от пути
вытекает, что работа таких сил на
замкнутом пути равна нулю. Не каждая
сила зависящая только от координат
точки, является консервативной.
Рассмотрим пример: пусть компоненты
силы определяются формулами
.
Поле сил, обладающее такими свойствами,
называется центральным. Если во всех
точках поля силы, действующие на
частицу, одинаковы по величине и
направлению (F=const),
поле называется однородным. Поле,
изменяющееся со временем, называется
нестационарным. Поле, остающееся
постоянным во времени, называют
стационарным. Для стационарного поля
может оказаться, что работа, совершаемая
над частицей силами поля, зависит лишь
от начального и конечного положения
частицы и не зависит от пути, по которому
двигалась частица. Силы, обладающие
таким свойством, называются
консервативными. Из независимости
работы консервативных сил от пути
вытекает, что работа таких сил на
замкнутом пути равна нулю. Не каждая
сила зависящая только от координат
точки, является консервативной.
Рассмотрим пример: пусть компоненты
силы определяются формулами
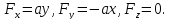 эта
сила имеет модуль равный F=ar,
и направлена по касательной к окружности
радиуса r.
Для силы такой величины и направления:
эта
сила имеет модуль равный F=ar,
и направлена по касательной к окружности
радиуса r.
Для силы такой величины и направления:

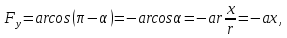 что совпадает с первоначальными
значениями. Возьмем замкнутый путь в
виде окружности радиуса
что совпадает с первоначальными
значениями. Возьмем замкнутый путь в
виде окружности радиуса
 с центром в начале координат. Работа
на этом пути равна F*2πr=ar*2πr=2πa
с центром в начале координат. Работа
на этом пути равна F*2πr=ar*2πr=2πa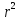 ,
т.е. отлична от нуля. Следовательно
сила не консервативна. Типичной не
консервативной силой является сила
трения. Т.к. сила трения и скорость
имеют противоположные нпаравления,
работа силы трения на каждом участке
пути отрицательна. Поэтому и на
замкнутом пути работа будет отрицательна.
Следовательно сила трения не
консервативна.
,
т.е. отлична от нуля. Следовательно
сила не консервативна. Типичной не
консервативной силой является сила
трения. Т.к. сила трения и скорость
имеют противоположные нпаравления,
работа силы трения на каждом участке
пути отрицательна. Поэтому и на
замкнутом пути работа будет отрицательна.
Следовательно сила трения не
консервативна.
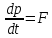 F-сила
, m-масса,
v-линейная
скорость , а-линейное ускорение,
р-импульс
F-сила
, m-масса,
v-линейная
скорость , а-линейное ускорение,
р-импульс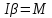
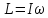
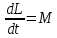
 L-момент
импульса
L-момент
импульса
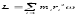 ,
где суммирование производится по всем
материальным точка системы. Величину
,
как одинаковую для всех материальных
точек, можно вынести из под знака
суммы, тогда получится
,
где суммирование производится по всем
материальным точка системы. Величину
,
как одинаковую для всех материальных
точек, можно вынести из под знака
суммы, тогда получится
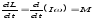 ,
,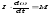 или
или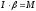
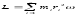 ,
где суммирование производится по всем
материальным точка системы. Величину
,
как одинаковую для всех материальных
точек, можно вынести из под знака
суммы, тогда получится
,
где суммирование производится по всем
материальным точка системы. Величину
,
как одинаковую для всех материальных
точек, можно вынести из под знака
суммы, тогда получится
 ,
,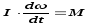 или
или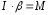 .
.  , где
R
- расстояние между осью вращения и
, где
R
- расстояние между осью вращения и
 ,
(3.5) (3.5)
,
(3.5) (3.5)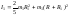 (3.6)
(3.6)
 .
(3.7) (
.
(3.7) ( (3.8)
(3.8) .
(3.9)
.
(3.9)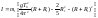 .
(3.10)
.
(3.10)
 не представляет труда. Действительно,
измеряя время t,
в течение которого груз из состояния
покоя опустится на расстояние h,
можно легко найти ускорение груза
а, в проекции на координатную ось,
совпадающую с направлением движения:
не представляет труда. Действительно,
измеряя время t,
в течение которого груз из состояния
покоя опустится на расстояние h,
можно легко найти ускорение груза
а, в проекции на координатную ось,
совпадающую с направлением движения: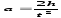 ,которое связано с угловым ускорением
(при отсутствии проскальзывания
нити относительно обода шкива) очевидным
соотношением
,которое связано с угловым ускорением
(при отсутствии проскальзывания
нити относительно обода шкива) очевидным
соотношением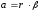 , где r
- радиус шкива
, где r
- радиус шкива ,
(3.5) (3.5)
,
(3.5) (3.5)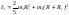 (3.6)
(3.6)
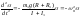 .
(3.7) (
.
(3.7) ( (3.8)
(3.8) .
(3.9)
.
(3.9)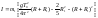 .
(3.10)
.
(3.10) .
. 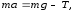
 ,
,
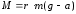
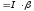 (
(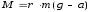 )
)
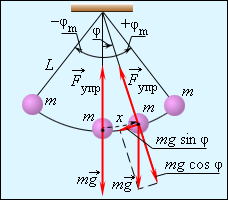
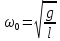
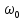 – период
– период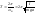 (5.7)
Число колебаний в единицу времени
называется
частотой и
обозначается .
Тогда=1/T Круговой
(или циклической) частотой называется
число колебаний за время 2
секунд, то есть круговая частота
равна:
(5.7)
Число колебаний в единицу времени
называется
частотой и
обозначается .
Тогда=1/T Круговой
(или циклической) частотой называется
число колебаний за время 2
секунд, то есть круговая частота
равна: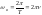 .Из сравнения с формулой (5.7) видно,
что введенная нами выше величина 0
есть
ни что иное, как круговая частота.Сравнивая
выражение (5.7)
с формулой для периода колебаний
математического маятника
.Из сравнения с формулой (5.7) видно,
что введенная нами выше величина 0
есть
ни что иное, как круговая частота.Сравнивая
выражение (5.7)
с формулой для периода колебаний
математического маятника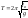 ,(5.8)
можно сделать вывод, что математический
маятник, у которого длина
,(5.8)
можно сделать вывод, что математический
маятник, у которого длина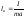 , будет иметь тот же период колебаний,
что и данный физический маятник
Величина l0
называется приведенной длиной
физического маятника.
, будет иметь тот же период колебаний,
что и данный физический маятник
Величина l0
называется приведенной длиной
физического маятника.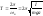 . получим
зависимость периода Т колебаний
физического маятника от расстояния
а между точкой подвеса «О» и центром
масс «С»:
. получим
зависимость периода Т колебаний
физического маятника от расстояния
а между точкой подвеса «О» и центром
масс «С»:
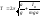
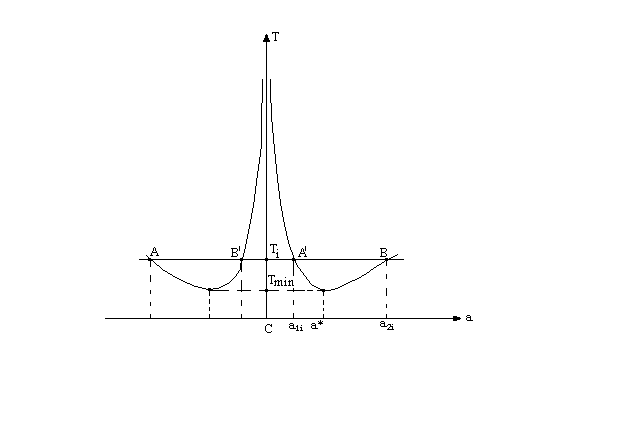
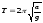 .
.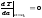 .
.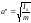 ,
,
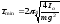

 Asin(ωt
+ φ).
Asin(ωt
+ φ).