25. Определение отрезка, теорема об отрезке.

Отрезок прямой — это множество ( часть прямой), состоящее из двух различных точек и всех точек, лежащих между ними. Отрезок прямой, соединяющий две точки A и B(которые называются концами отрезка), обозначается следующим образом — [A;B]. Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок AB». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как |AB|.

ТЕОРЕМА:

Отрезок АВ состоит из точек Х, для которых справедливо равенство: ,

где s – любое число из .

26. Дайте определение гиперплоскости в Rⁿ. Каково минимальное число к точек в пространстве R³, через которые можно провести единственную гиперплоскость, ответ обосновать.

Плоскость размерности (n-1) в Rⁿ называется гиперплоскостью. В пространстве R³ единственную плоскость можно провести через 3 точки. это так, поскольку гиперплоскость в трех мерном пространстве – это обычная плоскость, а плоскость в R³ задается уравнением: Ax+By+Cz+D=0, где (x;y;z) – координаты точки принадлежащей плоскости. Плоскость в R³ задается 3 точками.

Пусть k – натуральное число, А – фиксированная точка в n-мерном пространстве Т и - набор линейно независимых векторов из линейного пространства V. Множество точек Х вида ,

где - любые числа, называется k-мерной плоскостью в Т.

Плоскости размерности n-1 носят название гиперплоскостей.

27. Определение и свойства выпуклого множества.

Множество F подмножества Аⁿ называется выпуклым, если вместе с любыми двумя своими точками А и В оно содержит весь отрезок АВ. а) Выпуклое множество, имеющее вершину-∆. б)Выпуклое множество, не имеющее вершины - круг. Неограниченное выпуклое множество может иметь вершину. Множество точек линейного пространства, удовлетворяющих линейному неравенству, является выпуклым. Доказательство: Пусть полупространство П задано неравенством Рассмотрим

Докажем, что

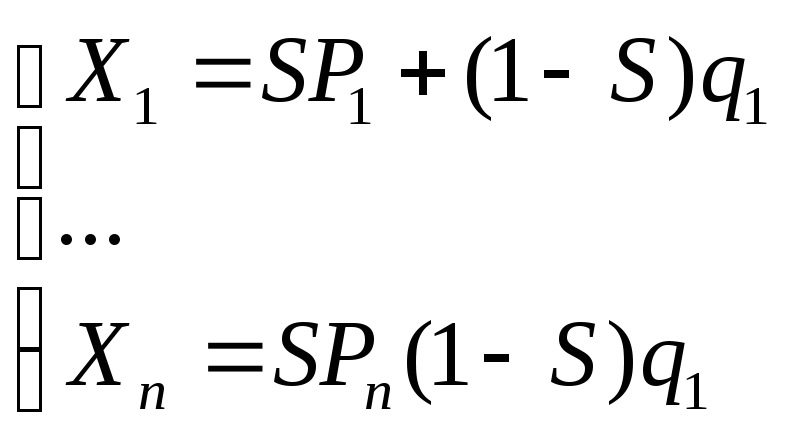
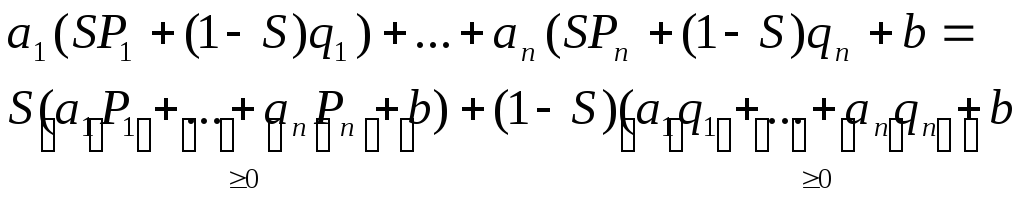
(1). Значит, (1)≥0 и

28. Дайте определение кривой второго порядка. Напишите канонические уравнения эллипса, параболы и гиперболы.

Кривой второго порядка на плоскости А² называется множество точек М(х;у), координаты которых удовлетворяют уравнению вида а11х²+2а12ху+а22у² +2а10х+2а01у+а00=0, где а11, а12, а22, а10, а01, а00 – некоторые действительные числа неравные нулю одновременно.

Каноническое уравнение эллипса: x²/a²+y²/b²=1, ab (b²=a²-c², a0)

Каноническое уравнение параболы: y²=2px

Каноническое уравнение гиперболы: x²/a²-y²/b²=1, b=(c²-a²)

29. Понятие канонической и стандартной задач линейного программирования.

Задача линейного программирования (ЛП), как уже ясно из сказанного выше, состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях.

Общая форма задачи имеет вид: найти при условиях

где

Здесь и далее нам удобнее считать с и а_і вектор - строками, а x и b=(b₁,...,b_m)^T - вектор столбцами.

Наряду с общей формой широко используются также каноническая и стандартная формы. Как в канонической, так и в стандартной форме

т.е. все переменные в любом допустимом решении задачи должны принимать неотрицательные значения (такие переменные принято называть неотрицательные в отличие от так называемых свободных переменных, на область значений которых подобное ограничение не накладывается). Отличие же между этими формами состоит в том, что в одном случае I₂ = 0, а в другом - I₁ = 0.

Задача ЛП в канонической форме:

	(2.1)
	(2.2)

(2.3)

Задача ЛП в стандартной форме:

В обоих случаях А есть матрица размерности m x n, i-я строка которой совпадает с вектором а_i.

Квадратичная форма имеет канонический вид, если она не содержит произведений переменных.

Квадратичная форма имеет нормальный вид, если все коэффициенты при квадратах по модулю равны 1. Наиболее простой способ приведения квадратичных форм к нормальному виду – метод Лагранжа.

30. Первая теорема двойственности.

Если исходная задача имеет оптимальное решение, то и двойственная ей также имеет оптимальное решение. При этом оптимальные решения целевых функций обеих задач равны, т.е. .

Вторая теорема двойственности

Оптимальные решения пары двойственных задач связаны между собой след. равенствами:

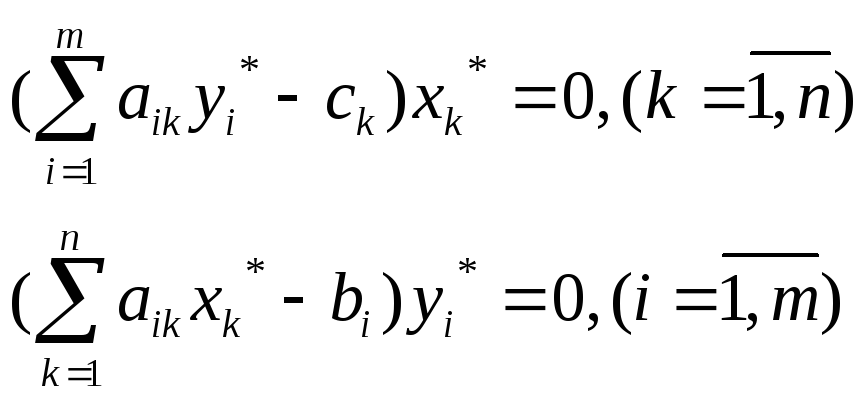
Решение двойственной ЗЛП можно получить из последней симплексной таблицы исходной задачи по формуле , где -вектор-строка, координаты которого равны коэффициентам целевой функции исходной задачи при базисных переменных последней симплексной таблицы, а В^-1 – матрица, составленная из столбцов, соответствующих базисным переменным в первой таблице.

2способ:- вектор-строка, координаты которого равны значениям оценочной строки последней таблицы, соответствующий базисным переменным исходной таблицы, а -вектор-строка, координаты которого равны коэффициентам целевой функции при базисных переменных исходной таблицы.

Исходная задача:

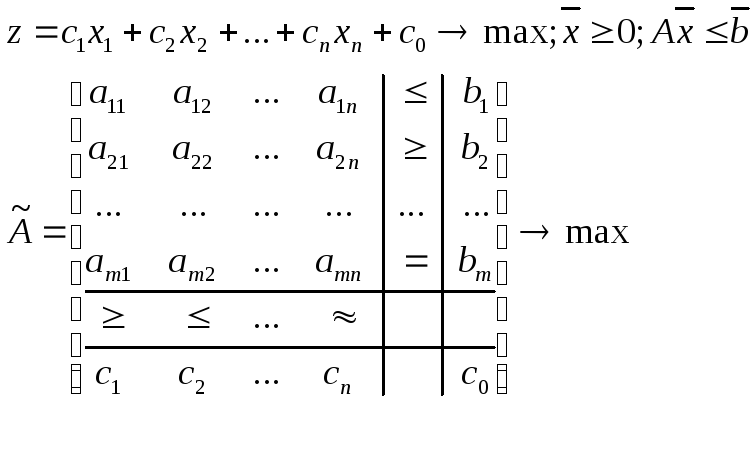
Двойственная задача: