Теорема Роля

Если функция у = f(x) :

1. Определена и непрерывна в замкнутом промежутке [а; b],

2. дифференцируема в открытом промежутке (а;b)

3) f(a)=f(b)

то существует хотя бы одна такая точка с, производная функции в которой равна нулю: f'(с) = 0

Доказательство:

Пусть f(x)=A, A-const.

Пусть =>

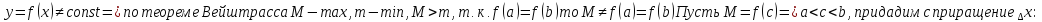
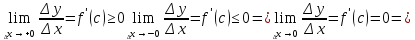
Теорема Лагранжа.

Если функция y=f(x)удовлетворяет условиям:

1) Определена и непрерывна в замкнутом промежутке [a;b],

2) дифференцируема на открытом промежутке (a;b),

то внутри интервала существует хотя бы одна такая точка с |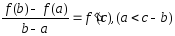

Доказательство:

Рассмотрим вспомогательную функцию . (1)

Функция F(x) непрерывна на [a,b], дифференцируема на (a,b). Подберём (2)

Из условия (1) и (2) 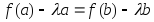. 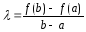, при этом 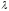по теореме Роля существует 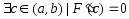. Так как , то

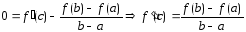
Теорема Коши

Пусть f(x) и g(x) удовлетворяют трем условиям:

1)f(x)и g(x)непрерывны на (a;b),

2) f(x)и g(x) дифференцируема на (a;b),

3),

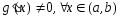То найдётся точка :

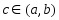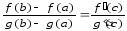
Доказательство:

Заметим, что g(a)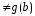, так как если бы g(a)=g(b), то по теореме Роля 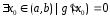- это неверно по условию 3 пункта определения. Рассмотрим |

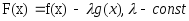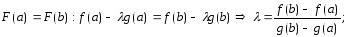
F(x) удовлетворяет теореме Роля. Поэтому для

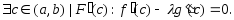
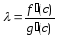, подставим :

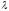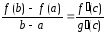
Теорема о дифференцируемости параметрически заданной функции.

Если функция аргумента задана параметрически , дифференцируются, причем 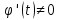, то производная этой функции по переменной вычисляется по формуле:

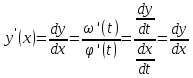
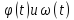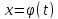
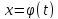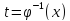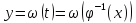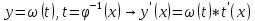
Доказательство: Предположим, что дифференцируются и имеет обратную функцию , тоже дифференцируема. Тогда , считая промежуточным аргументом. Продифференцируем итак,

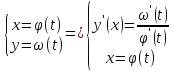
Правило Лопиталя для неопределённости вида 0/0

Пусть f(x)и g(x)удовлетворяет 3 условиям:

1)функция f(x), g(x)определены и дифференцируемы в некоторой ů(∙)Xo

2)

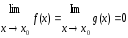
3)

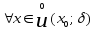
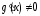
4)

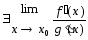
Тогда существует

Доказательство:

Пусть 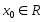и

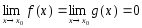
1) Пусть

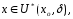
Для :

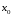• f(x) и 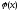непрерывны в точке 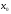. Тогда по условию (2)

• есл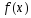и и 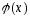имеет разрыв в точке 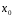, тогда 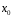- точка разрыва 1 рода.

Доопределим 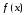и

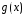
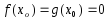
2) Пусть 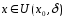. Рассмотрим f(x) и g(x) на 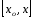. 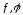удовлетворяют условиям теоремы Коши:

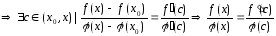
Рассмотрим 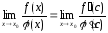, при

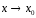
Аналитические признаки строгой монотонности (достаточные условия строгой монотонности)

Определение: Функцию f(x), x принадлежит Х, называют возрастающей (или убывающей) на множестве Х и пишут f ( или f ), если для любых х1 принадлежащих Х и х2 принадлежащих Х, таких что х1<х2, выполняется неравенство f(x1)<=f(x2) (меньше либо равно) и соответственно f(x1)>=f(x2) (больше либо равно).

Возрастающие функции называются монотонными.

Если из нер-ва х1<x2 ,х1 принадлежит Х , х2 принадлежит Х , следует что f(x1)< f(x2) ( или соответственно f(x1)>f(x2)) , то функцию f будут называть строго возрастающей или строго убывающей) и пишут f ( или соответственно f ). Строго возрастающие функции и строго убывающие функции называются строго монотонными. Если функция f (строго) возрастает на множестве Х, то функция –f (строго) убывает на этом множестве.

Верхней гранью sup(f) функции f(x), x принадлежит Х , (или, в другой записи, sup(f) ), называется верхняя грань значений этой функции на множестве ее задания Х.

Первый достаточный признак локального экстремума.

Теорема: Пусть функция задана в некоторой окрестности точки х0 (х нулевое) . Если точка х0 является точкой экстремума функции f, то ее производная равна 0 или не существует.

Действительно, производная в точке х0 либо существует , либо нет. Если она существует, то по теореме Ферма она равна 0.

Оба случая , указанных в теореме , могут быть реализованы. Например, в точке х = 0 , у = х^2 (х в квадрате) и у = х (модуль х! ) имеют строгий минимум, причем у первой из них производная в этой точке существует и равна 0, а у второй – не существует.

Отметим , что условия равенства нулю производной или ее несуществования в данной точке, будучи необходимыми условиями экстремума , не являются достаточными условиями для наличия экстремума в этой точке. Например функции f(x) = x^3 производная равна 3х^2 в точке х = 0 равна 0 , а экстремума в этой точке нет.