
- •1. Понятие экстремума функции.
- •2. Формула Тейлора.
- •4. Теорема Коши.
- •5. Правило Лопиталя ( раскрытие неопределенностей).
- •10.Замена переменных в определенном интеграле
- •11. Свойства непрерывных функций, заданных на сегменте.
- •12. Определенный интеграл.
- •13. Понятие дифференцируемости.
- •14. Дифференциал.
- •15. Точки перегиба графика функции.
- •16.Вогнутость и выпуклость графика функции
- •17.Вычисление площади криволинейного сектора
- •18.Длина дуги
- •19. Теорема Ролля.
- •20. Теорема Лагранжа.
- •22. Точки разрыва функции одной переменной.
- •Классификация точек разрыва функции.
- •23. Neopredelennyi integral I pervoobraznaya
- •24. Cвойства непрерывных функций, заданных на сегменте
- •25. Интеграл Римана.
- •26. Существование первообразной непрерывной функции.
- •1) Докажем, что
- •27. Вычисление площади криволинейной трапеции.
- •28. Свойства непрерывных на отрезке функций.
- •29. Вычисление объема тела.
- •30. Вычисление площади поверхности тел вращения.
13. Понятие дифференцируемости.
Функция
 называется дифференцируемой в данной
точке
называется дифференцируемой в данной
точке
 ,
если приращение
,
если приращение
 этой
этой
функции
в точке
 ,
соответствующее приращению аргумента
,
соответствующее приращению аргумента
 ,
может быть представлено в виде
,
может быть представлено в виде
 (5.9)
(5.9)
где
А — некоторое число, не зависящее от
 ,
а
,
а
 – функция аргумента
– функция аргумента
 ,
являющаяся бесконечно малой при
,
являющаяся бесконечно малой при
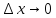 .
.
Заметим,
что функция
 может принимать в точке
может принимать в точке
 какое угодно значение (при этом в этой
точке остается справедливым представление
(5.9)). Ради определенности можно положить
какое угодно значение (при этом в этой
точке остается справедливым представление
(5.9)). Ради определенности можно положить
 .
.
Так
как произведение двух бесконечно малых является бесконечно малой более высокого
порядка, чем
является бесконечно малой более высокого
порядка, чем
 , т. е.
, т. е.
 , то формулу (5.9) можно переписать в виде
, то формулу (5.9) можно переписать в виде

Теорема
1. Для того чтобы функция
 являлась дифференцируемой в данной
точке
являлась дифференцируемой в данной
точке
 ,
необходимо и достаточно, чтобы она
имела в этой точке конечную производную.
,
необходимо и достаточно, чтобы она
имела в этой точке конечную производную.
Доказательство. 1) Необходимость.
Пусть
функция
 дифференцируема в данной точке
дифференцируема в данной точке
 ,
т. е. ее приращение
,
т. е. ее приращение
 в этой точке представимо в виде (5.9).
Предположив, что
в этой точке представимо в виде (5.9).
Предположив, что
 и поделив равенство (5.9) на
и поделив равенство (5.9) на
 ,
получим
,
получим
 (5.10)
(5.10)
Из
равенства (5.10) вытекает существование
производной, т. е. предельного значения
 .
.
2)
Достаточность. Пусть функция
 имеет в данной точке
имеет в данной точке
 конечную производную, т. е. существует
предельное значение
конечную производную, т. е. существует
предельное значение
 (5.11)
(5.11)
В
силу определения предельного значения
функция
 аргумента
аргумента
 является бесконечно малой при
является бесконечно малой при
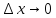 , т. е.
, т. е.
 (5.12)
(5.12)
Где
 . Представление (5.12) совпадает с
представлением (5.9), если обозначить
через А не зависящее от
. Представление (5.12) совпадает с
представлением (5.9), если обозначить
через А не зависящее от
 число
число
 .
Тем самым доказано, что функция
.
Тем самым доказано, что функция
 дифференцируема
в точке
дифференцируема
в точке .
.
14. Дифференциал.
Дифференциалом
функции
 в данной точке
в данной точке
 ,
соответствующим приращению аргумента
,
соответствующим приращению аргумента
 ,
называют главную линейную относительно
,
называют главную линейную относительно
 часть приращения этой функции в точке
часть приращения этой функции в точке
 .
.
 (5.14)
(5.14)

![]()

15. Точки перегиба графика функции.
Точка
 графика функции
графика функции
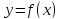 называется точкой перегиба этого
графика, если существует такая окрестность
точки с оси абсцисс, в пределах которой
график функции
называется точкой перегиба этого
графика, если существует такая окрестность
точки с оси абсцисс, в пределах которой
график функции
 слева и справа от с имеет разные
направления выпуклости.
слева и справа от с имеет разные
направления выпуклости.
Первое
достаточное условие перегиба. Пусть
функция
 имеет вторую производную в некоторой
окрестности точки с и
имеет вторую производную в некоторой
окрестности точки с и
 .
Тогда, если в пределах указанной
окрестности вторая производная
.
Тогда, если в пределах указанной
окрестности вторая производная
 имеет разные знаки слева и справа от
с, то график этой функции имеет перегиб
в точке
имеет разные знаки слева и справа от
с, то график этой функции имеет перегиб
в точке
 .
.
Доказательство.
Заметим, во-первых, что график функции
 имеет касательную в точке
имеет касательную в точке
 ,
ибо из условий теоремы вытекает
существование конечной производной
,
ибо из условий теоремы вытекает
существование конечной производной
 .
Далее, из того, что
.
Далее, из того, что
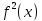 слева и справа от с имеет разные знаки,
и из теоремы «Если функция
слева и справа от с имеет разные знаки,
и из теоремы «Если функция
 имеет на интервале
имеет на интервале
 конечную вторую производную и если эта
производная неотрицательна (неположительна)
всюду на этом интервале, то график
функции
конечную вторую производную и если эта
производная неотрицательна (неположительна)
всюду на этом интервале, то график
функции
 имеет на интервале
имеет на интервале

выпуклость, направленную вниз (вверх)» заключаем, что направление выпуклости слева и справа от с является различным.
Второе
достаточное условие перегиба. Если
функция
 имеет в точке с конечную третью
производную и удовлетворяет в этой
точке условиям
имеет в точке с конечную третью
производную и удовлетворяет в этой
точке условиям
 ,
,
 ,
то график этой функции имеет перегиб
в точке M(c,f(c)).
,
то график этой функции имеет перегиб
в точке M(c,f(c)).
Доказательство.
Из условия
 и из теоремы «Если функция
и из теоремы «Если функция
 дифференцируема в
дифференцируема в
точке
с и
 ,
то эта функция возрастает (убывает) в
точке с» вытекает, что функция
,
то эта функция возрастает (убывает) в
точке с» вытекает, что функция либо возрастает, либо убывает в точке
с. Так как
либо возрастает, либо убывает в точке
с. Так как ,
то и в том, и в другом случае найдется
такая окрестность точки с, в пределах
которой
,
то и в том, и в другом случае найдется
такая окрестность точки с, в пределах
которой
 имеет разные знаки слева и справа от
с. Но тогда по предыдущей теореме график
функций
имеет разные знаки слева и справа от
с. Но тогда по предыдущей теореме график
функций
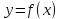 имеет перегиб в точке M(c,f(c))
.
имеет перегиб в точке M(c,f(c))
.
