
- •Оглавление
- •Часть 1. Расчет параметров посадки отверстия и вала.
- •Часть 2 Метод полной взаимозаменяемости Прямая задача
- •Способ полной взаимозаменяемости обратная задача
- •Способ вероятностный Прямая задача
- •Способ вероятностный Обратная задача
- •Часть 3 Обработка результатов многократных измерений
- •Список использованных источников
Способ вероятностный Обратная задача
Сведем данные для расчета в табл.4.
1. Номинальное значение замыкающего размера
![]()
2. Среднее отклонение замыкающего размера
![]()
3. Допуск замыкающего размера
![]()
Предельные отклонения замыкающего размер
![]()
С![]() равниваем
полученные результаты с заданными
равниваем
полученные результаты с заданными
Следовательно, изменения предельных отклонений составляющих размеров
не требуется.
Таблица 4
|
Обоз. размеров |
Размер |
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
-0,06 |
0,12 |
+0,2 |
0,012 |
-0,048 |
-0,048 |
0,12 |
0,0144 |
|
|
|
+1 |
0,717 |
0,29 |
+0,2 |
0,029 |
+0,746 |
+0,746 |
0,29 |
0,0841 |
|
|
|
+1 |
-0,06 |
0,12 |
+ 0,2 |
0,012 |
-0,048 |
-0,048 |
0,12 |
0,0144 |
|
|
|
-1 |
0 |
0,25 |
0 |
0 |
0 |
0 |
0,25 |
0,0625 |
Часть 3 Обработка результатов многократных измерений
В табл.1 приведены 100 независимых числовых значений результата измерения X, каждое из которых повторилось m раз. Доверительная вероятность P=0,96
Табл. 1
|
X, В |
43.87 |
43.9 |
43.96 |
43.98 |
43.99 |
44 |
44.01 |
44.03 |
44.05 |
44.06 |
44.08 |
|
m |
1 |
1 |
1 |
1 |
2 |
1 |
1 |
2 |
2 |
3 |
3 |
|
X, В |
44.09 |
44.1 |
44.11 |
44.12 |
44.13 |
44.15 |
44.16 |
44.17 |
44.18 |
44.19 |
44.22 |
|
m |
2 |
1 |
3 |
1 |
1 |
4 |
2 |
3 |
2 |
1 |
2 |
|
X, В |
44.23 |
44.24 |
44.25 |
44.28 |
44.29 |
44.3 |
44.31 |
44.32 |
44.33 |
44.34 |
44.35 |
|
m |
1 |
3 |
1 |
2 |
1 |
4 |
5 |
1 |
2 |
1 |
3 |
|
X, В |
44.37 |
44.39 |
44.41 |
44.42 |
44.43 |
44.44 |
44.45 |
44.46 |
44.47 |
44.48 |
44.51 |
|
m |
2 |
3 |
2 |
1 |
4 |
1 |
3 |
2 |
1 |
2 |
3 |
|
X, В |
44.53 |
44.57 |
44.59 |
44.61 |
44.62 |
44.7 |
44.75 |
44.82 |
44.85 |
|
m |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
1 |
1 |
1.Определяем
среднее арифметическое и стандартное
отклонение для данных табл.1: 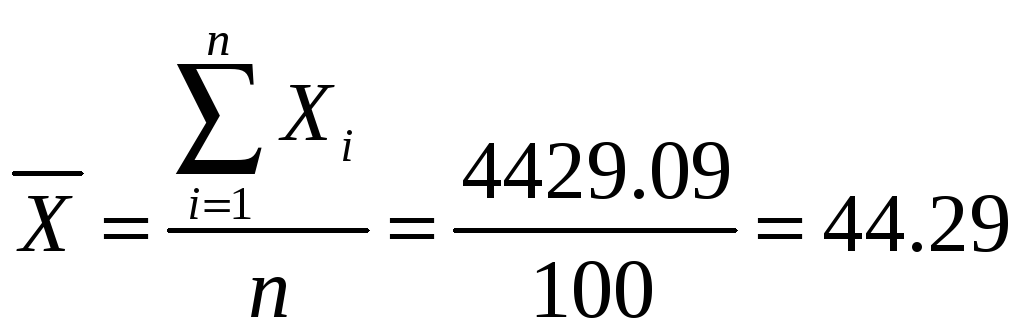 ;
; ![]()
 .
.
2. С помощью правила « трех сигм» проверяем наличие или отсутствие промахов.
![]()
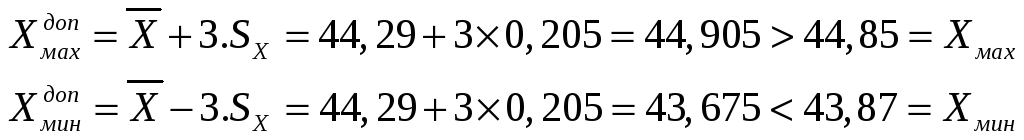
Таким
образом, ни один из результатов не
выходит за границы интервала![]() ,
следовательно, с вероятностью 0,9973
гипотеза
об
отсутствии
грубых погрешностей принимается.
,
следовательно, с вероятностью 0,9973
гипотеза
об
отсутствии
грубых погрешностей принимается.
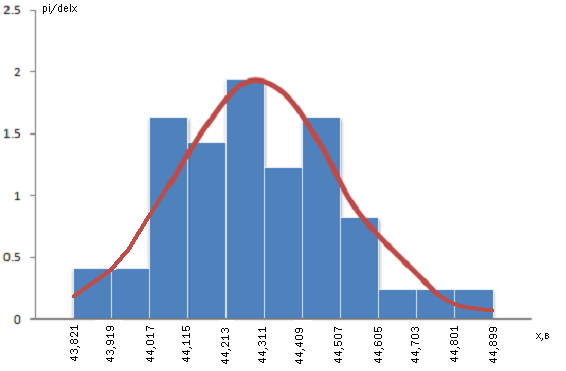
3. Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.
Для этого, чтобы построить гистограмму, необходимо результаты отдельных измерений расположить в так называемый вариационный ряд по возрастанию их численных значений( в рассматриваемом примере эта процедура уже проделана и представлена табл.1)
Участок
оси абсцисс, на котором располагает
вариационный ряд значений физической
величины, разбивается на k одинаковых
интервалов![]() .
Выбор числа интервалов k=10 :
.
Выбор числа интервалов k=10 :
![]() .
.
Выбор начала первого интервала в точке 43,821, тогда конец последнего(11-го) интервала окажется в точке 44,899
Затем
для каждого интервала подсчитывается
количество результатов
![]() ,
попавших в данный интервал и определяется
,
попавших в данный интервал и определяется
![]()
(Результаты приведены в табл.2)
Общее число интервалов становится равным 8.
4. Проверка нормальности закона распределения по критерию Пирсона.
Если выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используется функция Лапласа:
![]()
![]() ,
,
![]() и
и
![]() определяем по таблице.
определяем по таблице.
Найдя
таким образом значения Рi
для каждого
интервала ki
, заполним
соответствующие ячейки таблицы 2, а
затем рассчитаем значение
![]() -- критерия
для каждого интервала и, наконец суммарное
значение
-- критерия
для каждого интервала и, наконец суммарное
значение
![]() :
: ![]()
Определим
табличное значение
![]() ,
задавшись доверительной вероятностью
0,96 и вычислив по формуле r=k-3 число
степеней свободы:
,
задавшись доверительной вероятностью
0,96 и вычислив по формуле r=k-3 число
степеней свободы:
r =k-3=10-3 =7 ;
![]()
Таким образом, с вероятностью 0,96 гипотеза о нормальности распределения вероятности результата измерения принимается.
5.
В тех же координатах , что и гистограмма
, следует построить теоретическую
кривую плотности вероятности . Для этого
рассчитываются значения плотности
вероятности для середина каждого
интервала pi=Pi/![]() и откладываются как ординаты из середины
соответствующих интервалов , полученные
точки соединяют плавной кривой ,
симметричной относительно математического
ожидания .
и откладываются как ординаты из середины
соответствующих интервалов , полученные
точки соединяют плавной кривой ,
симметричной относительно математического
ожидания .
6. Представление результатов в виде доверительного интервала.
Для этого определим стандартное отклонение среднего арифметического по формуле:
![]()
Закон
распределения вероятности для среднего
арифметического
считаем нормальным (что следует из
нормальности распределения самой
измеряемой
величины), тогда доверительный интервал
определяется по выражению (![]() )
при доверительной вероятности 0,96.
Этому значению соответствует аргумент
функции Лапласа t = 2,26
)
при доверительной вероятности 0,96.
Этому значению соответствует аргумент
функции Лапласа t = 2,26
![]()
В случае, если закон распределения вероятности для среднего арифметического считается неизвестным, то относительный доверительный интервал рассчитывается в соответствии с неравенством Чебышева :
![]() ;
t=5
;
t=5
![]()
Как видно из сравнения результатов, неизвестность закона распределения вероятности приводит к расширению доверительного интервала, то есть к увеличению дефицита измерительной информации
табл.2
|
i |
Xi-1 |
Xi |
m |
|
ti-1 |
ti |
Фi-1 |
Фi |
Pi |
|
|
1 |
43.821 |
43.919 |
2 |
|
|
|
|
|
|
|
|
2 |
43.919 |
44.017 |
6 |
0.408163 |
-2.2878 |
-1.33171 |
-0.4887 |
-0.4082 |
0.0805 |
0.000311 |
|
3 |
44.017 |
44.115 |
16 |
1.632653 |
-1.33171 |
-0.85366 |
-0.4082 |
-0.3023 |
0.1059 |
2.763749 |
|
4 |
44.115 |
44.213 |
14 |
1.428571 |
-0.85366 |
-0.37561 |
-0.3023 |
-0.148 |
0.1543 |
0.132528 |
|
5 |
44.213 |
44.311 |
19 |
1.938776 |
-0.37561 |
0.102439 |
-0.148 |
0.0398 |
0.1878 |
0.002577 |
|
6 |
44.311 |
44.409 |
12 |
1.22449 |
0.102439 |
0.580488 |
0.0398 |
0.219 |
0.1792 |
1.955714 |
|
7 |
44.409 |
44.507 |
16 |
1.632653 |
0.580488 |
1.058537 |
0.219 |
0.3554 |
0.1364 |
0.408328 |
|
8 |
44.507 |
44.605 |
8 |
0.816327 |
1.058537 |
1.536585 |
0.3554 |
0.4382 |
0.0828 |
0.009469 |
|
9 |
44.605 |
44.703 |
4 |
|
|
|
|
|
|
|
|
10 |
44.703 |
44.801 |
1 |
0.238095 |
1.536585 |
2.970732 |
0.4382 |
0.4986 |
0.0604 |
0.152583 |
|
11 |
44.801 |
44.899 |
2 |
|
|
|
|
|
|
|
Заключение
Рассмотрев основные аспекты государственного контроля и надзора за соблюдением требований государственных стандартов, становится очевидным, что государственный контроль над единством измерений и соблюдений стандартов необходим для обеспечения соответствия нормам стандартов всех отраслей науки, промышленности и хозяйства. Проведя расчеты по составлению размерных цепей, посадок и статистического анализа многократных измерений, становится ясным необходимость и достаточность для этого математических навыков.
