4. Равномерное движение

В зависимости от того, как изменяются со временем скорость и ускорение материальной точки, ее движение может быть разделено на несколько видов. Простейшим является случай движения с постоянной по модулю скоростью – равномерное движение.

Рассмотрим равномерное движение материальной точки с постоянной по модулю скоростью const. по произвольной траектории. Из определения модуля скорости следует, что элементарный путь ds, который материальная точка проходит за время dt, находится как:

.

Интегрируя, получим закон зависимости пройденного пути от времени наблюдения t:

Константу интегрирования C определим из начальных условий. Если в начале наблюдения при t = 0 путь материальной точки , тогда , а закон зависимости пути от времени наблюдения принимает вид:

Если в момент времени t = 0 пройденный путь, тогда

.

Равномерное движение не означает дви­жения без ускорения, поскольку при криво­линейном равномерном движении матери­альная точка обладает нормальным ускорением . Равна нулю только тангенциальная компонента ускорения, поскольку скорость не меняется по величине. Для равномерного движения

Рассмотрим равномерное движение материальной точки по окружности (Рис 1.10). Расположим начало координат в центре этой окружности. В случае равномерного движения радиус-вектор прецессирует с угловой скоростью и, согласно уравнению прецессии, Вектор скорости материальной точки также прецессирует с угловой скоростью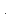Тогда вектор нормального ускорения . Применяя свойство двойного векторного произведения, получим Так как векторы и взаимно перпендикулярны, первое слагаемое равно нулю, и .

Рис. 1.10.

5. Равномерное прямолинейное движение

Пусть материальная точка движется равномерно по прямолинейной траектории. Тогда вектор мгновенной скорости остается постоянным не только по модулю, но и по направлению. Согласно определению вектора мгновенной скорости . Тогда . Интегрируя это выражение, найдём зависимость радиус-вектора движущейся материальной точки от времени наблюдения

Константу интегрирования C определим из начальных условий: если в начале наблюдения при t = 0 положение материальной точки определялось радиус-вектором (рис. 1.11), то , а зависимость радиус-вектора от времени принимает вид

.

В проекциях на оси координат

Ось x обычно проводят по траектории прямолинейного движения, тогда пройденный материальной точкой путь

Рис. 1.11.

6. Движение с постоянной тангенциальной составляющей вектора ускорения aτ.

Определим зависимость модуля скорости от времени наблюдения, используя определение тангенциальной составляющей ускорения. За промежуток времени dt изменение модуля скорости. Интегрируя, получим:

.

Константу интегрирования C определим из начальных условий: если в момент начала наблюдения при t = 0 материальная точка обладала скоростью, по модулю равной , тогда , а зависимость модуля скорости от времени наблюдения:

. (1.2)

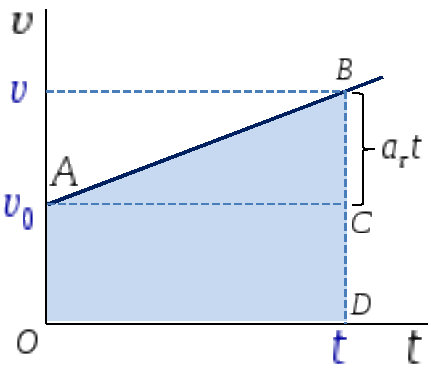
График этой зависимости показан на рисунке 1.12.

Аналогично определим зависимость пройденного пути от времени наблюдения. Из определения модуля скорости выразим элементарный путь. Интегрируя, получим

Константу интегрирования определим из начальных условий: если в момент времени t = 0 путь s = 0, тогда C = 0, а зависимость пути от времени принимает вид:

(1.3)

Рис. 1.12.

К такому же результату можно прийти, используя график зависимости скорости от времени. Путь, пройденный материальной точкой за время t, соответствует площади под графиком скорости. На рис. 1.12 эта площадь выделена цветом. Видно, что она равна сумме площадей прямоугольника OACD и треугольника АВС. Площадь прямоугольника соответствует, площадь треугольника . Таким образом,

Всю заштрихованную площадь можно также представить как площадь трапеции OABD, равную произведению полусуммы оснований и на высоту t, тогда

(1.4)

Из (1.2) выразим время, , и подставим его в (1.4), тогда

и