4. Машина вывода.

Машина вывода (интерпретатор правил) выполняет две функции:

1. Просматривает существующие факты из рабочей памяти (ее иногда называют базой данных) и правил из базы знаний и добавляет в рабочую память новые факты.

2. Определяет порядок просмотра и применения правил.

Машина вывода реализуется программой, состоящей из двух компонентов: реализации вывода и управления процессом реализации. Первый компонент работает на основе логического правила Moduns Ponens : если А и если А то В, то В.

Компонент вывода должен функционировать даже при недостатке информации. При этом полученное решение может быть неточным, но система должна продолжать работать.

Управляющий компонент выполняет следующие функции:

1. Сопоставление. Образец правила сопоставляется с имеющимися фактами.

2. Выбор. Если применимы несколько правил, то выбирается одно, наиболее подходящее по выбранному критерию.

3. Срабатывание. Если образец правила при сравнении совпал с какими-либо фактами из рабочей памяти, то правило срабатывает.

4. Действие. Рабочая память изменяется путем добавления в нее заключения сработавшего правила. Если в правой части правила имеются указания на какие-либо действия, то они выполняются.

4. Различные стратегии поиска вывода.

Продукционные правила предполагают на каждом шаге вывода просмотр всех правил (в порядке их следования) и пополнение фактов за счет выполнения активизированных правил. Такая стратегия вывода называется прямой. В этом случае имеет место рассуждение: если факты, составляющие антецедент продукции уже находятся в рабочей памяти (т.е. установлены), то и утверждения, составляющие консеквент, также заносятся в рабочую память, т.е. считаются установленными фактами.

Возможна и другая стратегия. В ней зависимость «если - то» используется в другом смысле. Пусть нам нужно вывести утверждение из консеквента некоторой продукции. Тогда проверяем, доказаны ли утверждения из антецедента этой продукции. Если доказаны, то вывод найден. В противном случае потребуется применить то же рассуждение для недоказанных утверждений из антецедента и т.д., пока все утверждения из А не будут доказаны, доказывая тем самым утверждения из В. Таким образом, активизируются те продукции, консеквенты которых содержат утверждения, подлежащие выводу. Эта стратегия поиска логического вывода называется обратной.

Как прямая, так и обратная стратегии, в свою очередь, делятся на параллельную и последовательную. Они отличаются друг от друга методами перебора. При параллельной стратегии все возможные варианты вывода рассматриваются параллельно. Этот способ не требует возвратов, реализации «бектрекинга». Напротив, последовательная стратегия предусматривает последовательный перебор вариантов с использованием бектрекинга. Эта стратегия, по сути, эквивалентна обходу дерева. Приведем пример, иллюстрирующий два варианта стратегий: прямой параллельный и обратный последовательный.

Пример 6.

Пусть в нашей БЗ используются утверждения

r, s, t, u, v, w, x, y, z.

Правила вывода, представленные в виде продукций, таковы:

1. r –> t 4) s –> u 7) w, x --> y

2. u –> t 5) r, t, v –> w 8) u, w, x --> z

3. r, u –> v 6) u, y –> w 9) r, w –> z

Будем считать, что установленными являются утверждения r и s и нашей задачей является установить, выводимо ли утверждение z.

Прямая стратегия.

Результаты работы алгоритма, реализующего прямую стратегию, можно представить в виде таблицы, состоящей из следующих столбцов: № шага, номера активизированных продукций, и факты, попадающие в базу данных в процессе работы алгоритма. Перед началом работы (шаг 0) в базу данных заносятся факты, считающиеся доказанными a priori, т.е. начальные условия. Затем активизируются все продукции, антецеденты которых состоят только из фактов, находящихся в БД. Консеквентны активизированных продукций заносятся в БД. Работа алгоритма прекращается, когда на очередном шаге в БД не будет занесен ни один новый факт. Возможен и другой вариант окончания работы: если требуется вывести указанные утверждения, работу можно закончить, когда все они попадут в БД. Ниже приведена таблица вывода утверждения z при указанных выше начальных условиях.

№№ шагов	акт. п-ла	база данных
0	-	r, s
1	1,4	r, s, t, u
2	2,3	r, s, t, u, v
3	5	r, s, t, u, v, w
4	9	r, s, t, u, v, w, z

Вывод получен.

Обратная стратегия.

Алгоритм, реализующий обратную стратегию, осуществляет построение специального дерева вывода. Построение дерева начнем с корня, который пометим утверждением, истинность которого требуется установить. Остальные вершины будем помечать левыми частями продукций (заметим, что при необходимости вывести несколько утверждений, понадобится сформировать «лес» – т.е. по одному дереву для каждого утверждения). Дуги дерева будем помечать номерами в соответствии с порядком их построения и номерами продукций в скобках. На каждом шаге требуется найти продукцию, в правой части которой находится анализируемое утверждение. На первом шаге выберем утверждение, помечающее корень. Дальнейшие шаги алгоритма проиллюстрируем выводом утверждения z в БЗ примера:

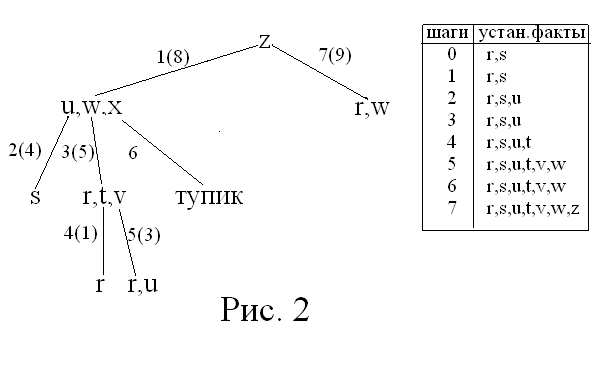
Поясним работу алгоритма. Его начальным условием является установленные a priori факты r и s. На первом шаге ищем первую продукцию, в правой части которой находится z. Это продукция 8. В стеке возвратов запоминаем, что дальнейший просмотр продукций при возврате на этот шаг следует начинать с продукции 9. Формируем вершину u,w,x и строим в нее дугу из вершины z. Из вершины u,w,x необходимо построить три вершины и три дуги по продукциям, в правых частях которых находятся утверждения u, w и x. Сначала строим первую пару – вершину s и дугу 2(4). Дуга 2(4) позволяет вывести утверждение u и занести его в список установленных фактов (БД). Затем строим пару r,t,v и дугу 3(5). r – установленный факт, а построение вершин r и r,u и дуг 4(1) и 5(3) позволяет считать выведенными факты t, v и w. Однако утверждение х в правых частях продукций отсутствует. Поэтому продолжение вывода невозможно – возник тупик и данный вариант вывода оказался непродуктивным.

Используя стек возвратов, ищем другое правило для z. Это правило 9. Применив его, завершаем вывод. В таблице в правой части рисунка 2 содержатся списки установленных фактов (содержимое БД) после каждого шага вывода.

НЕОПРЕДЕЛЕННОСТЬ ЗНАНИЙ И ДАННЫХ.

Неопределенность используемой информации в ЭС в большинстве случаев имеет два источника:

а) недостаточно полное знание предметной области;

б) неполная информация о текущей ситуации.

В практической деятельности мы сталкиваемся с ситуацией, когда имеющаяся в нашем распоряжении информация неполна, неопределенна, требует детализации и пр. Например, могут быть несколько теорий о происхождении и проявлениях того или иного явления, имеющиеся сведения могут быть недостаточно четко и формально сформулированы и пр. Примеров подобных обстоятельств молжно привести много. Наконец, даже если знания о предметной области достаточно полны, эксперт может предпочесть точным эвристические методы решения проблем.

Помимо неточных знаний неопределенность может быть внесена и неточными или ненадежными данными о конкретной ситуации. Измерительные приборы имеют ограниченную точность и не 100-процентную надежность; при анализе ситуации могут использоваться недостоверные или даже ошибочные данные.

Итак, эксперты вынуждены пользоваться неточными методами по двум главным причинам:

1. точных методов не существует;

2. точные методы существуют, но не могут применяться из-за недостаточного объема данных или невозможности их накопления по соображениям стоимости, отсутствия необходимого времени и пр.

Таким образом, неточные методы играют значительную роль впри разработке ЭС, но мнения, какие именно методы использовать, разделились. Имеются два подхода к этой проблеме: применение теории вероятностей и нечеткая логика.

ЭС и теория вероятностей.

Условная вероятность.

Условная вероятность события d при данном событии s – это вероятность наступления d при условии, что наступило s.

В традиционной теории вероятностей для вычисления условной вероятности используется формула:

P(d|s) = P(ds) / P(s) (1)

или

P(s|d) = P(ds) / P(d)

или

P(ds) = P(s|d)P(d)

Поделим обе части последней формулы на P(s) и воспользуемся первой формулой:

P(d|s) = P(s|d)P(d) / P(s). (2)

Эта формула часто называется инверсной формулой условной вероятности, она представляет правило Байеса в простейшем виде. Суть формулы в том, что условная вероятность P(d|s) может быть вычислена через «инверсную» условную вероятность P(s|d), которую мы считаем известной. Иногда P(d) называют априорной вероятностью события d, а P(d|s) –апостериорной вероятностью.

В ЭС формула (2) удобнее формулы (1). Покажем это на примере. Пусть у пациента наблюдается боль в груди и необходимо оценить вероятность у него инфаркта миокарда (учитывая, что боль в груди может быть следствием совсем другого заболевания). Итак d – и.м., s – б.г. Для вычисления искомой вероятности по формуле (1) нужно знать, сколько человек в мире страдают б.г. и сколько из них страдают б.г. потому, что больны и.м. Обычно такая информация отсутствует, особенно та, которая необходима для вычисления P(ds).

Эта трудность послужила основанием для негативной оценки роли ТВ в ИИ. Однако, существует и так называемая «субъективистская» точка зрения на ТВ, которая позволяет иметь дело с оценками вероятностей наступления событий, а не с их частотой. Например, врач-эксперт может оценить, у какой части инфарктников наблюдается боль в груди и на этом основании дать оценку условной вероятности Р(и.м.|б.г.). А оценку вероятности заболевания и.м. можно взять из публикуемой статистики.

Если имеется некое множество n симптомов S и множество m возможных заболеваний D, то для вероятности каждого заболевания d нужно использовать правило Байеса в более общей форме:

P(d|s₁…s_k) = P(s₁…s_k|d)P(d) / P(s₁…s_k).

Вычисление этой вероятности достаточно трудоемко, так как для вычисления P(s₁…s_k) нужно предварительно вычислить произведение P(s₁| s₂…s_k)P(s₂|s₃…s_k) … P(s_k). Однако если предположить, что некоторые симптомы независимы друг от друга, то объем вычислений снижается. Действительно, если s_i и s_j независимы, то P(s_i) = P(s_i|s_j), а отсюда следует, что P(s_is_j) = P(s_i)P(s_j). Если все симптомы независимы, то объем вычислений не будет существенно отличаться от случая учета одного симптома.

Наконец, если независимость симптомов теоретически не подтверждается, эксперт может воспользоваться условной независимостью, опираясь на свой профессиональный опыт. Например, если в автомобиле не работает освещение и нет горючего, то эксперт может смело сказать, что эти симптомы независимы. Но если не работает освещение и машина не заводится, то эти симптомы нельзя считать независимыми, так как они могут быть вызваны разрядкой аккумулятора.

Таким образом, использование ТВ ставит перед разработчиками ЭС следующие проблемы:

– можно предположить, что все данные (симптомы) независимы и использовать менее трудоемкие методы вычислений, но при этом достоверность результатов будет снижаться;

– для получения более достоверных результатов нужно отслеживать зависимости данных друг от друга и оперативно обновлять соответствующую информацию, т.е. использовать значительно более трудоемкие методы.

Коэффициенты уверенности.

Альтернативным подходом к оценке достоверности тех или иных заключений основан на так называемых правилах влияния, которые в общем случае можно представить так:

ЕСЛИ	пациент имеет показания и симптомы s1…sk и имеют место некоторые фоновые условия t1…tm,
ТО	Можно с уверенностью  заключить, что пациент страдает заболеванием d.

Коэффициент уверенности  принимает значения в диапазоне [-1, 1]. Если  = +1, это означает, что при соблюдении всех указанных в правиле условий эксперт абсолютно уверен в правильности заключения d. Если  = -1, это означает, что эксперт абсолютно уверен в ошибочности заключения. Значения  > 0 указывают на степень уверенности эксперта в правильности заключения, а значения  < 0 – степень уверенности в ошибочности заключения.

Формулы указанного вида применяются для того, чтобы заменить громоздкие вычисления условных вероятностей P(d|s₁…s_k) легко вычисляемой приближенной оценкой и тем самым приблизить процесс принятия решений ЭС к способу принятия решений экспертом. Пусть CF(d,s₁…s_k t₁…t_m) – коэффициент уверенности в достоверности заключения d, зависящий от коэффициентов уверенности в достоверности симптомов s₁,…,s_k и значений фоновых условий t₁,…,t_m; CF(s_i) и SF(t_j) – коэффициенты уверенности в достоверности соответствующих симптомов и фоновых условий. Тогда вычисление коэффициента уверенности в достоверности заключения вычисляется по следующей формуле:

CF(d,s₁…s_k t₁…t_m) =   min(CF(s₁), …, CF(s_k), SF(t₁), … , SF(t_m)).

НЕЧЕТКАЯ ЛОГИКА

Нечеткая логика, опирающаяся на понятие нечетких множеств, представляет альтернативу вероятностному подходу к работе с мягкими знаниями. Отнесение конкретного объекта к определенной категории в большинстве случаев не может быть категоричным: объект может обладать частью необходимых признаков, частью не обладать ими. Сами признаки могут быть размыты, например, такие как «большой», «маленький», «красивый» и т.п. Предложенная американским логиком Заде теория нечетких множеств (fuzzy set theory) представляет формализм для формирования суждений о таких объектах и соответствующих им категориях.

В классической теории множеств объект может принадлежать или не принадлежать некоторому множеству. Соответственно выражение а  А может быть либо истинным, либо ложным. Такие множества получили название жестких. В противоположность им в нечетких множествах допускается степень принадлежности объекта множеству. Эта характеристика представляется функцией f(X), где Х – некоторый объект. Функция может принимать значения в интервале [0,1]. Нечеткие множества тесно связаны с субъективным восприятием реального мира различными индивидами. Это восприятие зависит от характерологических особенностей индивидуума, его профессии, материального положения и пр. Например, рассмотрим множество быстрых автомобилей. Для владельца «Жигулей» автомобиль, развивающий предельную скорость 160 км/час, в большинстве случаев будет казаться быстрым. Для владельца «Мерседеса» критерий быстрого автомобиля будет существенно иным. Итак, если f(X) = 1, то объект Х безусловно входит в множество, для которого определена функция f. При f(X) = 0 f(X) = 1 объект безусловно не входит в множество. Все промежуточные значения функции означают степень членства объекта в множестве. Таким образом, членами нечеткого множества становятся пары (объект, степень). Например множество быстрых автомобилей может быть определено так:

FAST-CAR = { (Порше, 0.9), (Мерседес, 0.8), … , (Жигули, 0.1)}.

Нечеткая логика тесно связана с нечеткими множествами. В ней высказывания и предикаты могут принимать значения в интервале [0, 1]. При этом значения 0 и 1 соответствуют false и true классической логики, а промежуточные – степени уверенности в истинности соответствующих высказываний или предикатов. Естественно, для вычисления значений формул (например, исчисления предикатов) были разработаны соответствующие правила. Вот они:

f(X) = 1 – f(X);

f(X)  g(X) = min (f(X), g(X));

f(X)  g(X) = max (f(X), g(X)).

Приведенные операции обладают теми же свойствами, что и соответствующие операции классической логики: коммутативности, ассоциативности, взаимной дистрибутивности. Как и в классической логике к ним применим принцип композитивности, т.е. значения составных выражений вычисляются только по значениям выражений-компонентов.

Теория возможности

Нечеткая логика применяется тогда, когда мы имеем дело с нечетко очерченными понятиями. Однако, иногда мы просто не уверены в самих фактах, хотя последние являются вполне четкими. Например, на вопрос «Находится ли в настоящее время Иван в Москве?» мы можем не знать точный ответ. Здесь неопределенность заложена не в понятиях, а в самом высказывании.

Теория возможностей как раз и применяется при обработке точно сформулированных вопросов, базирующихся на неточных знаниях. Рассмотрим пример.

Пусть в ящике находятся 10 шаров, причем нам известно, что несколько из них являются красными. Какова вероятность того, что из ящика будет вынут красный шар? Очевидно, она зависит от того, какое количество красных шаров подходит под определение «несколько». Определим нечеткое множество:

SEVERAL = {(3, 0.2), (4, 0.6), (5, 1.0), (6, 1.0), (7, 0.6), (8, 0.3)}.

Здесь коэффициент, как и прежде означает субъективную степень членства объекта в множестве. Например, есть полная уверенность, что в множество SEVERAL попадают числа 5 и 6, а 3 и 8 – попадают с низкой степенью уверенности. Обозначим вероятность извлечения красного шара через P(RED). Тогда, разделив числа из множества на 10, получим следующее распределение вероятностей:

{(0.3, 0.2), (0.4, 0,6), (0.5, 1.0), (0,6, 1.0), (0.7, 0.6), (0.8, 0.3)}.