Министерство образования и науки, молодежи и спорта Украины

Ялтинский университет менеджмента

Кафедра «Программного обеспечения автоматизированных систем»

Работа допущена к защите _______________________ Научный руководитель: Богданова Л.А. . «___»___________2011г.

Работа защищена с оценкой ________________________ «___»_____________2011 г. Подписи членов комиссии ________________________

Курсовой проект

По дисциплине: «Функциональный и выпуклый анализ»

Тема: Метод простой итерации решения систем линейных алгебраических уравнений

Выполнил: студент 2 курса, гр. КН-10

Сербул Роман Сергеевич

«____»____________________2011г.

Утверждаю:

___________________

Зав. кафедрой программного

обеспечения автоматизированных систем

______________

^{(подпись)}

Ялта – 2011

Содержание

1. Введение………………………………………………………………3

2. Основные определения………………………………………………4

2.1 Определения собственного значения и собственного вектора матрицы. Пример нахождения собственных значений и собственных векторов матрицы…………………………………………………….......4

2.2. Некоторые свойства собственных значений векторов………..10

2.3 Системы линейных алгебраических уравнений………………..11

3. Методы решения систем линейных алгебраических уравнений…..12

3.1 Метод Зейделя……………………………………………………12

3.2 Метод верхних релаксаций……………………………………...14

3.3 Метод Якоби……………………………………………………...16

4. Программа на C++ для решения СЛАУ методом Якоби……….…..20

5. Заключение ………………………………………………………………………22

6. Список использованной литературы……………………………………….23

1. Введение

Численные методы являются одним из мощных математических средств решения задачи. Простейшие численные методы мы используем всюду, например, извлекая квадратный корень на листке бумаги.

Системы линейных алгебраических уравнений возникают как промежуточный или окончательный этап при решении ряда прикладных задач, описываемых дифференциальными, интегральными или системами нелинейных (трансцендентных) уравнений. Они могут появляться как этап в задачах математического программирования, статистической обработки данных, аппроксимации функций, при дискретизации краевых дифференциальных задач методом конечных разностей, методом конечных элементов, проекционными методами, в методе граничных элементов, дискретных особенностей, панельном методе аэродинамической компоновки летательного аппарата и т.д.

Матрицы возникающих систем могут иметь различные структуры и свойства. Уже сейчас имеется потребность в решении систем линейных алгебраических уравнений с матрицами полного заполнения порядка нескольких тысяч. При решении ряда прикладных задач методом конечных элементов в ряде случаев появляются системы, обладающие симметричными положительно определёнными ленточными матрицами порядка несколько десятков тысяч с половиной ширины ленты до тысячи. И, наконец, при использовании в ряде задач метода конечных разностей необходимо решить системы разностных уравнений с разрежёнными матрицами порядка миллион.

Одним из самых распространенных методов решения систем линейных уравнений является метод вращений Якоби. Этот метод (который также называют методом простых итераций) известен в различных вариантах уже более 200 лет.

2. Основные определения

2.1 Определения собственного значения и собственного и вектора матрицы

Рассмотрим квадратную матрицу n-ого порядка:

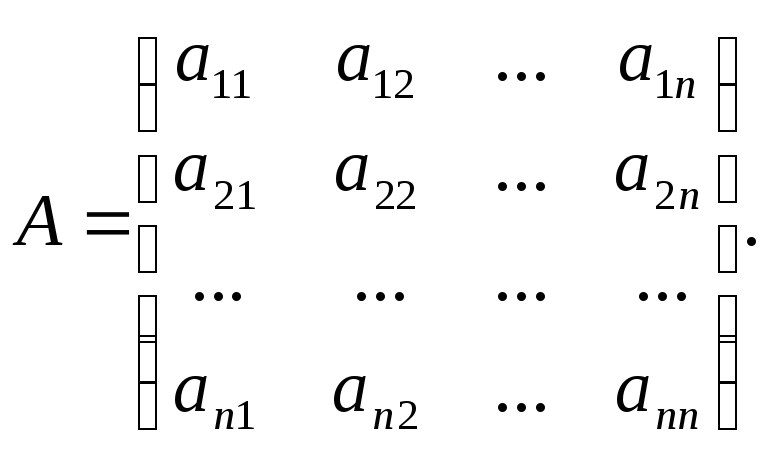
Собственные значения _i квадратной матрицы A есть действительные или комплексные числа, удовлетворяющие условию:

,

E – единичная матрица,

- собственный вектор матрицы A, соответствующий некоторому собственному значению .

Матрица называется характеристической матрицей матрицы A. Т.к. в матрице по главной диагонали стоят , а все остальные элементы равны нулю, то характеристическая матрица имеет вид:

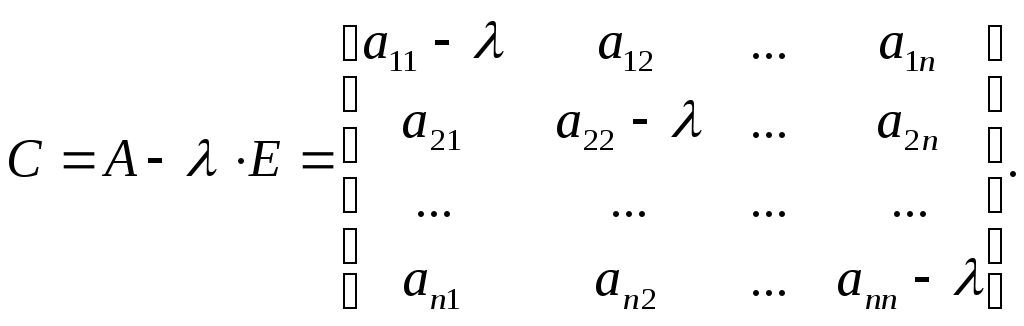
Определитель этой матрицы называется характеристическим определителем и равен:

В развернутом виде он является многочленом n-ой степени относительно , т.к. при вычислении этого определителя произведение элементов главной диагонали дает многочлен со старшим членом , т.е.

и называется характеристическим многочленом. Корни этого многочлена – собственные значения или характеристические числа матрицы A. Числа называются коэффициентами характеристического многочлена.

Ненулевой вектор называется собственным вектором матрицы A, если эта матрица переводит вектор X в вектор

,

т.е. произведение матрицы A на вектор X и произведение характеристического числа  на вектор X есть один и тот же вектор. Каждому собственному значению матрицы соответствует свой собственный вектор .

Для определения координат собственного вектора составляется характеристическое уравнение: . Переписав его в векторном виде и выполнив умножение, получим систему линейных однородных уравнений:

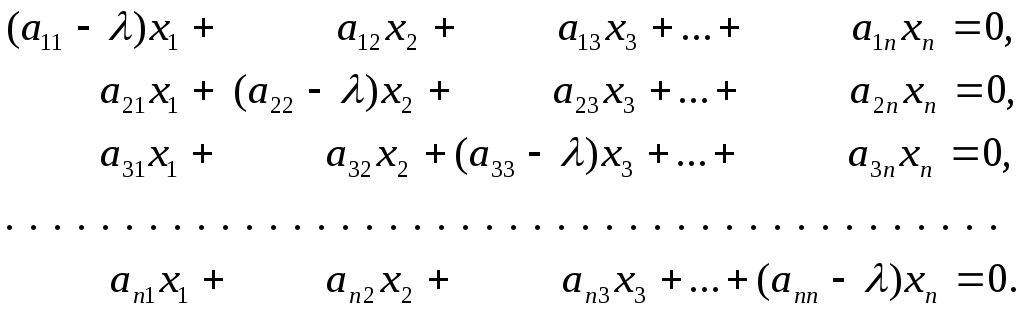
Определитель этой системы равен нулю, т.к. из этого условия были определены собственные значения матрицы A. Следовательно, система имеет бесконечное множество решений. Ее можно решить с точностью до постоянного множителя (как систему однородных уравнений). Решив эту систему, мы найдем все координаты собственного вектора X. Подставляя в систему однородных уравнений поочередно , получаем n собственных векторов.

При определении собственных значений и принадлежащих им собственных векторов решается одна и двух задач:

1. Определение все собственных значений и принадлежащих им собственных векторов матриц;

2. Определение одного или нескольких собственных значений и принадлежащих им собственных векторов.

Первая задача состоит в развертывании характеристического определителя в многочлен n-й степени (т.е. в определении коэффициентов ) с последующим вычислением собственных значений и, наконец, в определении координат собственного вектора .

Вторая задача заключается в определении собственных значений итерационными методами без предварительного развертывания характеристического определителя (метод итераций). Методы первой задачи (метод Данилевского, метод Леверрье-Фаддеева) относятся к точным, т.е. если их применить для матриц, элементы которых заданы точно (рациональными числами), и точно проводить вычисления (по правилам действий с обыкновенными дробями), то в результате будет получено точное значение коэффициентов характеристического многочлена, и координаты собственных векторов окажутся выраженными точными формулами через собственные значения.

Обычно собственные векторы матрицы удается определить, используя промежуточные результаты вычислений, проведенных для определения коэффициентов характеристического многочлена. Для определения того или иного собственного вектора, принадлежащего собственному значению, это собственное значение должно быть уже вычислено.

Методы решения второй задачи – итерационные. Здесь собственные значения получаются как пределы некоторых числовых последовательностей, так же, как и координаты принадлежащих им собственных векторов. Т.к. эти методы не требуют вычисления коэффициентов характеристического многочлена, то он менее трудоемки.

Пример нахождения собственных значений и собственных векторов матрицы

Найти собственные значения и собственные векторы матрицы

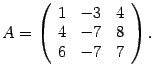
Решение. Составляем характеристическую матрицу :

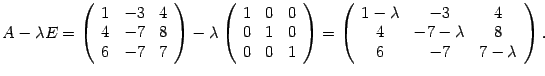
Находим характеристический многочлен

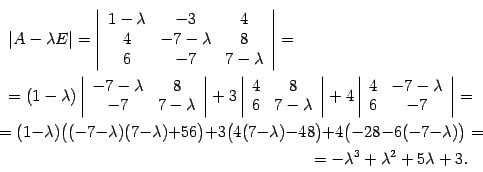
Решим характеристическое уравнение

Подбором находим, что один корень уравнения равен -1. Есть теорема, которая говорит, что если число c является корнем многочлена , то многочлен делится на разность , то есть , где  -- многочлен. В соответствии с этой теоремой многочлен должен делиться на . Выделим в характеристическом многочлене этот множитель :

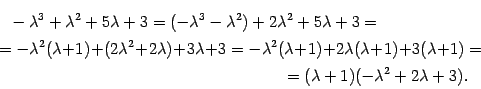
Находим корни трехчлена . Они равны -1 и 3. Таким образом,

 -- корень кратности 2 ,  -- простой корень. Итак, собственные числа матрицы A равны , . Найдем соответствующие им собственные векторы.

Пусть , тогда для собственного вектора получаем матричное уравнение

что соответствует системе уравнений

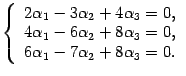
Решаем ее методом Гаусса. Выписываем расширенную матрицу системы

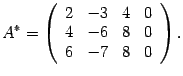
Первую строку, умноженную на числа -2 и -3 прибавляем соответственно ко второй и третьей строкам

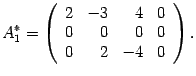
Меняем местами вторую и третью строки

Возвращаемся к системе уравнений

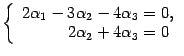
Базисный минор матрицы находится в первых двух столбцах и первых двух строках, ранг равен 2. Поэтому фундаментальная система содержит только одно решение. Переменные и оставляем в левой части, а переменное переносим в правую часть

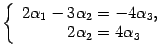
Полагаем , находим , . Итак, собственному числу соответствует собственный вектор .

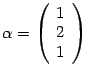Пусть , тогда для собственного вектора получаем матричное уравнение

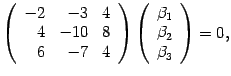
что соответствует системе уравнений

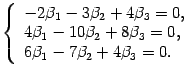
Решаем ее методом Гаусса. Выписываем расширенную матрицу

Первую строку умножаем на числа 2 и 3 и прибавляем соответственно ко второй и третьей строкам

Вторую строку умножаем на -1 и прибавляем к третьей

Возвращаемся к системе уравнений

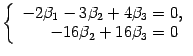
Базисный минор матрицы находится в первых двух столбцах и первых двух строках, ранг равен 2. Поэтому фундаментальная система содержит только одно решение. Переменные и оставляем в левой части, а переменное переносим в правую часть

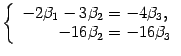
Полагаем , находим , . Итак, собственному числу соответствует собственный вектор 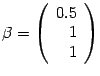. Чтобы избавиться от дроби, умножим собственный вектор на 2, получим собственный вектор с тем же самым собственным числом. В итоге собственному числу соответствует собственный вектор .

Ответ: Собственные числа: , , соответствующие собственные векторы: , .
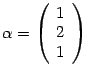
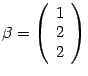