§3. Формула Тейлора

Если функция в некоторой окрестности точки имеет производную, то для любого из этой окрестности справедлива формула Тейлора

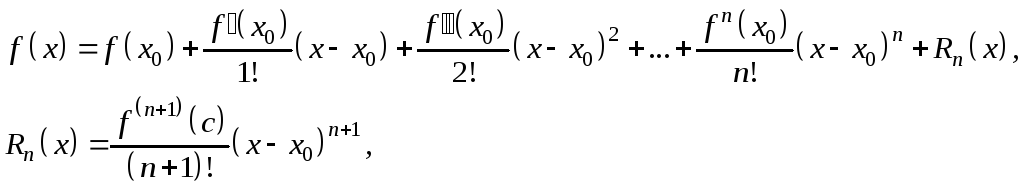
или

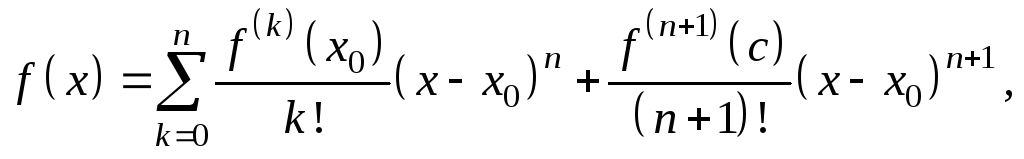
где (по определению). Точка расположена между и . В данном случае остаточный член записан в форме Лагранжа.

Полагая в формуле Тейлора , получим формулу Маклорена.

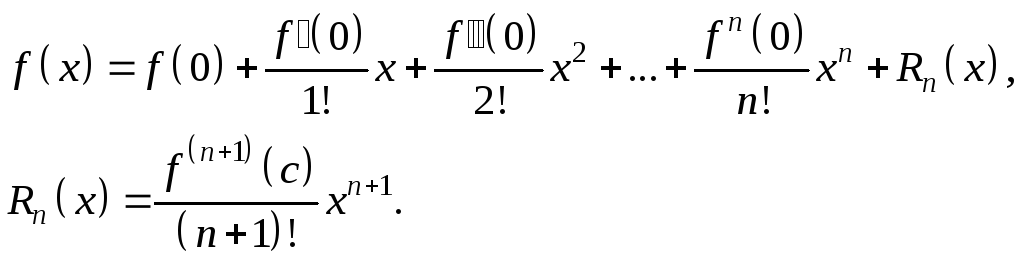
Пример 7. Многочлен разложить по степеням .

Решение. Так как данный многочлен имеет степень 3, то все производные порядка выше 3 будут тождественно равны нулю. В данном случае .

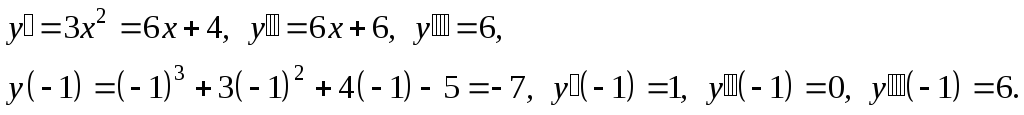
По формуле Тейлора имеем:

.

Написать формулу Маклорена при для функций

Написать формулу Тейлора при для функций

.

Формула Тейлора (в частности Маклорена) часто используется в приближённых вычислениях.

или

.

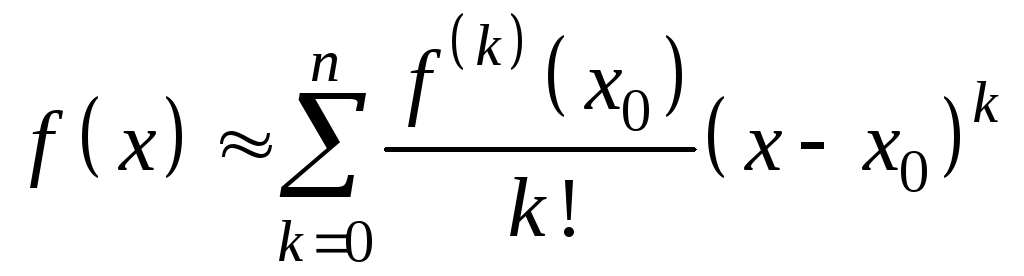При этом ошибка равна 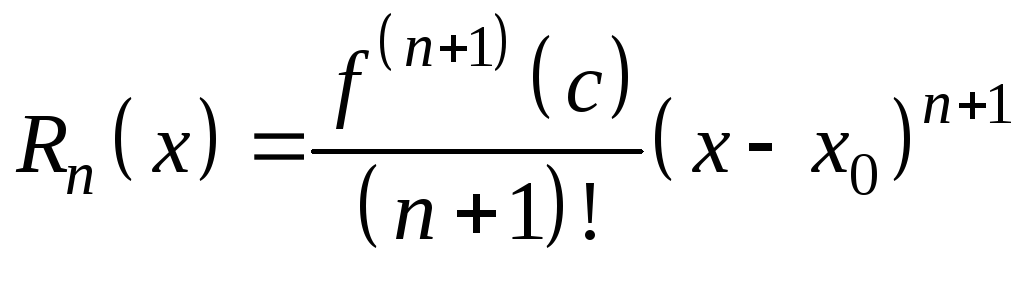, где точка расположена между и .

Пример 8. Вычислить с точностью .

Решение. Рассмотрим функцию , которая бесконечное число раз дифференцируема на всей числовой оси, при этом . Поэтому для функции можно написать формулу Маклорена при любом .

,

где 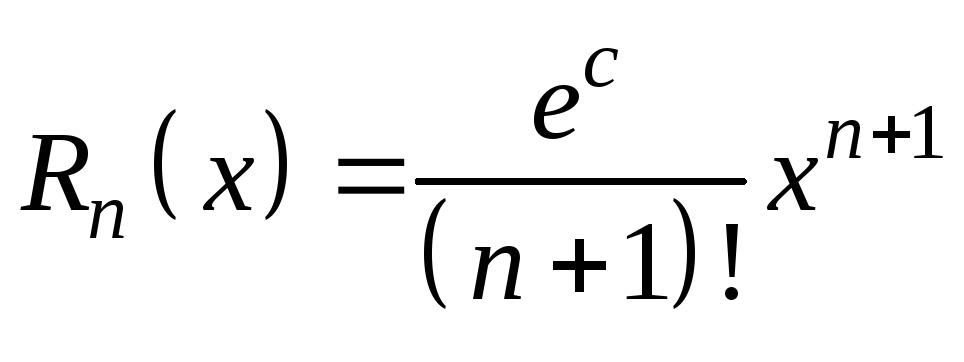, точка расположена между 0 и .

При будем иметь:

, где

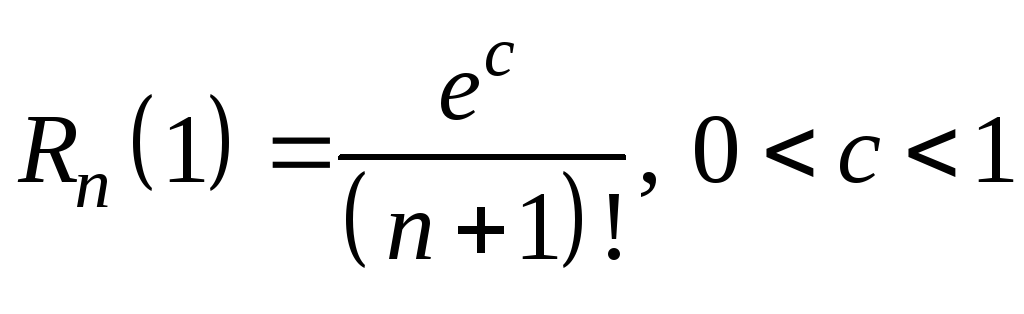
Отсюда имеем:

, при этом ошибка равна .

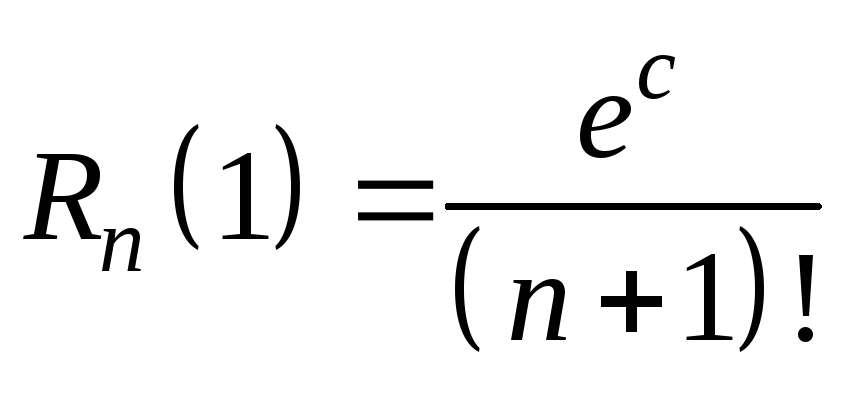Оценим остаток, учитывая неравенство , 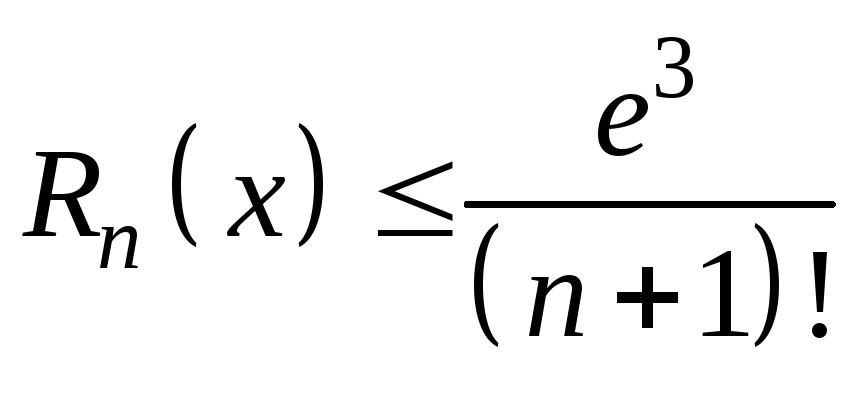. Подберём наименьшее , чтобы выполнялось неравенство . Легко видеть, что , т.к. . Следовательно, .

Вычислить с точностью до следующие значения

30. а) б) в) г)

§4. Исследование функций и построение графиков

4.1. Возрастание и убывание функций. Экстремумы

Определение 1. Функция называется возрастающей (убывающей) в интервале , если , следует неравенство ().

Теорема 1. Если и обращается в нуль в точках, которые не заполняют полностью никакого отрезка внутри , то возрастает (убывает) в интервале .

Пример 9. Найти промежутки возрастания и убывания функции .

Решение. Данная функция определена и дифференцируема на всей числовой оси. . Так как , то на всей числовой оси; только в тех точках, где , т.е. в точках . Производная данной функции обращается в нуль в бесконечном числе точек, но эти точки не заполняют полностью никакого промежутка. Поэтому данная функция возрастает на всей числовой оси.

Пример 10. Найти промежутки возрастания и убывания функции .

Решение. Данная функция определена и дифференцируема на всей числовой оси. . При , а при . Следовательно, в интервале данная функция возрастает, а в интервале убывает.

Определение 3. Функция в точке имеет экстремум, если в этой точке функция имеет максимум или минимум.

Необходимое условие экстремума.

Теорема 2. Если функция в точке имеет экстремум, то в этой точке производная равна нулю или не существует.

Это необходимое условие не является достаточным, т.е. производная в точке может быть равна нулю или не существует, а экстремума в этой точке функция может не иметь.

Пример 11. , но в точке данная функция не имеет ни максимума, ни минимума.

П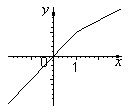ример 12.

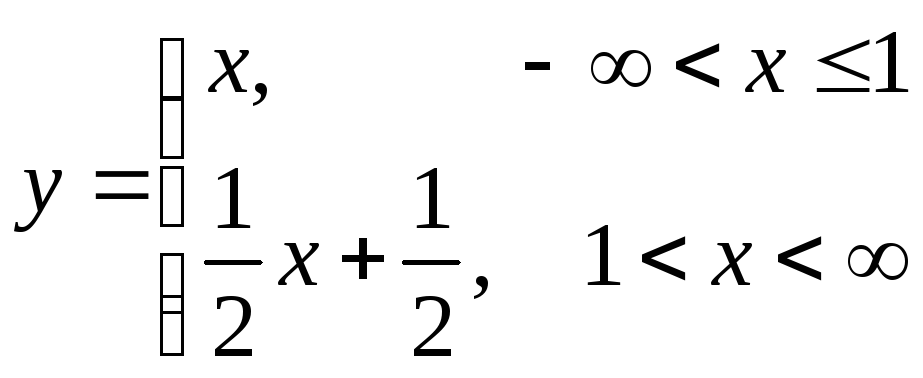
Производная данной функции слева в точке равна 1, т.е. , справа в точке равна , т.е. . Следовательно, производная от данной функции в точке не существует. Легко видеть, что данная функция в точке экстремума не имеет, т.к. она на всей числовой оси возрастает.

Определение 4. Точка , в которой первая производная равна нулю или не существует, называется критической точкой.

Определение 5. Если , то точка называется стационарной.

Теорема 4. Если в стационарной точке существует вторая производная и , то в точке функция имеет максимум. Если , то в точке функция имеет минимум. Если , то требуются дополнительные исследования.

Пример 13. Найти точки экстремума функции .

Решение. Функция определена на всей числовой оси. Найдём критические точки.

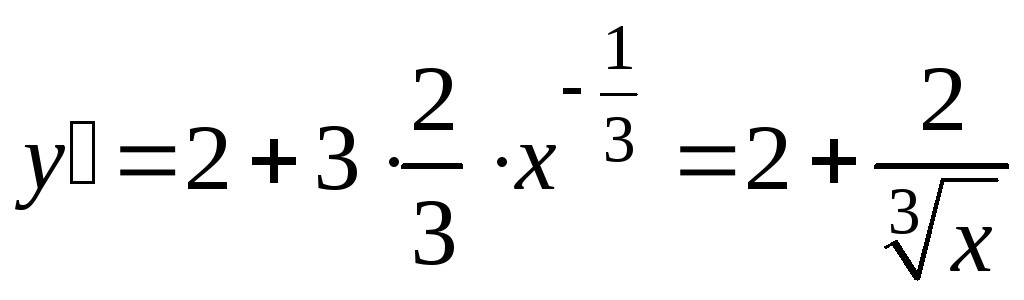
1. В точке 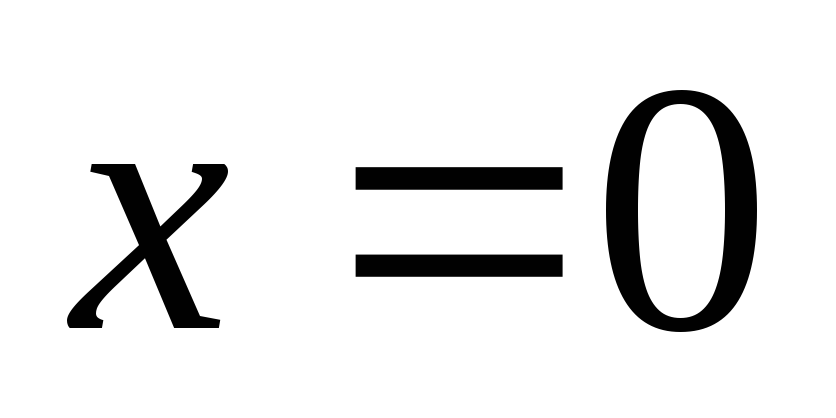производная не существует.

2. .

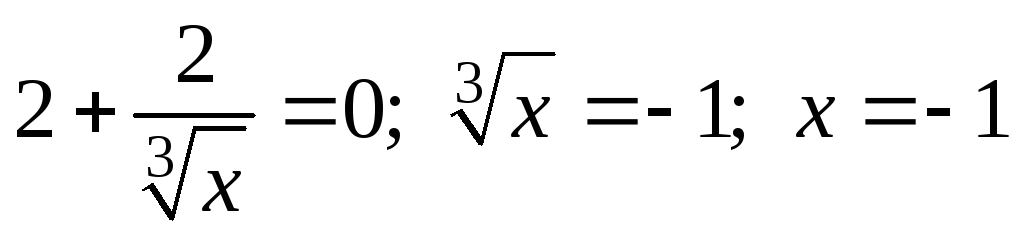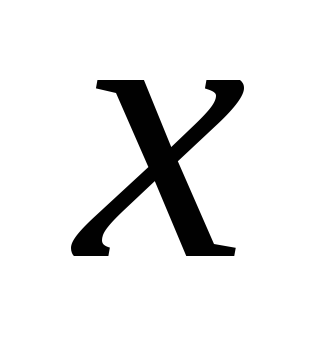
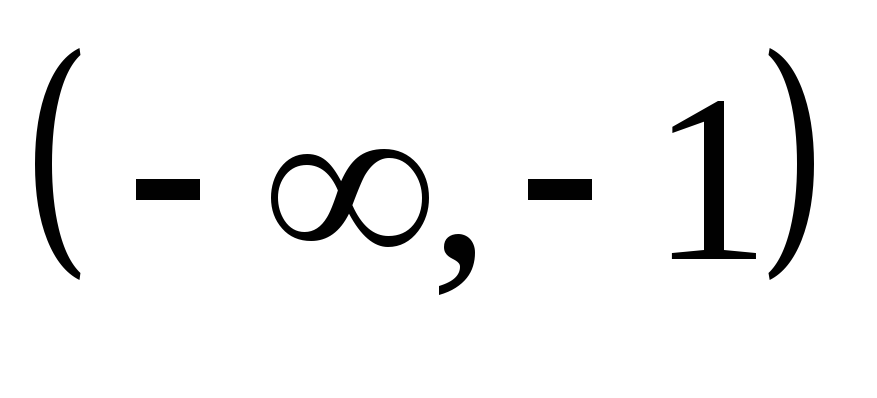
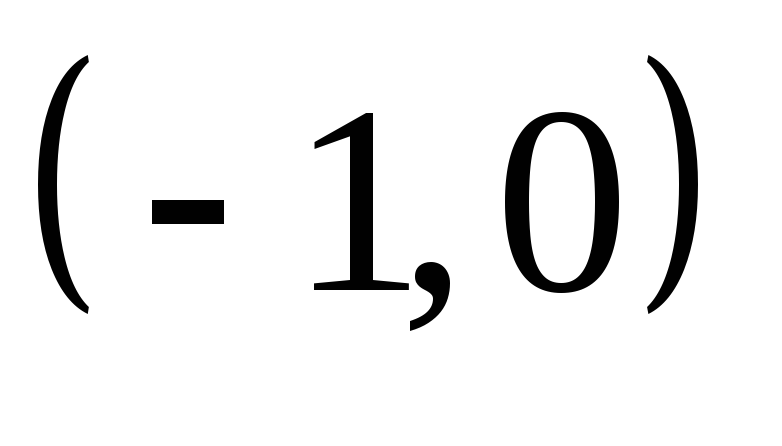
				0
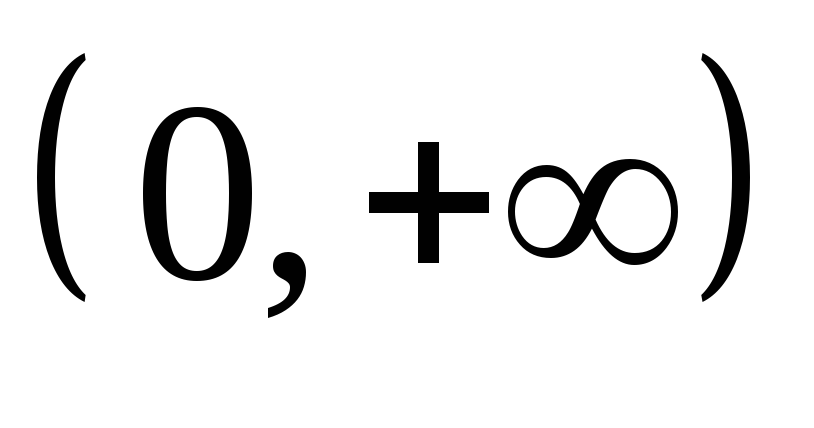
	+	0		не сущ.	+
		1 max		0 min

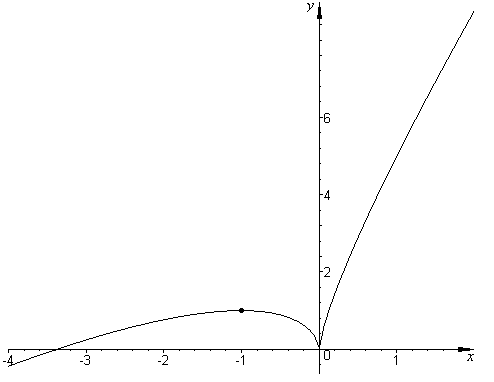
Рис.1

Итак, функция в точке имеет максимум равный 1, а в точке имеет минимум равный 0.

Найти промежутки возрастания и убывания функции, экстремумы функции.

31.	34.	37.
32.	35.
33.	36.