- •Введение
- •§1. Теоремы Ролля, Лагранжа, Коши
- •§2. Теоремы Лопиталя-Бернулли
- •§3. Формула Тейлора
- •§4. Исследование функций и построение графиков
- •4.1. Возрастание и убывание функций. Экстремумы
- •4.2. Нахождение наименьшего и наибольшего значений непрерывной функции на отрезке
- •4.3. Нахождение промежутков выпуклости и вогнутости графика функции, точек перегиба
- •4.4. Нахождение асимптот графика функции
- •4.5. Полное исследование функций и построение графиков
- •Использованная литература
Оглавление
Введение 3
§1. Теоремы Ролля, Лагранжа, Коши 3
§2. Теоремы Лопиталя-Бернулли 5
§3. Формула Тейлора 8
§4. Исследование функций и построение графиков 11
4.1. Возрастание и убывание функций. Экстремумы 11
4.2. Нахождение наименьшего и наибольшего значений непрерывной функции на отрезке 14
4.3. Нахождение промежутков выпуклости и вогнутости графика функции, точек перегиба 15
4.4. Нахождение асимптот графика функции 16
4.5. Полное исследование функций и построение графиков 18
Использованная литература 22
Применение производной
Введение
Производная находит широкое применение при решении различных задач. В настоящей методической работе приведен необходимый материал без доказательства, который проиллюстрирован примерами. Далее приведены примеры для самостоятельного решения. Нами рассмотрены теоремы Ролля, Лагранжа, Коши. Теоремы Лопиталя-Бернули для раскрытия неопределенностей при вычислении пределов, формула Тейлора и применение производной для исследования функций.
Для понимания материала и решения задач студенту необходимо знать таблицу производных и правила дифференцирования функций. Методическая работа может быть использована студентами и преподавателями на практических занятиях по данной теме.
§1. Теоремы Ролля, Лагранжа, Коши
Теорема Ролля. Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
дифференцируема в интервале
,
дифференцируема в интервале
![]() и на концах отрезка принимает равные
значения, т.е.
и на концах отрезка принимает равные
значения, т.е.
![]() ,
то существует точка
,
то существует точка
![]() такая, что
такая, что
![]() .
Точки, в которых
.
Точки, в которых
![]() ,
называются стационарными точками
функции
,
называются стационарными точками
функции
![]() .
.
Теорема Лагранжа. Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
дифференцируема в интервале
,
дифференцируема в интервале
![]() ,
то существует точка
,
то существует точка
![]() такая, что справедливо равенство
такая, что справедливо равенство
![]() .
.
Теорема
Коши. Если функции
![]() и
и
![]() непрерывны на отрезке
непрерывны на отрезке
![]() ,
дифференцируемы в интервале
,
дифференцируемы в интервале
![]() и
и
![]() ,
то существует точка
,
то существует точка
![]() такая, что
такая, что
![]() .
.
Решить следующие задачи:
-
Функция
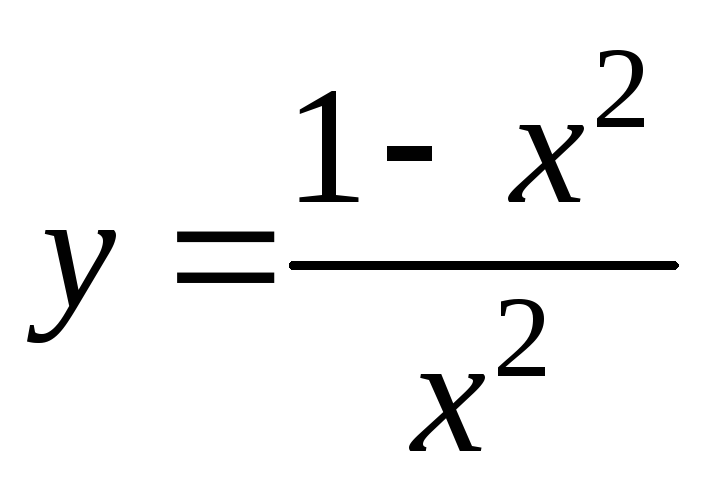 имеет на концах отрезка
имеет на концах отрезка
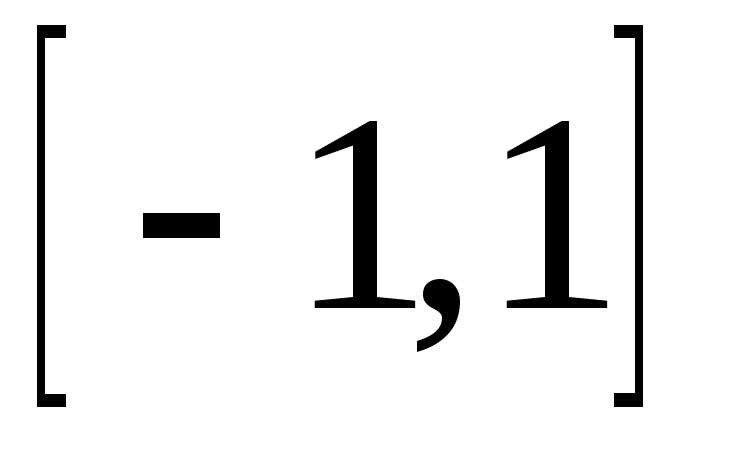 равные значения (проверьте). Производная
данной функции в интервале
равные значения (проверьте). Производная
данной функции в интервале
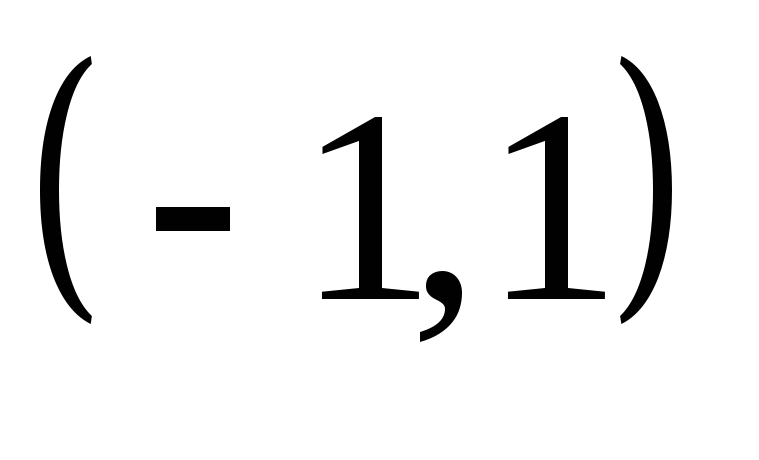 не обращается в нуль ни в одной точке
(проверьте). Какие условия Теоремы Ролля
для данной функции на отрезке
не обращается в нуль ни в одной точке
(проверьте). Какие условия Теоремы Ролля
для данной функции на отрезке
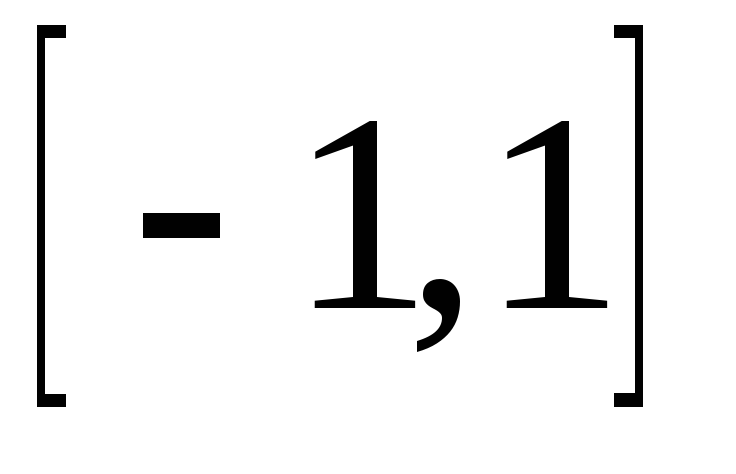 не выполнены?
не выполнены? -
Пусть
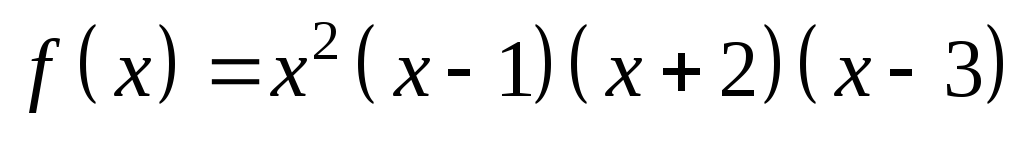 .
Показать, что три корня уравнения
.
Показать, что три корня уравнения
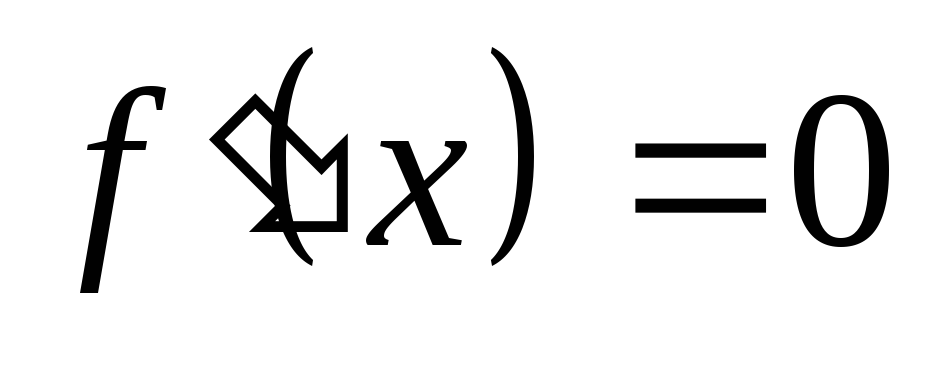 действительны.
действительны. -
Доказать, что уравнение
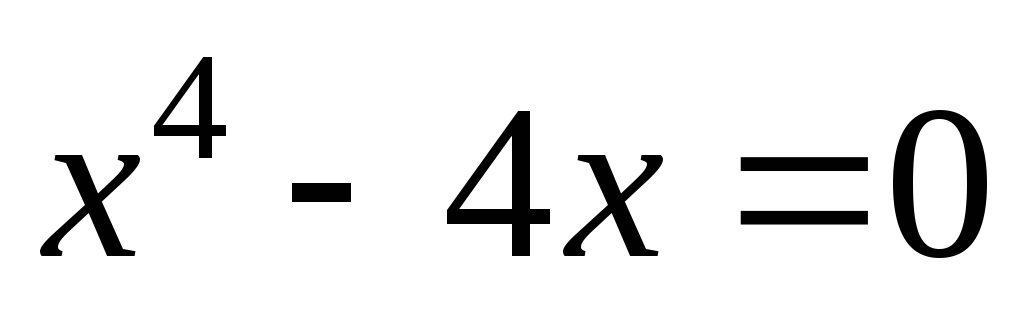 не имеет корней в интервале
не имеет корней в интервале
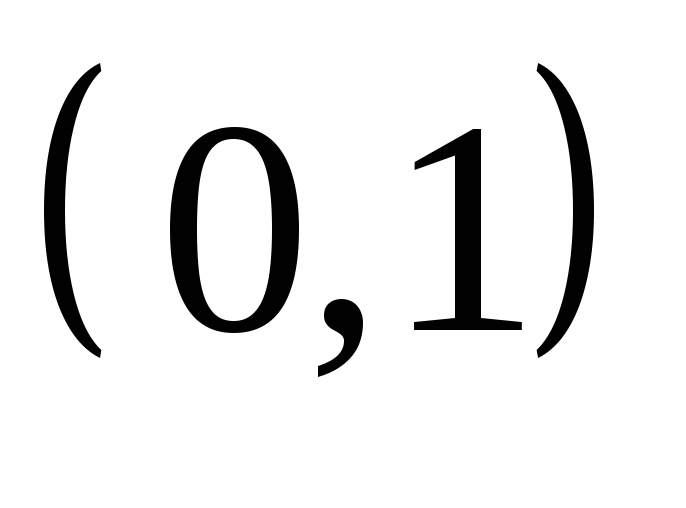 .
. -
Пусть
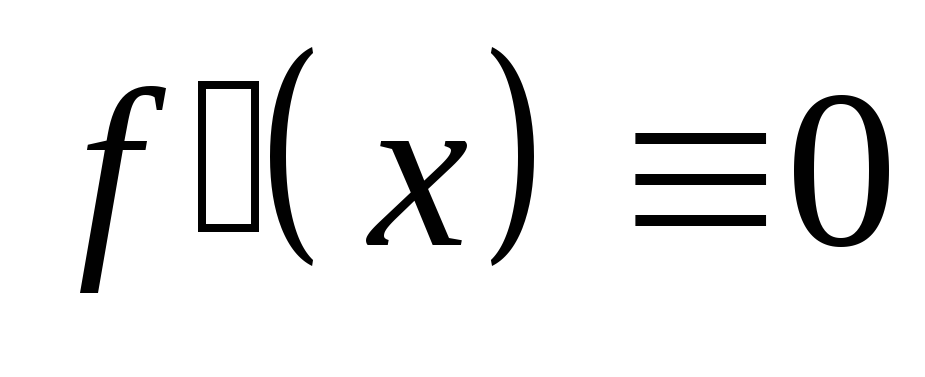 в интервале
в интервале
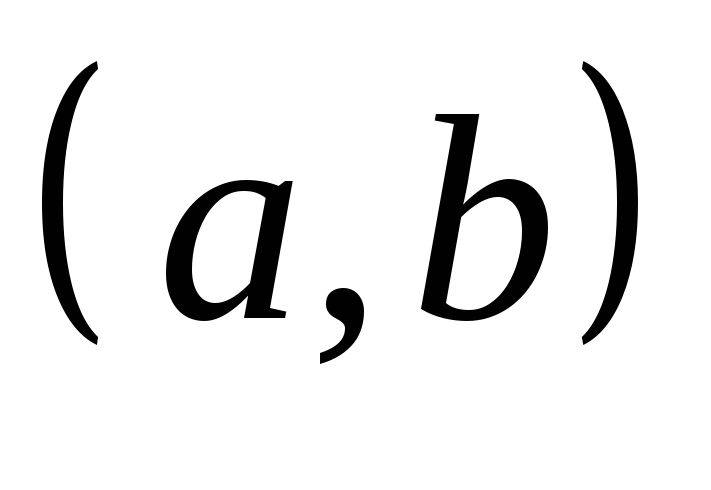 .
Доказать, что
.
Доказать, что
 на
на
 .
. -
Пусть
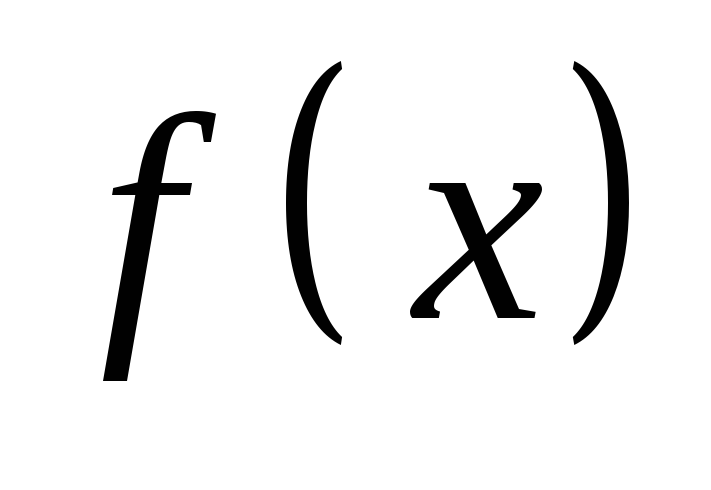 и
и
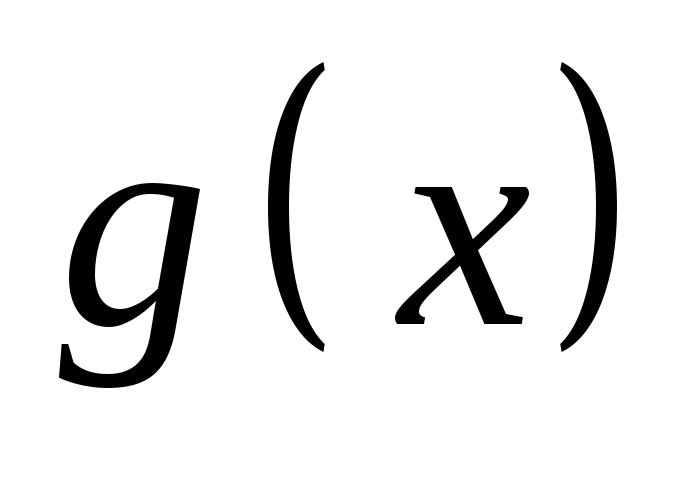 удовлетворяют всем условиям Теоремы
Коши на
удовлетворяют всем условиям Теоремы
Коши на
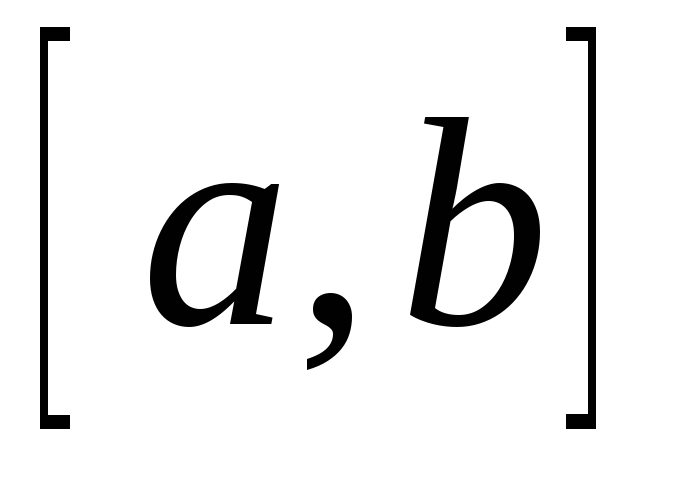 .
Применим Теорему Лагранжа к функциям
.
Применим Теорему Лагранжа к функциям
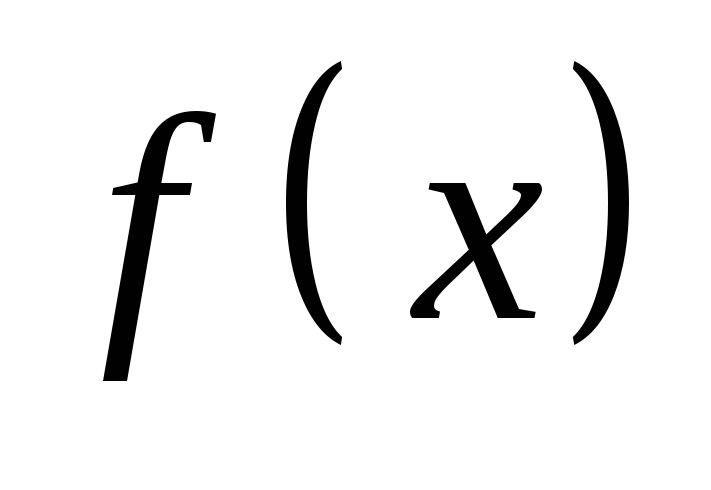 и
и
 ,
тогда получим
,
тогда получим
 .
Из последних двух равенств получим:
.
Из последних двух равенств получим:
![]() (Формула Коши)
(Формула Коши)
Найти ошибку в доказательстве.
§2. Теоремы Лопиталя-Бернулли
Раскрытие
неопределённостей типа
![]() и
и
![]()
Первая теорема Лопиталя-Бернулли. Пусть
для функций
![]() и
и
![]() выполнены условия:
выполнены условия:
-
Функции
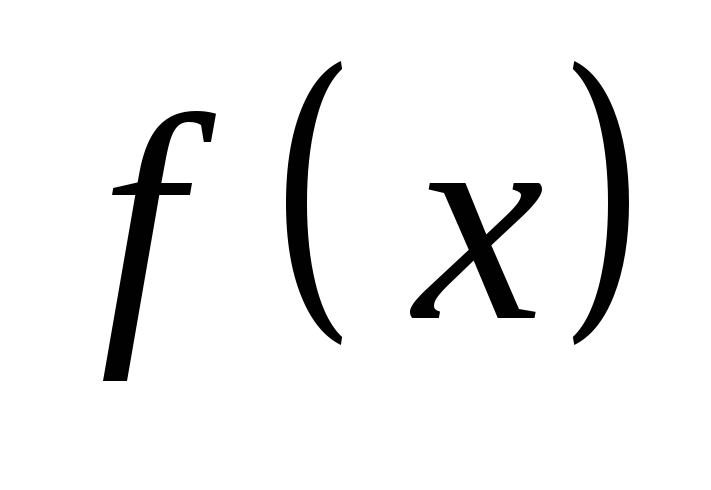 и
и
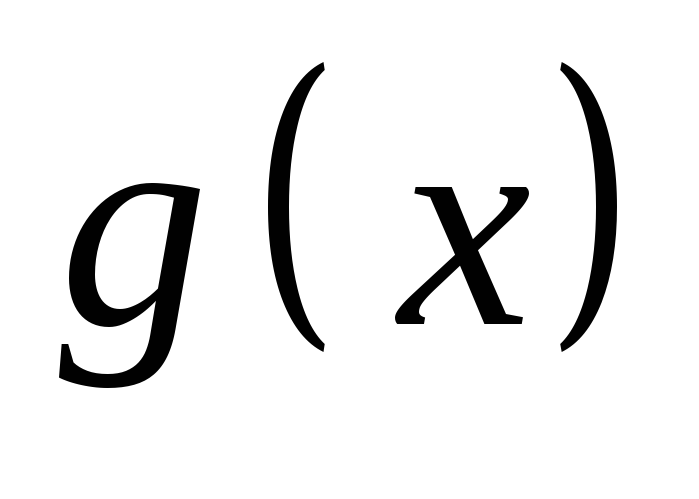 дифференцируемы в промежутке
дифференцируемы в промежутке
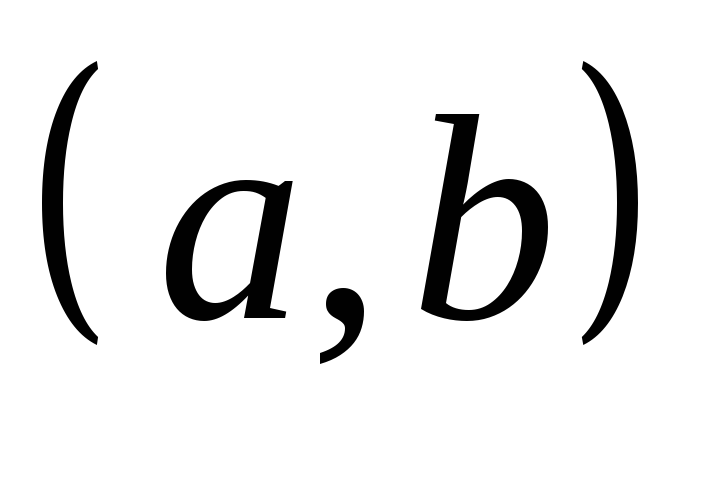 и
и
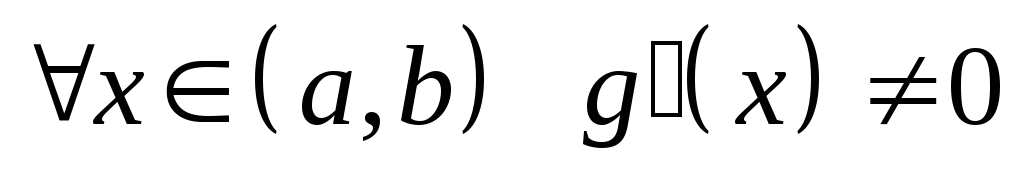
-
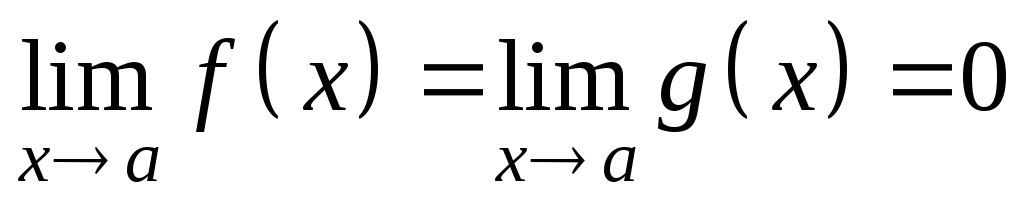
-
Существует предел
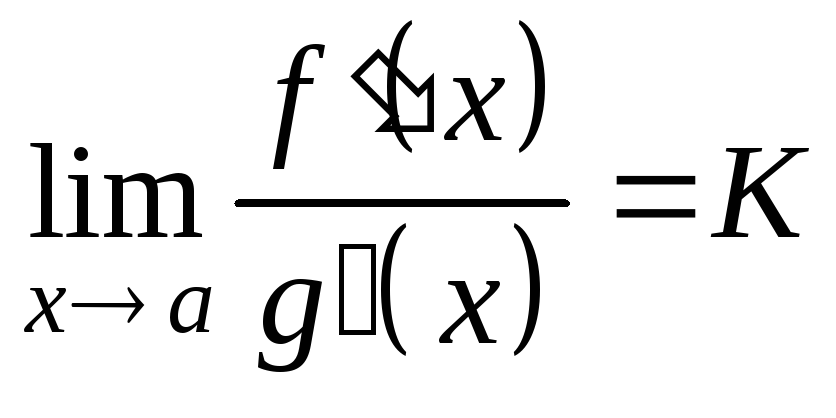 .
Тогда
.
Тогда
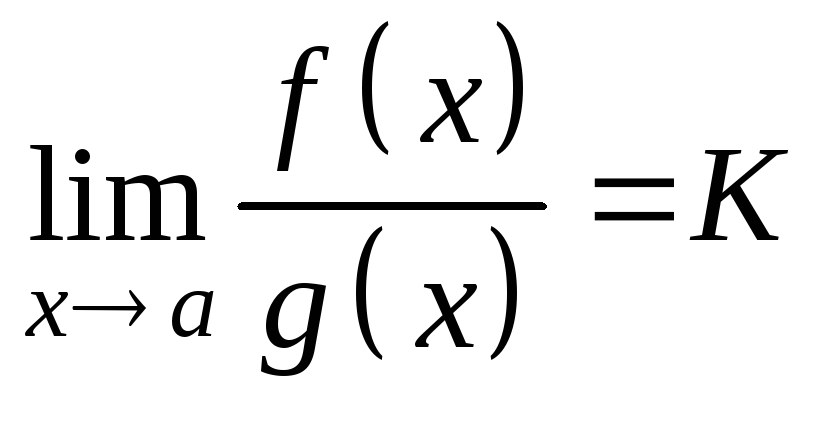
Вторая теорема Лопиталя-Бернулли. Пусть
для функций
![]() и
и
![]() выполнены условия:
выполнены условия:
-
Функции
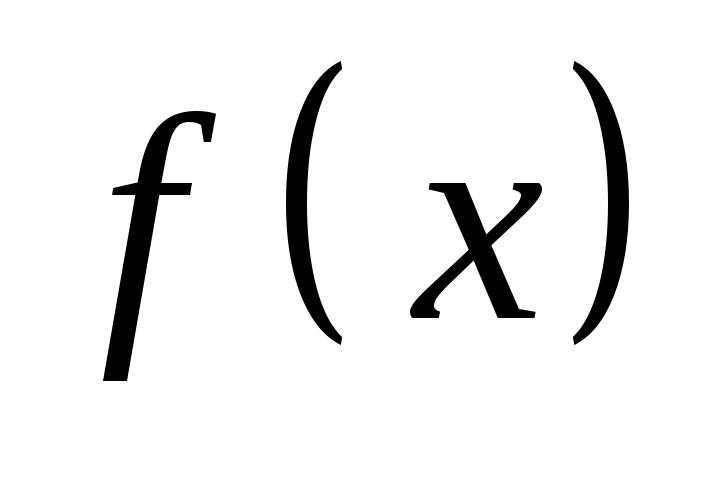 и
и
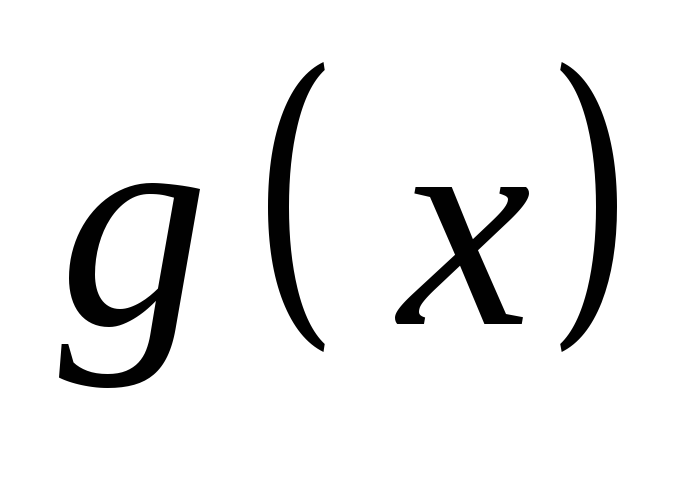 дифференцируемы в промежутке
дифференцируемы в промежутке
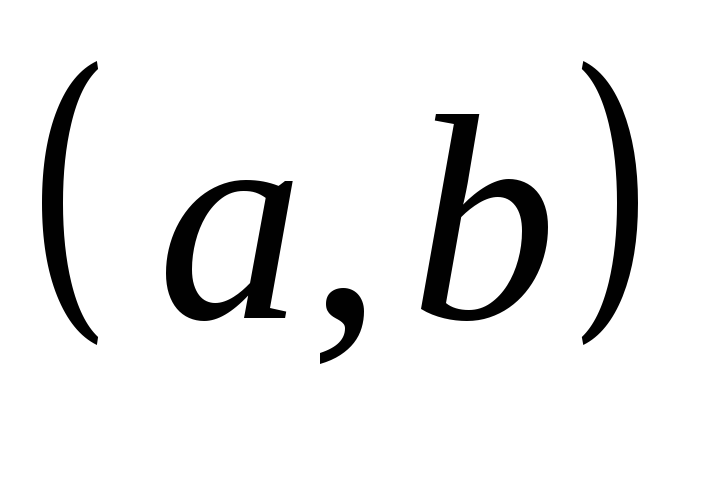 ,
причем
,
причем
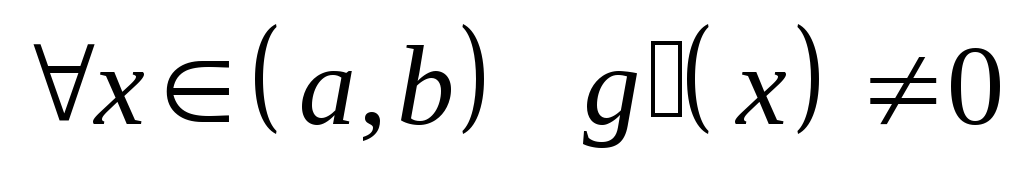
-
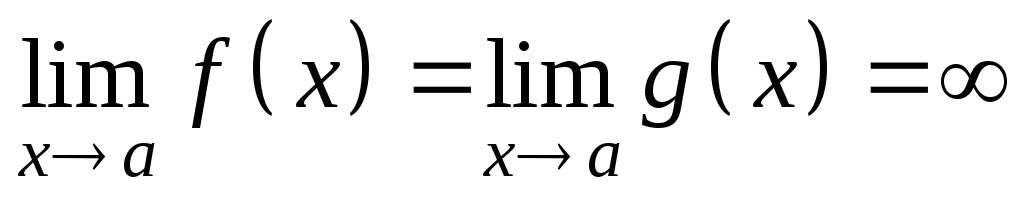
-
Существует предел
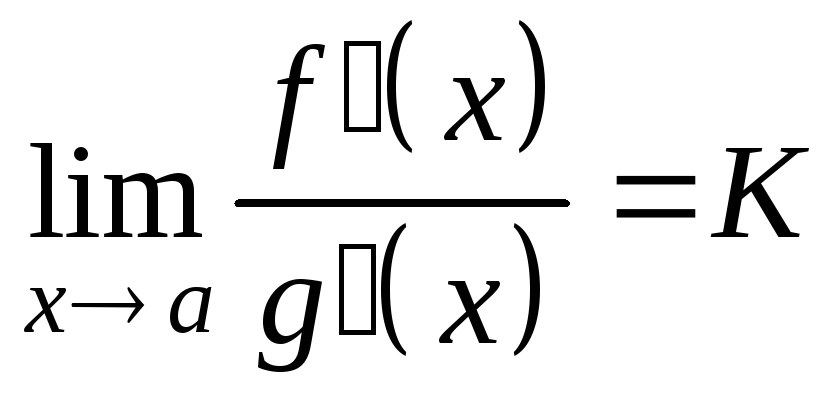 .
Тогда
.
Тогда
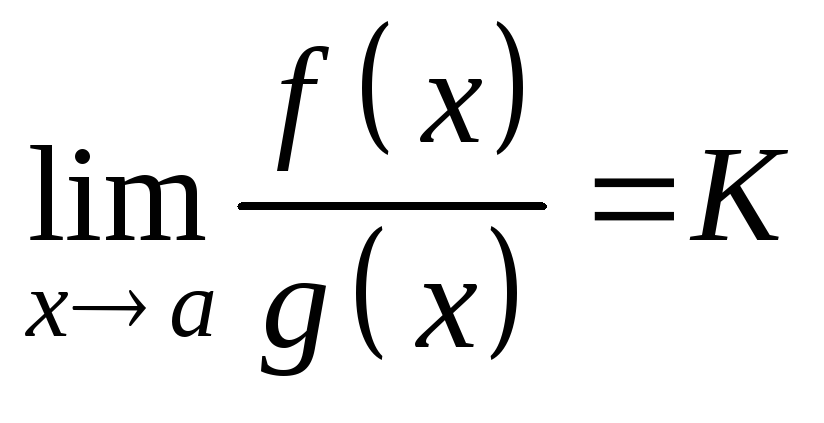
Замечание. Теоремы Лопиталя-Бернулли
справедливы и при
![]() .
.
Пример 1. Вычислить предел
![]() .
.
Решение.
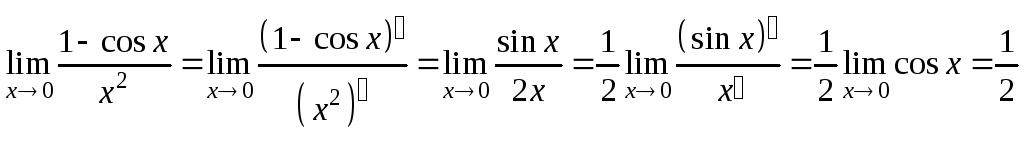
Пример 2. Вычислить предел
![]() .
.
Решение.

Этот пример показывает, что степенная
функция
![]() даже с очень большим показателем при
даже с очень большим показателем при
![]() растет медленнее, чем показательная
функция.
растет медленнее, чем показательная
функция.
Раскрытие
неопределённостей типа
![]()
Неопределённость
типа
![]() возникает при нахождении пределов от
произведения двух функций, т.е.
возникает при нахождении пределов от
произведения двух функций, т.е.
![]() ,
где
,
где
![]() ,
а
,
а
![]() .
В этом случае произведение
.
В этом случае произведение
![]() записывают так, чтобы можно было
воспользоваться первой или второй
теоремой Лопиталя-Бернулли.
записывают так, чтобы можно было
воспользоваться первой или второй
теоремой Лопиталя-Бернулли.
Пример
3. Вычислить предел
![]() .
.
Решение.
В данном примере неопределённость
![]() ,
которую сведём к неопределённости
,
которую сведём к неопределённости
![]() и применим вторую теорему Лопиталя-Бернулли.
и применим вторую теорему Лопиталя-Бернулли.
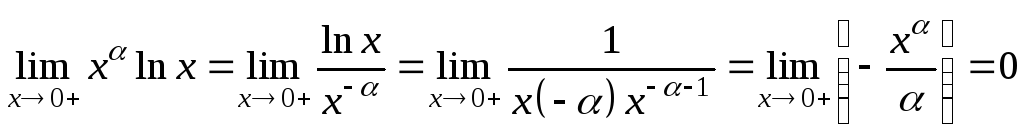 .
.
Пример
4. Вычислить предел
![]() .
.
Решение.
Имеем неопределённость
![]() .
.
![]() .
.
Мы
воспользовались соотношением
![]() при
при
![]() .
Применяя далее первую теорему
Лопиталя-Бернулли, получим:
.
Применяя далее первую теорему
Лопиталя-Бернулли, получим:

Неопределённости
вида
![]() возникают при вычислении пределов
возникают при вычислении пределов
![]() .
Для вычисления данного предела
предварительно вычисляют предел
.
Для вычисления данного предела
предварительно вычисляют предел
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() .
.
Таким
образом, раскрытие неопределенностей
![]() сводится к раскрытию соответственно
неопределённостей
сводится к раскрытию соответственно
неопределённостей
![]() ,
которые в свою очередь могут быть сведены
к раскрытию неопределённостей
,
которые в свою очередь могут быть сведены
к раскрытию неопределённостей
![]() или
или
![]() с применением соответствующих теорем
Лопиталя-Бернулли.
с применением соответствующих теорем
Лопиталя-Бернулли.
Пример
5. Вычислить предел
![]() .
.
Решение.
Имеем неопределённость
![]() .
Предварительно вычислим предел
.
Предварительно вычислим предел
![]() .
В данном случае мы использовали
соотношение
.
В данном случае мы использовали
соотношение
![]() ,
и результат примера 3.
,
и результат примера 3.
Пример
6. Вычислить предел
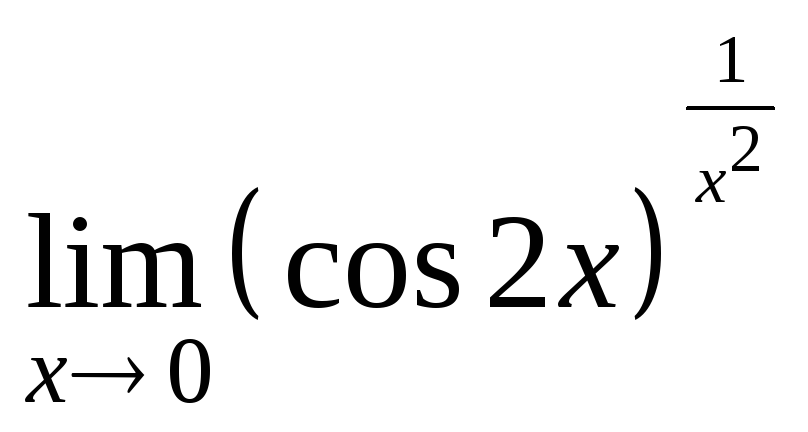 .
.
Решение.
Имеем неопределённость
![]() .
Логарифмируя и применяя теорему
Лопиталя-Бернулли, получим:
.
Логарифмируя и применяя теорему
Лопиталя-Бернулли, получим:
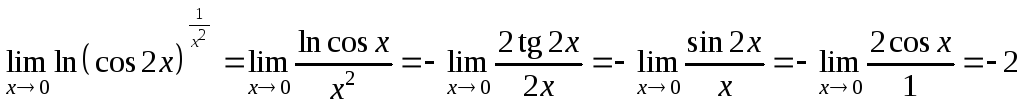 .
.
Отсюда
имеем:
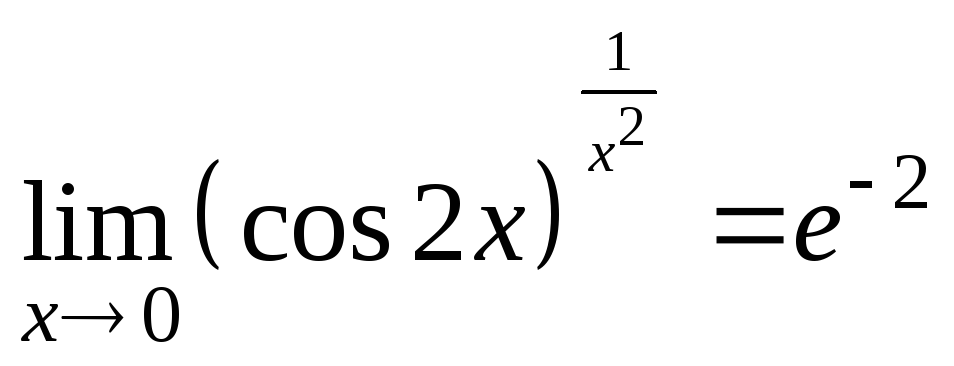 .
.
Найти следующие пределы
|
6.
|
14.
|
22.
|
|
7.
|
15.
|
23.
|
|
8.
|
16.
|
24.
|
|
9.
|
17.
|
25.
|
|
10.
|
18.
|
26.
|
|
11.
|
19.
|
27.
|
|
12.
|
20.
|
28.
|
|
13.
|
21.
|
29.
|