Метод вариации произвольных постоянных
Рассмотрим
общий метод нахождения частных решений
неоднородного уравнения как с постоянными,
так и с переменными коэффициентами и с
произвольной правой частью f(x),
называемый методом вариации произвольных
постоянных. Метод заключается в следующем.
Пусть известно общее решение
соответствующего однородного уравнения
Тогда решение неоднородного уравнения
ищется в виде
,
где постоянные
и
заменены некоторыми функциями
и
которые подбираются так, чтобы y
было решением неоднородного уравнения.
Дифференцируя y,
получим
Так
как неизвестных функций две, а уравнение
одно, введем дополнительное условие:
выберем неизвестные функции так, чтобы
выполнялось условие
.
Тогда
.
Дифференцируя последнее равенство еще
раз, получим
Подставляя выражения для
и
в уравнение, получим
или,
группируя слагаемые,
(*)
Так
как
- решение однородного уравнения, то
то есть выражение в первой скобке
обращается в нуль. Аналогично выражение
во второй скобке равно нулю, так как
также является решением однородного
уравнения.
Таким
образом, равенство (*) принимает вид
.
Объединяя
уравнения
и
,
получаем систему уравнений относительно
неизвестных
и
.
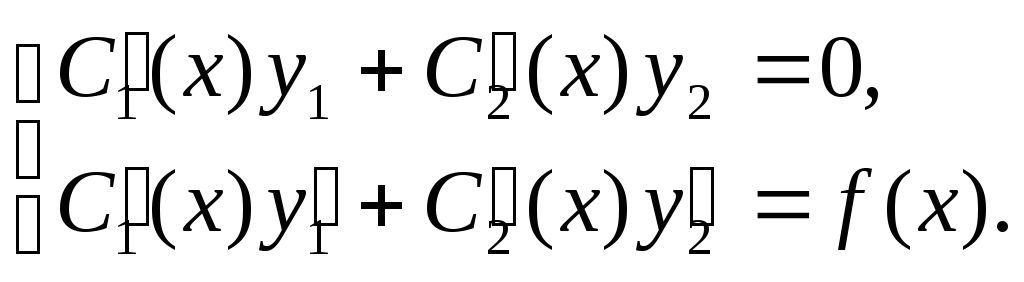
Решив
эту систему, находим
и
,
а затем, интегрируя эти функции и
подставляя в
,
получим общее решение данного неоднородного
уравнения.
Пример
19. Найти
общее решение уравнения
.
Решение.
В примере 9 было найдено общее решение
соответствующего однородного уравнения
в виде
Значит, общее решение неоднородного уравнения будем искать в виде
Составим
систему уравнений для нахождения функций
и
:
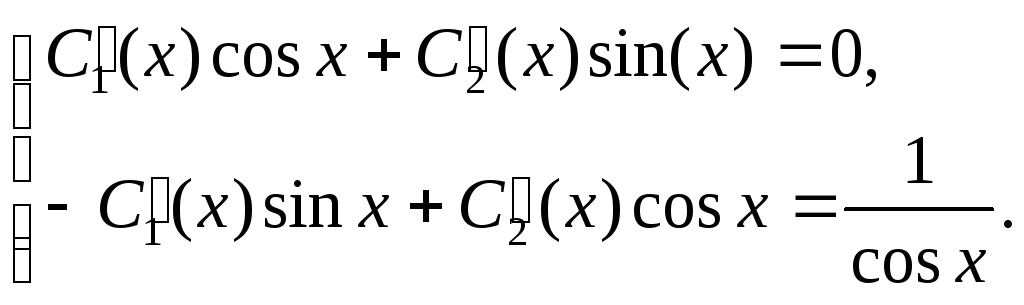Определитель
системы
По формулам Крамера получаем:
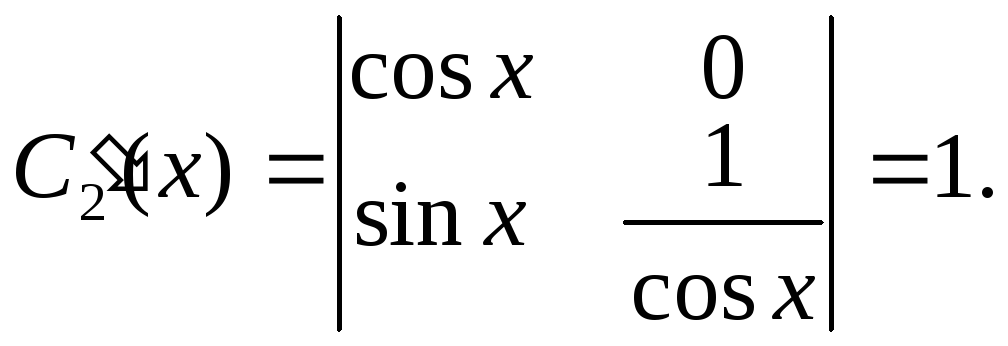
Отсюда
Подставляя
найденные функции в
,
получим общее решение нашего уравнения:
Задания для самостоятельного решения
Решить линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами:
1.
2.
3.
4.
5.
6.
Решить задачу Коши для линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
7.
8.
9.
10.
11.
12.
13.
14.
Решить линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами:
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
