
- •7. Определённый интеграл Понятие определённого интеграла
- •Интегрирование по частям в определённом интеграле
- •Вычисление площадей плоских фигур
- •Вычисление объёмов тел вращения
- •Несобственные интегралы
- •8. Числовые ряды
- •Свойства сходящихся рядов
- •Необходимый признак сходимости
- •Ряды с положительными членами. Признаки сходимости
- •Знакочередующиеся числовые ряды
- •Знакопеременные ряды
- •9. Степенные ряды
- •Область сходимости степенного ряда
- •Свойства степенных рядов
- •Ряд Маклорена
- •Применение рядов в приближённых вычислениях
- •10. Функции нескольких переменных
- •Предел и непрерывность
- •Частные производные
- •Дифференциал функции
- •Градиент
- •Производная по направлению
- •Частные производные высших порядков
- •11. Исследование функции нескольких переменных Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции двух переменных
- •Условный экстремум
- •Метод множителей Лагранжа
- •12. Общие понятия теории дифференциальных уравнений. Дифференциальные уравнения 1-го порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения
- •Уравнения в полных дифференциалах
- •13. Дифференциальные уравнения высших порядков Основные понятия и определения
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Метод вариации произвольных постоянных
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Если
правая часть линейного неоднородного
дифференциального уравнения с постоянными
коэффициентами
![]() имеет специальный вид
имеет специальный вид
![]() где
где
![]() -
многочлен n-й
степени, или
-
многочлен n-й
степени, или
![]() ,
или в общем случае
,
или в общем случае
![]() где
где
![]() - многочлен
- многочлен
m-й степени, то частное решение уравнения можно найти методом неопределенных коэффициентов.
Частное
решение ищут в похожем на f(x)
виде с неизвестными пока коэффициентами,
умножая в некоторых случаях на x
или на
![]()
Пример
14. Решить
уравнение
![]()
Решение.
Общее решение соответствующего
однородного уравнения имеет вид
![]() (см. пример 9).
(см. пример 9).
Общее
решение данного неоднородного уравнения
имеет вид
![]() где
где
![]() - частное решение неоднородного уравнения.
Частное решение
- частное решение неоднородного уравнения.
Частное решение
![]() будем искать в виде
будем искать в виде
![]() .
Найдем
.
Найдем
![]() ,
,
![]() подставим их в данное уравнение вместе
с
подставим их в данное уравнение вместе
с
![]() и определим коэффициент A.
и определим коэффициент A.
![]()
![]() ,
,
![]()
![]() 5A
= 10, A
= 2.
Итак,
5A
= 10, A
= 2.
Итак,
![]() -
частное решение данного уравнения.
Общее решение уравнения имеет вид
-
частное решение данного уравнения.
Общее решение уравнения имеет вид
![]()
Пример
15. Решить
уравнение
![]()
Решение.
Характеристическое уравнение
![]() имеет единственный корень k=1
кратности 2. Значит, частными решениями
соответствующего однородного уравнения
будут функции
имеет единственный корень k=1
кратности 2. Значит, частными решениями
соответствующего однородного уравнения
будут функции
![]() и
и
![]() ,
при подстановке которых в левую часть
уравнения вместе с их производными
правая часть уравнения обратится в
нуль. Поэтому частное решение неоднородного
уравнения будем искать в виде
,
при подстановке которых в левую часть
уравнения вместе с их производными
правая часть уравнения обратится в
нуль. Поэтому частное решение неоднородного
уравнения будем искать в виде
![]() Найдем
Найдем
![]() ,
,
![]() ,
подставим их в данное уравнение и
определим коэффициент A:
,
подставим их в данное уравнение и
определим коэффициент A:
![]()
![]() Отсюда
2A
= 1,
Отсюда
2A
= 1,
![]()
Итак,
![]() -
частное решение данного уравнения.
Тогда общее решение будет иметь вид:
-
частное решение данного уравнения.
Тогда общее решение будет иметь вид:
![]()
Пример
16. Решить
уравнение
![]()
Решение.
Общее решение однородного уравнения
![]() найдено в примере 13. Так как правая часть
данного уравнения
найдено в примере 13. Так как правая часть
данного уравнения
![]() является многочленом второй степени,
то и частное решение неоднородного
уравнения ищем в виде многочлена второй
степени
является многочленом второй степени,
то и частное решение неоднородного
уравнения ищем в виде многочлена второй
степени
![]() Находим
Находим
![]()
![]() , подставляем их в уравнение и определяем
коэффициенты A,
B,
C
:
, подставляем их в уравнение и определяем
коэффициенты A,
B,
C
:
или
![]()
Приравниваем
коэффициенты при одинаковых степенях
x
в правой и левой частях последнего
равенства:

Отсюда
находим A
= 1, B
=0,
![]() Следовательно,
Следовательно,
![]() - частное решение данного уравнения.
Тогда общее решение будет иметь вид:
- частное решение данного уравнения.
Тогда общее решение будет иметь вид:
![]()
Пример
17. Решить
уравнение
![]()
Решение.
Характеристическое уравнение
![]() соответствующего однородного уравнения
соответствующего однородного уравнения
![]() имеет корни
имеет корни
![]()
![]() Общее решение однородного уравнения
имеет вид
Общее решение однородного уравнения
имеет вид
![]() Так как уравнение не содержит искомой
функции y
а, значит, при дифференцировании степень
многочлена понизится на единицу, то
частное решение неоднородного уравнения
будем искать в виде
Так как уравнение не содержит искомой
функции y
а, значит, при дифференцировании степень
многочлена понизится на единицу, то
частное решение неоднородного уравнения
будем искать в виде
![]() .
.
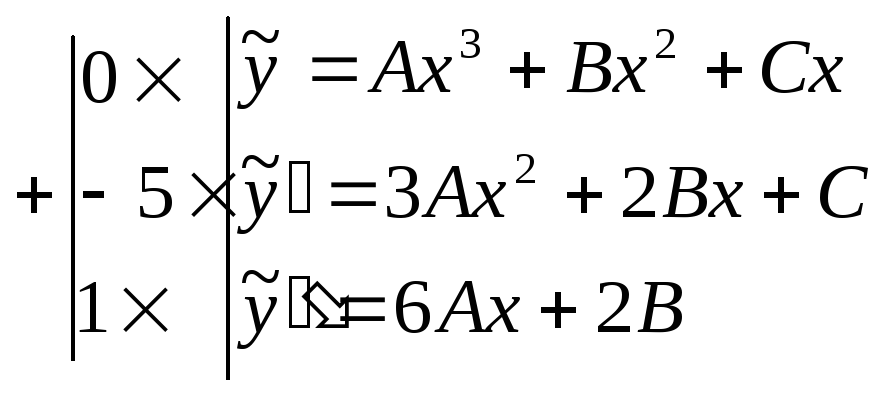
![]()
или
![]()
Приравнивая коэффициенты при одинаковых степенях x в правой и левой частях последнего равенства, получим систему для нахождения A, B, C:
 Отсюда
Отсюда
![]()
![]() -
частное решение данного уравнения.
-
частное решение данного уравнения.
Общее
решение имеет вид:
![]()
Пример
18. Решить
уравнение
![]()
Решение.
Характеристическое уравнение
![]() не имеет действительных корней.
не имеет действительных корней.
![]()
![]() Общее решение однородного уравнения
имеет вид
Общее решение однородного уравнения
имеет вид
![]()
Частное
решение неоднородного уравнения ищем
в виде
![]() Подставляя
Подставляя
![]() ,
,
![]() и
и
![]() в уравнение, находим коэффициенты A
и B
.
в уравнение, находим коэффициенты A
и B
.

![]()
Приравнивая
коэффициенты перед
![]() и
и
![]() в правой и левой частях равенства,
получим
в правой и левой частях равенства,
получим
 Отсюда
A
= 39, B
= 26.
Следовательно,
Отсюда
A
= 39, B
= 26.
Следовательно,
![]() - частное решение неоднородного уравнения.
Значит,
- частное решение неоднородного уравнения.
Значит,
![]() - общее решение данного уравнения.
- общее решение данного уравнения.
