7.7.4. Зонування території за допомогою полігонів Тиссена-Вороного
Полігонами Тиссена-Вороного називаються багатокутники, побудовані навколо мережі точкових об'єктів таким чином, що для будь-якої позиції в межах полігонів відстань до центрального точкового об'єкта завжди менша, ніж до будь-якого іншого об'єкта мережі, що розглядається.
Побудова багатокутників (полігонів) Тиссена-Вороного на практиці є однією з основних операцій, що поділяють територію, яка розглядається, на сукупність районів, що визначають просторові асоціації і взаємодії. Цей вид аналізу широко використовується для розподілу поверхні на основі визначених користувачем критеріїв і атрибутів.
Як приклад можна навести завдання визначення ареалів поширення даних спостережень на мережі метеорологічних станцій, нерівномірно розміщених у межах розглянутої території (рис. 7.6).
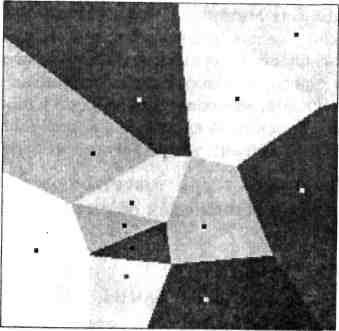
Рис. 7.6. Полігони Тиссена-Вороного, побудовані для нерівномірної мережі точкових об'єктів
Побудова полігонів Тиссена-Вороного є також основою одного з локально-детермінованих методів просторової інтерполяції точкових даних (див. п. 8.3.2). При цьому значення змінної в кожному вузлі мережі (наприклад, шар атмосферних опадів за даними спостережень метеорологічної станції) поширюються на всі комірки полігона, що оточує вузол.
Безумовним достоїнством методу є його простота і доступність реалізації практично у всіх ГІС-пакетах з розвиненими аналітичними можливостями. Проте слід пам'ятати, що на побудованій з використанням цього методу карті просторового розподілу змінної, що вивчається, остання зазнає розриву безперервності на межах полігонів, що, як правило, суперечить дійсності. До того ж характер змодельованого просторового розподілу значною мірою залежить від просторового розміщення вузлів мережі. У зв'язку з цим метод рекомендується для інтерполяції точкових значень при: а) відносно невеликому діапазоні змін даної змінної, б) просторовій однорідності умов формування її поля.
7.8. Оверлейний аналіз
При представленні аналітичних можливостей ГІС серед інших звичайно називають і оверлейні операції, або оверлейний аналіз, хоча тлумачення цих термінів неоднозначне. Як правило, при цьому розуміють операції «накладення один на одного двох або більше шарів, в результаті якого утворюється графічна композиція, або графічний оверлей, вихідних шарів (graphic overlay) або один похідний шар, що містить композицію просторових об'єктів вихідних шарів; топологія цієї композиції і атрибути арифметично або логічно похідні від топології і значень атрибутів вихідних об'єктів в топологічному оверлеї (topological overlay)» (Баранов и др., 1997). Таким чином, до понять «оверлейні операції» і «оверлейний аналіз» в загальному випадку можуть бути віднесені будь-які операції, пов'язані з графічним або аналітичним «накладенням» двох або більше шарів даних. Проте, враховуючи, що для растрової моделі просторових даних і арифметичні, і логічні операції з двома і будь-якою іншою кількістю шарів просторових даних виконуються з використанням алгоритмів картографічної алгебри, наведених вище (п. 7.5) уявляється доцільним в даному розділі розглянути операції, пов'язані з графічним оверлеем векторних даних, заснованих на алгоритмах аналітичної геометрії. Фактично це операції аналізу географічного збігу і включення та їх похідні на основі векторної моделі просторових даних.
У сумісних оверлейних операціях можуть використовуватися різні типи просторових об'єктів: точкові, лінійні і полігональні. Наприклад, аналіз вартості прокладення кабелю через кілька різних ділянок передбачає операцію накладення карти траси кабелю (лінійні дані) на карту землекористування (полігональні дані). При цьому визначається довжина ділянки траси, що проходить через кожне землекористування, і залежно від типу ділянки визначається вартість прокладення. Можуть також аналізуватися перетини з іншими підземними комунікаціями, розміщеними на різній глибині, наявність додаткових споживачів та ін. Проте найчастіше спостерігаються накладення двох полігональних шарів.
Програмна реалізація векторних оверлейних алгоритмів досить складна і пов'язана з великими витратами машинного часу на пошук координат всіх перетинів і лінійних сегментів, що утворюють полігони. Аналіз перетину двох ліній — основна дія оверлейного аналізу. Багато алгоритмів ГІС для складних процесів часто містять декілька простих, що використовується, наприклад, у виробництві оверлея багатокутників (шляхом з'єднання і роз'єднання багатокутників у лінії).
У разі оверлея двох прямих ліній для знаходження точки перетину двох ліній, що проходять через точку з відомими координатами, може використовуватися такий алгоритм (Core Curriculum..., 1991).
Рівняння прямої, як відомо, має вигляд:
Спираючись на дві точки на прямій з координатами (х ', уг) і (х2; у2), кутовий коефіцієнт b може бути визначений виразом:
Наприклад, нехай лінія 1 з координатами кінцевих точок (4, 2) і (2; 0) перетинає лінію 2 з координатами (0; 4) і (4; 0). Тоді кутовий коефіцієнт b для лінії 1 відповідно до (7.2) дорівнює:
Тоді рівняння (7.1) для лінії 1 в точці (4; 2) матиме вигляд
2 = а + 4. Звідси а = -2 і загальне рівняння лінії 1 має вигляд:
у = -2 + х. (7.3)
Аналогічні міркування для лінії 2 приводять до рівняння:
у = 4 - х. (7.4)
Координата х точки перетину ліній 1 і 2 (х = 3) знаходиться з рівняння, одержаного шляхом прирівнювання правих частин рівнянь (7.3) і (7.4). Підстановка цього значення х у рівняння (7.3) або (7.4) дає ординату точки перетину -y=1. Таким чином, координати точки перетину ліній 1 і 2 - (3; 1).
Загальний розв'язок розглянутої задачі має такий вигляд. Дві прямі лінії, що описуються рівняннями
перетинаються в точці з координатами:
Проте цей алгоритм може давати збій у багатьох випадках, наприклад, якщо одна з ліній вертикальна (Ь = 0) або лінії паралельні. Для запобігання цьому в програму оверлейного аналізу повинні вводитися додаткові процедури перевірки.
На практиці найчастіше спостерігаються випадки аналізу перетину складних ліній, що складаються з безлічі прямих сегментів. Вони також можуть бути оброблені простим алгоритмом, що перевіряє кожний сегмент в одній лінії проти кожного сегмента в іншій. Кількість роботи, яку необхідно виконати, пропорційна кількості сегментів (лі х п2). Обсяг непродуктивної роботи, спрямованої на аналіз сегментів, що явно не перетинаються, може бути значно скорочений за рахунок введення в алгоритм елементів евристичного аналізу.
Одним з таких методів є метод мінімально прилеглого прямокутника. Розміри такого прямокутника визначаються мінімумом і максимумом X і Y координат лінії. Якщо мінімально прилеглі прямокутники двох ліній не перетинаються, то і лінії не можуть перетнутися. Якщо вони перетинаються, то знаходяться мінімально прилеглі прямокутники для кожного сегмента лінії, щоб виділити ті, що мають нагоду перетнутися.
При оверлеї багатокутників, якими звичайно представлені полігони, використовується ряд інших алгоритмів, вибір яких залежить від типу операції. Вирізування вікна, побудова буфера навколо об'єкта, створення нової топологічної структури полігонів — основні цілі оверлейних операцій для багатокутників. У цьому випадку більш ефективні структури типу «дуга-вузол», оскільки для дуги виконується тільки одна операція пошуку замість чотирьох-п'яти для багатокутників-блоків, і при цьому доступна більша кількість атрибутивної інформації.
Розглянемо приклад оверлея двох полігонів з атрибутивними ознаками 1 і А, зовнішній простір яких має ознаку 0 (Core Curriculum..., 1991).
Перший полігон обмежений дугами з координатами вершин у точках (0; 1) (0; 3) (2; 3) (2; 1),(0, 1). Атрибути дуг: правий полігон — 1, лівий полігон — 0. Другий полігон обмежений дугами, що проходять через точки (1; 0), (3; 0), (3; 2), (1; 2) (1; 0). Атрибути дуг: правий полігон — 0, лівий полігон — А.
Після того як всі перетини будуть знайдені, формуються шість нових дуг - три з дуг полігону 1 і три з дуг полігону А:
1. (0; 1)(0; 3)(2; 3)(2; 2)
2. (2;2)(2;1)(1;1)
3. (1; 1)(0; 1)
4. (1;0)(3;0)(3;2)(2;2)
5. (2; 2)(1; 2)(1;1)
6. (1; 1)(1; 0)
Генеруються чотири нові полігони, атрибутивні ознаки яких комбінують ознаки батьківських полігонів 1 і А: 00, А0, А1 і 01:
|
Дуга |
Правий полігон |
Лівий полігон |
|
1 |
А0 |
00 |
|
2 |
А1 |
01 |
|
3 |
А0 |
00 |
|
4 |
00 |
01 |
|
5 |
А0 |
А1 |
|
6 |
00 |
01 |
Інший приклад топологічного оверлея з використанням логічних операторів і генерацією похідної таблиці атрибутів наведений на рис. 7.7.
Рис. 7.7. Приклад оверлея двох полігональних шарів (а) і (б) з генерацією похідного картографічного шару (в) і пов'язаної з ним таблиці атрибутів (г)
Цифрова обробка оверлея полігонів дуже трудомістка і тому є найскладнішою операцією для векторних ГІС. Необхідність забезпечення топологічної точності генерації нових полігонів передбачає залучення додаткових процедур для пошуку і обробки специфічних для оверлею похибок. Прикладом такої ненавмисної похибки можуть бути оверлей лінії (дуги), що має однакове розміщення на двох аналізованих картах (річка, залізниця, адміністративна границя і т.ін.). Через похибки дигітизування, навіть які не перевищують технічні допуски пристрою введення, дві лінії матимуть дещо різні координати і кілька разів взаємно перетинатимуться. У результаті оверлею на межі може утворитися ланцюжок маленьких витягнутих «паразитних» полігонів, які згодом доведеться видаляти вручну.
Сучасні ГІС-пакети, що використовують оверлеї, передбачають можливість автоматичного видалення нестиковок у процесі роботи. Критерії для відбору полігонів, що видаляються в автоматичному режимі, можуть бути такі:
- розмір полігона, що генерується, менше заданої умови;
- форма полігона дуже вузька і витягнута;
- кількість дуг, що утворюють полігон, становить 2, що досить рідко спостерігається в реальних полігонів (звичайно 3-4 і більше);
- має місце регулярне чергування дуг у ланцюжку суміжних полігонів.