2.6. Парадокс остаточного времени

Пусть поток трамваев есть поток событий восстановления с функцией распределения интервалов между трамваями A(x). В случайный момент времени t человек приходит на остановку. Сколько в среднем времени ему ждать трамвая?

1. Первое решение Так как в среднем длина интервала времени между трамваями равна и человек приходит совершенно произвольно, то ему ждать в среднем a/2.

2. Второе решение Время ожидания трамвая – это время перескока, распределенное с функцией распределения , т.е. с плотностью вероятностей . Поэтому ждать ему в среднем

. (19)

Как видно, два решения дали два разных результата, причем второе решение дает большее среднее время ожидания, чем первое. Какой же результат верен?

Верен второй результат. Разгадка в том, что промежутки времени между приходами трамваев разные и приходя в произвольный момент времени человек с большей вероятностью попадает на более длинный промежуток времени между трамваями, чем на более короткий.

2.7. Основное свойство рекуррентных потоков

Определение. Стационарный поток восстановления называется рекуррен­тным.

Теорема Если поток восстановления является стационарным, то есть является рекуррентным и , то

. (20)

Доказательство.

1. Докажем, что если поток стационарен, то H(t) – линейная по t функция.

Так как поток стационарен, то величины N_t+s – N_s и N_t – N₀ распределены одинаково, тогда

H(t + s) = M{N_t+s} = M{ N_t+s – N_s + N_s – N₀} = M{ N_t+s – N_s} + M{N_s – N₀} =

= M{ N_t} + M{N_s} = H(t) + H(s).

Следовательно H(t) является линейной функцией вида

H(t) = kt,

а так как , то .

2. Возьмем уравнение для функции восстановления

и подставим туда H(t) = kt, где . Тогда

,

откуда

,

или, если заменить t = x,то

.

Таким образом рекуррентный поток определяется единственной функцией распределения A(x).

Следствие. Если , то процесс восстановления не может быть стационарным, то есть не является рекуррентным.

Частный случай. Найдем, при каких условиях выполняется соотношение. Тогда A₁(x) = A(x)

.

Дифференцируя по x, получим

.

Разделяя переменные

,

и интегрируя, получим

,

откуда A(x) = 1 – e^-λx и поток является пуассоновским потоком с постоянной интенсивностью λ.

Глава 3. Полумарковские процессы

Обобщением цепей Маркова с непрерывным временем являются полумарковские случайные процессы с дискретным множеством состояний, реализации которых, аналогично цепям Маркова, являются кусочно постоянными непрерывными справа функциями.

В этой главе будет дано определение полумарковского процесса, процесса марковского восстановления, полумарковской матрицы, определяющей такие процессы, вложенной цепи Маркова для полумарковского процесса, а также будут определены другие понятия, необходимые для рассмотрения полумарковских процессов. Достаточно детально будет рассмотрен метод дополнительных переменных для анализа процессов марковского восстановления и полумарковских процессов

3.1. Определение основных понятий теории полумарковских процессов

Рассмотрим двумерный марковский процесс {ξ(n),τ(n)} с дискретным временем n = 0,1,2,… Первая компонента ξ(n) процесса принимает значения из некоторого дискретного множества. Для определенности, будем полагать, что ξ(n) = 1,2,…. Вторая компонента τ(n) принимает неотрицательные значения из непрерывного множества.

Определение. Марковской переходной функцией F(ν,x;k,y) однородного двумерного марковского процесса {ξ(n),τ(n)} называется функция

. (1)

Будем рассматривать только такие двумерные случайные процессы {ξ(n),τ(n)}, для марковских переходных функций которых выполняются равенства

(2)

то есть условное распределение (1) не зависит от значений второй компоненты τ(n) рассматриваемого двумерного марковского процесса. В этом случае марковскую переходную функцию F(ν,x;k) будем обозначать

. (3)

Определение. Матрица A(x), элементами которой являются функции A_kv(x), определяемые равенством (3), называется полумарковской.

Определим последовательность моментов времени

t₁< t₂ <…< t_n < t_n+1<…

равенством

t_n+1 = t_n + τ(n+1).

Определение. Случайный процесс k(t) с дискретным множеством состояний и непрерывным временем t называется полумарковским, заданным полумарковской матрицей A(x), если для всех n выполняются равенства

k(t) = ξ(n), t_n ≤ t < t_n+1.

То есть, на каждом интервале времени [t_n,t_n+1), процесс k(t) принимает и сохраняет то значение, которое в начале этого интервала приняла первая компонента ξ(n) рассматриваемого двумерного марковского процесса{ξ(n), τ(n)}.

В силу свойства (2), первая компонента ξ(n) рассматриваемого марковского процесса также является марковским процессом, точнее цепью Маркова с дискретным временем и матрицей P вероятностей p_kv переходов за один шаг, определяемой равенством

P = A(∞).

Цепь ξ(n) для рассматриваемого полумарковского процесса k(t) называется вложенной цепью Маркова.

Вторая компонента τ(n) процесса {ξ(n),τ(n)} является немарковским процессом, а именно последовательностью зависимых случайных величин, но для ее элементов в силу равенства (3) можно определить условную функцию распределения

.

В стационарном режиме функционирования полумарковского процесса по формуле полной вероятности можно записать и безусловную функцию распределения F(x) времени пребывания процесса k(t) в каждом состоянии

,

где r(k) – стационарное распределение вероятностей значений вложенной цепи Маркова ξ(n), которое определяется системой

Определение. Если компоненты ξ(n) и τ(n) двумерного случайного процесса {ξ(n),τ(n)} условно независимы, то есть для элементов A_kv(x) полумарковской матрицы A(x) выполняются равенства

(4)

то полумарковский процесс k(t) называется процессом марковского восстановления.

Это название оправдано тем, что в классической теории восстановления рассматриваются самовосстанавливающиеся устройства в виде элемента с конечным сроком службы. Как только этот элемент отказывает (выходит из строя), его заменяют другим элементом, который рано или поздно заменяется следующим элементом, и так далее.

Пусть имеются элементы разных видов, которыми можно заменить отказавший элемент. Срок службы элемента вида k является случайной величиной с функцией распределения A_k(x). Заданы вероятности p_kv того, что если выходит из строя элемент вида k, то его заменяют элементом вида v. Процесс k(t), определяющий вид элемента работающего в момент времени t, является процессом марковского восстановления.

Предполагаемая модель является существенным обобщением классических моделей восстановления с элементами одного вида.

В силу равенства (4) для процессов марковского восстановления полумарковскую матрицу A(x) можно записать в виде произведения матриц

A(x) = D(x)P, (5)

где D(x) – диагональная матрица с элементами A_k(x) по главной диагонали.

В силу определения (3) элементы A_kv(x) полумарковской матрицы определяют условные двумерные распределения вероятностей, задание которых могут вызвать затруднения, поэтому достаточно полезной является следующая мультипликативная форма этих элементов

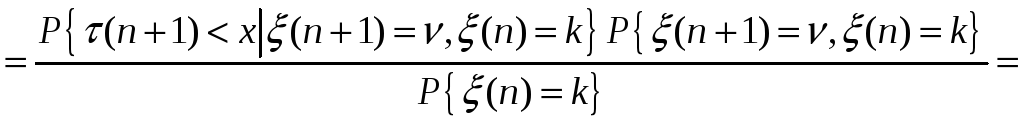
Таким образом, A_kv(x) можно записать в виде произведения

A_kv(x) = G_kv(x)p_kv (6)

где G_kv(x) – условная функция распределения времени пребывания полумарковского процесса в k-ом состоянии при условии, что переход будет осуществлен в состояние v.

Из равенства (6) следует, что полумарковскую матрицу можно записать в виде произведения Адамара

A(x) = G(x)*P

матриц G(x) и Р с элементами

Задание полумарковского процесса матрицами G(x) и Р гораздо проще, чем полумарковской матрицей A(x), но задание полумарковской матрицей более компактно.